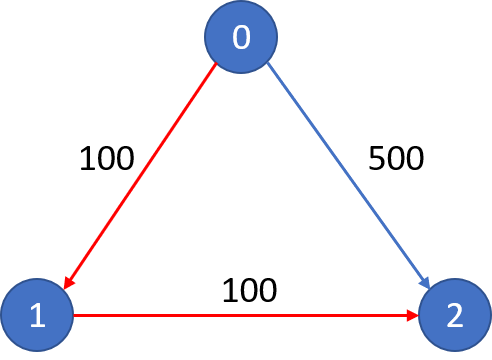
题目大意:有两种不同形状的骨牌(1×2长条形,L型)无限多块。给你一个2xN的板子,问一共有多少不同的方式可以完全覆盖。
We have two types of tiles: a 2×1 domino shape, and an “L” tromino shape. These shapes may be rotated.
|
1 2 3 4 |
XX <- domino XX <- "L" tromino X |
Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.
(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)
|
1 2 3 4 5 6 7 |
Example: Input: 3 Output: 5 Explanation: The five different ways are listed below, different letters indicates different tiles: XYZ XXZ XYY XXY XYY XYZ YYZ XZZ XYY XXY |
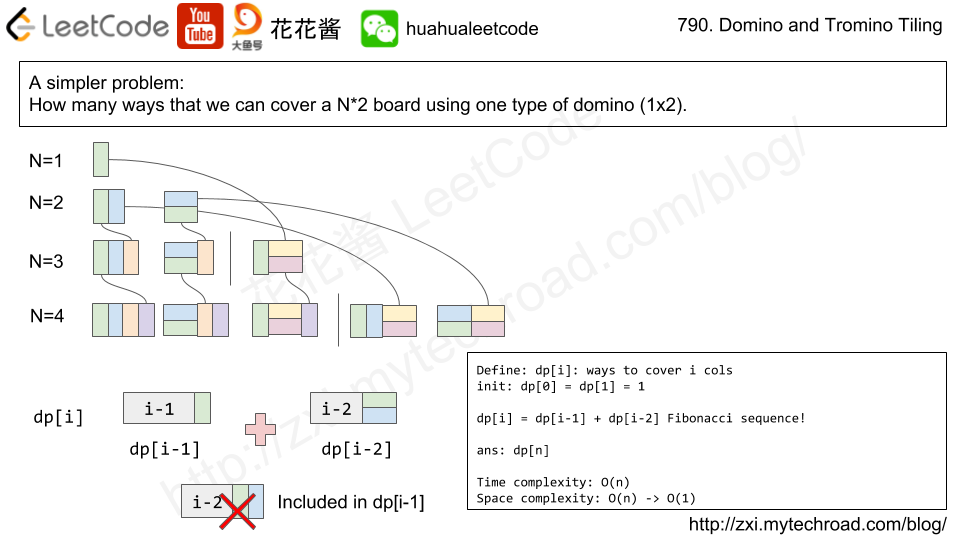
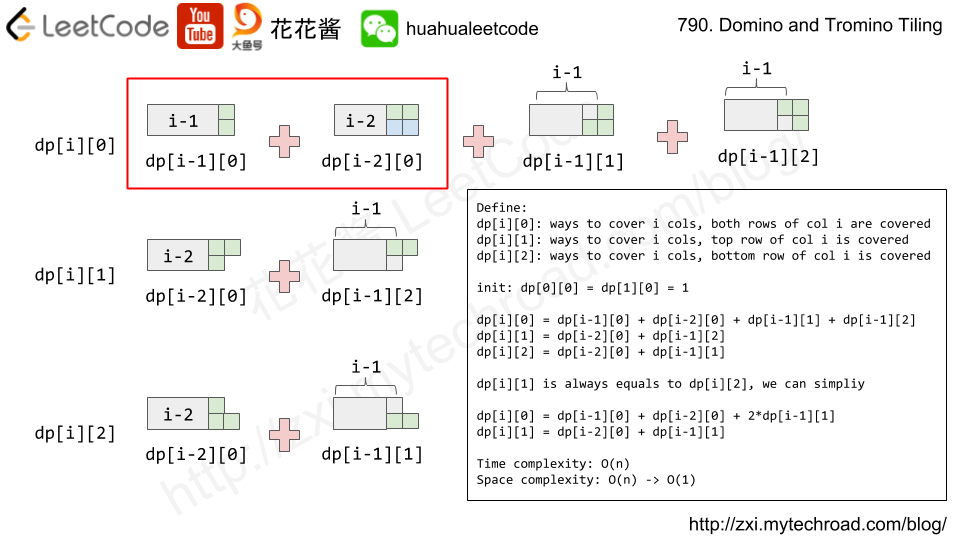
Idea: DP
dp[i][0]: ways to cover i cols, both rows of i-th col are covered
dp[i][1]: ways to cover i cols, only top row of i-th col is covered
dp[i][2]: ways to cover i cols, only bottom row of i-th col is covered
Solution 1: DP
Time complexity: O(N)
Space complexity: O(N)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
// Author: Huahua // Running time: 4 ms class Solution { public: int numTilings(int N) { constexpr int kMod = 1000000007; vector<vector<long>> dp(N + 1, vector<long>(3, 0)); dp[0][0] = dp[1][0] = 1; for (int i = 2; i <= N; ++i) { dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + dp[i - 1][1] + dp[i - 1][2]) % kMod; dp[i][1] = (dp[i - 2][0] + dp[i - 1][2]) % kMod; dp[i][2] = (dp[i - 2][0] + dp[i - 1][1]) % kMod; } return dp[N][0]; } }; |
C++ V2
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Since dp[i][1] always equals to dp[i][2], we can simplify a bit. // Author: Huahua // Running time: 4 ms class Solution { public: int numTilings(int N) { constexpr int kMod = 1000000007; vector<vector<long>> dp(N + 1, vector<long>(2, 0)); dp[0][0] = dp[1][0] = 1; for (int i = 2; i <= N; ++i) { dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + 2 * dp[i - 1][1]) % kMod; dp[i][1] = (dp[i - 2][0] + dp[i - 1][1]) % kMod; } return dp[N][0]; } }; |
Solution 2: DP
Another way to think about this problem
define: dp[i] ways to completely covert the i*2 board.
|
1 2 3 4 5 6 7 8 9 10 11 |
dp[0] = 1 # {} dp[1] = 1 # {|} dp[2] = 2 # {||, =} dp[3] = 5 # {|||, |=, =|, ⌊⌉, ⌈⌋} = dp[2] ⊗ {|} + dp[1] ⊗ {=} + dp[0] ⊗ {⌊⌉, ⌈⌋} dp[4] = 11 # dp[3] ⊗ {|} + dp[2] ⊗ {=} + dp[1] ⊗ {⌊⌉, ⌈⌋} + dp[0] ⊗ {⌊¯⌋,⌈_⌉} dp[5] = 24 # dp[4] ⊗ {|} + dp[3] ⊗ {=} + 2*(dp[2] + dp[1] + dp[0]) ... dp[n] = dp[n-1] + dp[n-2] + 2*(dp[n-3] + ... + dp[0]) = dp[n-1] + dp[n-3] + [dp[n-2] + dp[n-3] + 2*(dp[n-4] + ... + dp[0])] = dp[n-1] + dp[n-3] + dp[n-1] = 2*dp[n-1] + dp[n-3] |
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
// Author: Huahua // Running time: 3 ms class Solution { public: int numTilings(int N) { constexpr int kMod = 1000000007; vector<long> dp(N + 1, 1); dp[2] = 2; for (int i = 3; i <= N; ++i) dp[i] = (dp[i - 3] + dp[i - 1] * 2) % kMod; return dp[N]; } }; |