Posts published in May 2018

花花酱 LeetCode 334. Increasing Triplet Subsequence

By zxi on May 28, 2018

Problem

题目大意：判断一个数组中是否存在长度为3的单调递增子序列。

Formally the function should:

Return true if there exists i, j, k
such that arr[i] < arr[j] < arr[k] given 0 ≤ i < j < k ≤ n-1 else return false.

Your algorithm should run in O(n) time complexity and O(1) space complexity.

Examples:
Given [1, 2, 3, 4, 5],
return true.

Given [5, 4, 3, 2, 1],
return false.

Credits:
Special thanks to @DjangoUnchained for adding this problem and creating all test cases.

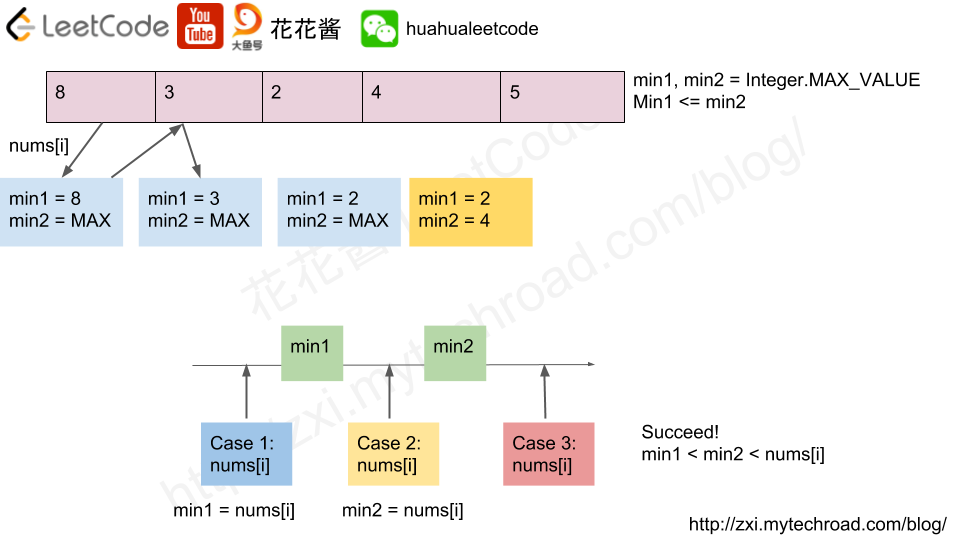
Solution: Greedy

Time complexity: O(n)

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 7 ms

class Solution {

public:

bool increasingTriplet(vector<int>& nums) {

int min1 = INT_MAX;

int min2 = INT_MAX;

for (int num : nums) {

if (num > min2) return true;

else if (num < min1) {

min1 = num;

} else if (num > min1 && num < min2) {

min2 = num;

}

return false;

}

};

花花酱 LeetCode 516. Longest Palindromic Subsequence

By zxi on May 28, 2018

Problem

题目大意：找出最长回文子序列的长度。

https://leetcode.com/problems/longest-palindromic-subsequence/description/

Given a string s, find the longest palindromic subsequence’s length in s. You may assume that the maximum length of s is 1000.

Example 1:
Input:

"bbbab"

Output:

One possible longest palindromic subsequence is “bbbb”.

Example 2:
Input:

"cbbd"

Output:

One possible longest palindromic subsequence is “bb”.

Solution: DP

Time complexity: O(n^2)

Space complexity: O(n^2)

C++

// Author: Huahua

// Running time: 102 ms

class Solution {

public:

int longestPalindromeSubseq(string s) {

const int n = s.length();

vector<vector<int>> dp(n, vector<int>(n, 0));

for (int l = 1; l <= n; ++l)

for (int i = 0; i <= n - l; ++i) {

int j = i + l - 1;

if (i == j) {

dp[i][j] = 1;

continue;

}

dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

if (s[i] == s[j])

dp[i][j] = dp[i + 1][j - 1] + 2;

}

return dp[0][n - 1];

}

};

Time complexity: O(n^2)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 28 ms

class Solution {

public:

int longestPalindromeSubseq(string s) {

const int n = s.length();

vector<int> dp0(n); // sols of len = l

vector<int> dp1(n); // sols of len = l - 1

vector<int> dp2(n); // sols of len = l - 2

for (int l = 1; l <= n; ++l) {

for (int i = 0; i <= n - l; ++i) {

int j = i + l - 1;

if (i == j) {

dp0[i] = 1;

continue;

}

if (s[i] == s[j])

dp0[i] = dp2[i + 1] + 2;

else

dp0[i] = max(dp1[i + 1], dp1[i]);

}

dp0.swap(dp1);

dp2.swap(dp0);

}

return dp1[0];

}

};

Python3

"""

Author: Huahua

Running time: 1276 ms

"""

class Solution:

def longestPalindromeSubseq(self, s):

n = len(s)

dp0 = [0] * n

dp1 = [1] * n

dp2 = [0] * n

for l in range(2, n + 1):

for i in range(0, n - l + 1):

j = i + l - 1

if s[i] == s[j]:

dp0[i] = dp2[i + 1] + 2

else:

dp0[i] = max(dp1[i + 1], dp1[i])

dp0, dp1, dp2 = dp2, dp0, dp1

return dp1[0]

// Author: Huahua

// Running time: 116 ms (beats 100%)

public class Solution {

public int LongestPalindromeSubseq(string s) {

var n = s.Length;

var dp0 = new int[n];

var dp1 = new int[n];

var dp2 = new int[n];

for (var l = 1; l <= n; ++l) {

for (var i = 0; i <= n - l; ++i) {

int j = i + l - 1;

if (i == j) {

dp0[i] = 1;

continue;

}

if (s[i] == s[j])

dp0[i] = dp2[i + 1] + 2;

else

dp0[i] = Math.Max(dp1[i], dp1[i + 1]);

}

var tmp = dp2;

dp2 = dp1;

dp1 = dp0;

dp0 = tmp;

}

return dp1[0];

}

花花酱 LeetCode 438. Find All Anagrams in a String

By zxi on May 28, 2018

Problem

题目大意：在s中找出所有p的Anagrams。

https://leetcode.com/problems/find-all-anagrams-in-a-string/description/

Given a string s and a non-empty string p, find all the start indices of p‘s anagrams in s.

Strings consists of lowercase English letters only and the length of both strings s and p will not be larger than 20,100.

The order of output does not matter.

Example 1:

Input:
s: "cbaebabacd" p: "abc"

Output:
[0, 6]

Explanation:
The substring with start index = 0 is "cba", which is an anagram of "abc".
The substring with start index = 6 is "bac", which is an anagram of "abc".

Example 2:

Input:
s: "abab" p: "ab"

Output:
[0, 1, 2]

Explanation:
The substring with start index = 0 is "ab", which is an anagram of "ab".
The substring with start index = 1 is "ba", which is an anagram of "ab".
The substring with start index = 2 is "ab", which is an anagram of "ab".

Solution: HashTable + Sliding Window

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 35 ms

class Solution {

public:

vector<int> findAnagrams(string s, string p) {

int n = s.length();

int l = p.length();

vector<int> ans;

vector<int> vp(26, 0);

vector<int> vs(26, 0);

for (char c : p) ++vp[c - 'a'];

for (int i = 0; i < n; ++i) {

if (i >= l) --vs[s[i - l] - 'a'];

++vs[s[i] - 'a'];

if (vs == vp) ans.push_back(i + 1 - l);

}

return ans;

}

};

花花酱 LeetCode 841. Keys and Rooms

By zxi on May 27, 2018

Problem

There are N rooms and you start in room 0. Each room has a distinct number in 0, 1, 2, ..., N-1, and each room may have some keys to access the next room.

Formally, each room i has a list of keys rooms[i], and each key rooms[i][j] is an integer in [0, 1, ..., N-1] where N = rooms.length. A key rooms[i][j] = v opens the room with number v.

Initially, all the rooms start locked (except for room 0).

You can walk back and forth between rooms freely.

Return true if and only if you can enter every room.

Example 1:

Input: [[1],[2],[3],[]]
Output: true
Explanation:  
We start in room 0, and pick up key 1.
We then go to room 1, and pick up key 2.
We then go to room 2, and pick up key 3.
We then go to room 3.  Since we were able to go to every room, we return true.

Example 2:

Input: [[1,3],[3,0,1],[2],[0]]
Output: false
Explanation: We can't enter the room with number 2.

Note:

1 <= rooms.length <= 1000
0 <= rooms[i].length <= 1000
The number of keys in all rooms combined is at most 3000.

Solution: DFS

Time complexity: O(V + E)

Space complexity: O(V)

C++

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

bool canVisitAllRooms(vector<vector<int>>& rooms) {

unordered_set<int> visited;

dfs(rooms, 0, visited);

return visited.size() == rooms.size();

}

private:

void dfs(const vector<vector<int>>& rooms,

int cur, unordered_set<int>& visited) {

if (visited.count(cur)) return;

visited.insert(cur);

for (int nxt : rooms[cur])

dfs(rooms, nxt, visited);

}

};

花花酱 LeetCode 329. Longest Increasing Path in a Matrix

By zxi on May 24, 2018

Problem

Given an integer matrix, find the length of the longest increasing path.

From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).

Example 1:

Input: nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
Output: 4 
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

Input: nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
] 
Output: 4 
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Solution1: DFS + Memorization

Time complexity: O(mn)

Space complexity: O(mn)

C++

// Author: Huahua

// Running time: 36 ms

class Solution {

public:

int longestIncreasingPath(vector<vector<int>>& matrix) {

if (matrix.empty()) return 0;

m_ = matrix.size();

n_ = matrix[0].size();

dp_ = vector<vector<int>>(m_, vector<int>(n_, -1));

int ans = 0;

for (int y = 0; y < m_; ++y)

for (int x = 0; x < n_; ++x)

ans = max(ans, dfs(matrix, x, y));

return ans;

}

private:

int dfs(const vector<vector<int>>& mat, int x, int y) {

if (dp_[y][x] != -1) return dp_[y][x];

static int dirs[] = {0, -1, 0, 1, 0};

dp_[y][x] = 1;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || ty < 0 || tx >= n_ || ty >= m_ || mat[ty][tx] <= mat[y][x])

continue;

dp_[y][x] = max(dp_[y][x], 1 + dfs(mat, tx, ty));

}

return dp_[y][x];

}

int m_;

int n_;

// dp[i][j]: max length start from (j, i)

vector<vector<int>> dp_;

};

Solution2: DP

Time complexity: O(mn*log(mn))

Space complexity: O(mn)

// Author: Huahua

// Running time: 63 ms

class Solution {

public:

int longestIncreasingPath(vector<vector<int>>& matrix) {

if (matrix.empty()) return 0;

int m = matrix.size();

int n = matrix[0].size();

vector<vector<int>> dp(m, vector<int>(n, 1));

int ans = 0;

vector<pair<int, pair<int, int>>> cells;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

cells.push_back({matrix[y][x], {x, y}});

sort(cells.rbegin(), cells.rend());

vector<int> dirs {0, 1, 0, -1, 0};

for (const auto& cell : cells) {

int x = cell.second.first;

int y = cell.second.second;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || tx >= n || ty < 0 || ty >= m) continue;

if (matrix[ty][tx] <= matrix[y][x]) continue;

dp[y][x] = max(dp[y][x], 1 + dp[ty][tx]);

}

ans = max(ans, dp[y][x]);

}

return ans;

}

};