You are given the root of a binary tree and a positive integer k.
The level sum in the tree is the sum of the values of the nodes that are on the same level.
Return the kth largest level sum in the tree (not necessarily distinct). If there are fewer than k levels in the tree, return -1.
Note that two nodes are on the same level if they have the same distance from the root.
Example 1:

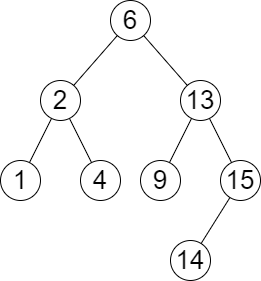
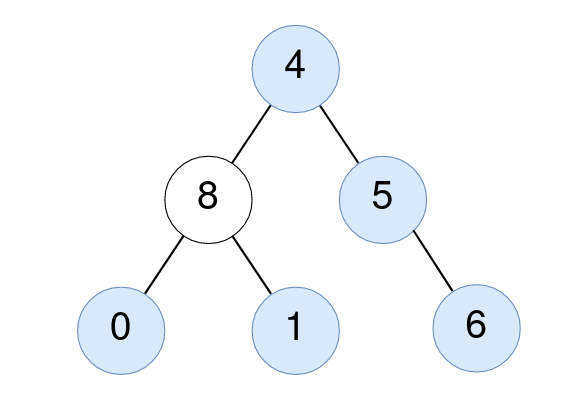
Input: root = [5,8,9,2,1,3,7,4,6], k = 2 Output: 13 Explanation: The level sums are the following: - Level 1: 5. - Level 2: 8 + 9 = 17. - Level 3: 2 + 1 + 3 + 7 = 13. - Level 4: 4 + 6 = 10. The 2nd largest level sum is 13.
Example 2:
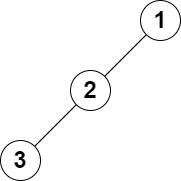
Input: root = [1,2,null,3], k = 1 Output: 3 Explanation: The largest level sum is 3.
Constraints:
- The number of nodes in the tree is
n. 2 <= n <= 1051 <= Node.val <= 1061 <= k <= n
Solution: DFS + Sorting
Use DFS to traverse the tree and accumulate level sum. Once done, sort the level sums and find the k-th largest one.
Time complexity: O(n)
Space complexity: O(n)
Note: sum can be very large, use long long.
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
// Author: Huahua class Solution { public: long long kthLargestLevelSum(TreeNode* root, int k) { vector<long long> sums; function<void(TreeNode*, int)> dfs = [&](TreeNode* root, int d) { if (!root) return; while (d >= sums.size()) sums.push_back(0); sums[d] += root->val; dfs(root->left, d + 1); dfs(root->right, d + 1); }; dfs(root, 0); if (sums.size() < k) return -1; sort(rbegin(sums), rend(sums)); return sums[k - 1]; } }; |