Posts tagged as “union find”

花花酱 LeetCode 1061. Lexicographically Smallest Equivalent String

By zxi on January 14, 2023

You are given two strings of the same length s1 and s2 and a string baseStr.

We say s1[i] and s2[i] are equivalent characters.

For example, if s1 = "abc" and s2 = "cde", then we have 'a' == 'c', 'b' == 'd', and 'c' == 'e'.

Equivalent characters follow the usual rules of any equivalence relation:

Reflexivity: 'a' == 'a'.
Symmetry: 'a' == 'b' implies 'b' == 'a'.
Transitivity: 'a' == 'b' and 'b' == 'c' implies 'a' == 'c'.

For example, given the equivalency information from s1 = "abc" and s2 = "cde", "acd" and "aab" are equivalent strings of baseStr = "eed", and "aab" is the lexicographically smallest equivalent string of baseStr.

Return the lexicographically smallest equivalent string of baseStr by using the equivalency information from s1 and s2.

Example 1:

Input: s1 = "parker", s2 = "morris", baseStr = "parser"
Output: "makkek"
Explanation: Based on the equivalency information in s1 and s2, we can group their characters as [m,p], [a,o], [k,r,s], [e,i].
The characters in each group are equivalent and sorted in lexicographical order.
So the answer is "makkek".

Example 2:

Input: s1 = "hello", s2 = "world", baseStr = "hold"
Output: "hdld"
Explanation: Based on the equivalency information in s1 and s2, we can group their characters as [h,w], [d,e,o], [l,r].
So only the second letter 'o' in baseStr is changed to 'd', the answer is "hdld".

Example 3:

Input: s1 = "leetcode", s2 = "programs", baseStr = "sourcecode"

Output: "aauaaaaada"

Explanation: We group the equivalent characters in s1 and s2 as [a,o,e,r,s,c], [l,p], [g,t] and [d,m], thus all letters in baseStr except 'u' and 'd' are transformed to 'a', the answer is "aauaaaaada".

Constraints:

1 <= s1.length, s2.length, baseStr <= 1000
s1.length == s2.length
s1, s2, and baseStr consist of lowercase English letters.

Solution: Union Find

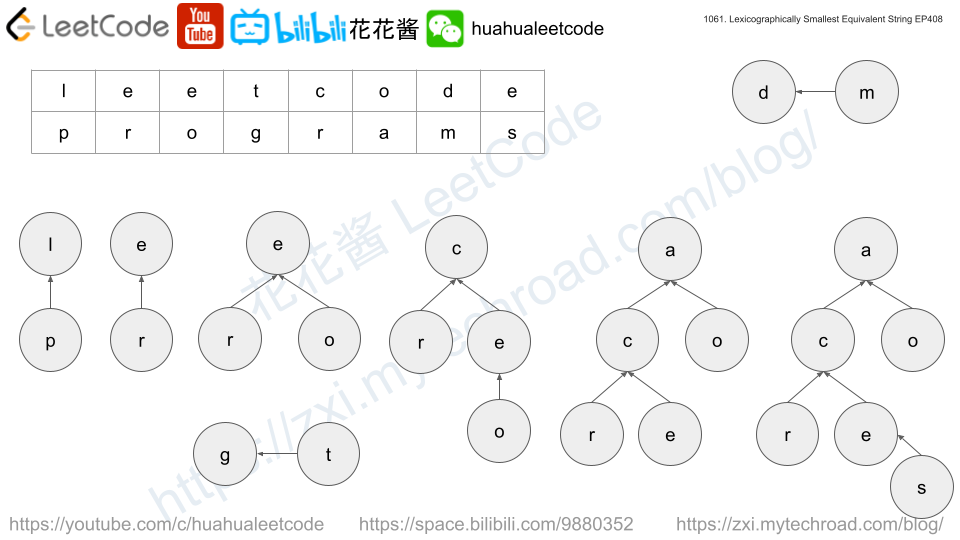
Time complexity: O(n + m)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

string smallestEquivalentString(string s1, string s2, string baseStr) {

vector<int> p(26);

iota(begin(p), end(p), 0);

function<int(int)> find = [&](int x) {

return p[x] == x ? x : p[x] = find(p[x]);

};

for (int i = 0; i < s1.length(); ++i) {

int r1 = find(s1[i] - 'a');

int r2 = find(s2[i] - 'a');

if (r2 < r1) swap(r1, r2);

p[r2] = r1;

}

string ans(baseStr);

for (int i = 0; i < baseStr.length(); ++i) {

ans[i] = find(baseStr[i] - 'a') + 'a';

}

return ans;

}

};

花花酱 LeetCode 2316. Count Unreachable Pairs of Nodes in an Undirected Graph

By zxi on June 25, 2022

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

Constraints:

1 <= n <= 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no repeated edges.

Solution 1: DFS

Use DFS to find all CCs

Time complexity: O(V+E)
Space complexity: O(V+E)

C++

// Author: Huahua

// Author: Huahua, 791ms, 136 MB

class Solution {

public:

long long countPairs(int n, vector<vector<int>>& edges) {

vector<vector<int>> g(n);

for (const auto& e : edges) {

g[e[0]].push_back(e[1]);

g[e[1]].push_back(e[0]);

}

vector<int> seen(n);

long long cur = 0;

function<void(int)> dfs = [&](int u) {

++cur;

for (int v : g[u])

if (seen[v]++ == 0) dfs(v);

};

long long ans = 0;

for (int i = 0; i < n; ++i) {

if (seen[i]++) continue;

cur = 0;

dfs(i);

ans += (n - cur) * cur;

}

return ans / 2;

}

};

Solution 2: Union Find

Time complexity: O(V+E)
Space complexity: O(V)

C++

// Author: Huahua

class Solution {

public:

long long countPairs(int n, vector<vector<int>>& edges) {

vector<int> parents(n);

vector<int> counts(n, 1);

std::iota(begin(parents), end(parents), 0);

function<int(int)> find = [&](int x) {

if (parents[x] == x) return x;

return parents[x] = find(parents[x]);

};

for (const auto& e : edges) {

int ru = find(e[0]);

int rv = find(e[1]);

if (ru != rv) {

parents[rv] = ru;

counts[ru] += counts[rv];

}

long long ans = 0;

for (int i = 0; i < n; ++i)

ans += n - counts[find(i)];

return ans / 2;

}

};

花花酱 LeetCode 2157. Groups of Strings

By zxi on February 6, 2022

You are given a 0-indexed array of strings words. Each string consists of lowercase English letters only. No letter occurs more than once in any string of words.

Two strings s1 and s2 are said to be connected if the set of letters of s2 can be obtained from the set of letters of s1 by any one of the following operations:

Adding exactly one letter to the set of the letters of s1.
Deleting exactly one letter from the set of the letters of s1.
Replacing exactly one letter from the set of the letters of s1 with any letter, including itself.

The array words can be divided into one or more non-intersecting groups. A string belongs to a group if any one of the following is true:

It is connected to at least one other string of the group.
It is the only string present in the group.

Note that the strings in words should be grouped in such a manner that a string belonging to a group cannot be connected to a string present in any other group. It can be proved that such an arrangement is always unique.

Return an array ans of size 2 where:

ans[0] is the total number of groups words can be divided into, and
ans[1] is the size of the largest group.

Example 1:

Input: words = ["a","b","ab","cde"]
Output: [2,3]
Explanation:
- words[0] can be used to obtain words[1] (by replacing 'a' with 'b'), and words[2] (by adding 'b'). So words[0] is connected to words[1] and words[2].
- words[1] can be used to obtain words[0] (by replacing 'b' with 'a'), and words[2] (by adding 'a'). So words[1] is connected to words[0] and words[2].
- words[2] can be used to obtain words[0] (by deleting 'b'), and words[1] (by deleting 'a'). So words[2] is connected to words[0] and words[1].
- words[3] is not connected to any string in words.
Thus, words can be divided into 2 groups ["a","b","ab"] and ["cde"]. The size of the largest group is 3.

Example 2:

Input: words = ["a","ab","abc"]
Output: [1,3]
Explanation:
- words[0] is connected to words[1].
- words[1] is connected to words[0] and words[2].
- words[2] is connected to words[1].
Since all strings are connected to each other, they should be grouped together.
Thus, the size of the largest group is 3.

Constraints:

1 <= words.length <= 2 * 10⁴
1 <= words[i].length <= 26
words[i] consists of lowercase English letters only.
No letter occurs more than once in words[i].

Solution: Bitmask + DFS

Use a bitmask to represent a string. Use dfs to find connected components.

Time complexity: O(n*26²)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> groupStrings(vector<string>& words) {

unordered_map<int, int> m;

for (const string& w : words)

++m[accumulate(begin(w), end(w), 0, [](int k, char c){ return k | (1 << (c - 'a')); })];

function<int(int)> dfs = [&](int mask) {

auto it = m.find(mask);

if (it == end(m)) return 0;

int ans = it->second;

m.erase(it);

for (int i = 0; i < 26; ++i) {

ans += dfs(mask ^ (1 << i));

for (int j = i + 1; j < 26; ++j)

if ((mask >> i & 1) != (mask >> j & 1))

ans += dfs(mask ^ (1 << i) ^ (1 << j));

}

return ans;

};

int size = 0;

int groups = 0;

while (!m.empty()) {

size = max(size, dfs(begin(m)->first));

++groups;

}

return {groups, size};

}

};

花花酱 LeetCode 1998. GCD Sort of an Array

By zxi on December 31, 2021

You are given an integer array nums, and you can perform the following operation any number of times on nums:

Swap the positions of two elements nums[i] and nums[j] if gcd(nums[i], nums[j]) > 1 where gcd(nums[i], nums[j]) is the greatest common divisor of nums[i] and nums[j].

Return true if it is possible to sort nums in non-decreasing order using the above swap method, or false otherwise.

Example 1:

Input: nums = [7,21,3]
Output: true
Explanation: We can sort [7,21,3] by performing the following operations:
- Swap 7 and 21 because gcd(7,21) = 7. nums = [21,7,3]
- Swap 21 and 3 because gcd(21,3) = 3. nums = [3,7,21]

Example 2:

Input: nums = [5,2,6,2]
Output: false
Explanation: It is impossible to sort the array because 5 cannot be swapped with any other element.

Example 3:

Input: nums = [10,5,9,3,15]
Output: true
We can sort [10,5,9,3,15] by performing the following operations:
- Swap 10 and 15 because gcd(10,15) = 5. nums = [15,5,9,3,10]
- Swap 15 and 3 because gcd(15,3) = 3. nums = [3,5,9,15,10]
- Swap 10 and 15 because gcd(10,15) = 5. nums = [3,5,9,10,15]

Constraints:

1 <= nums.length <= 3 * 10⁴
2 <= nums[i] <= 10⁵

Solution: Union-Find

Let nums[j]’s target position be i. In order to put nums[j] to pos i by swapping. nums[i] and nums[j] must be in the same connected component. There is an edge between two numbers if they have gcd > 1.

We union two numbers if their have gcd > 1. However, it will be TLE if we do all pairs . Thus, for each number, we union it with its divisors instead.

Time complexity: O(n²) TLE -> O(sum(sqrt(nums[i]))) <= O(n*sqrt(m))
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

bool gcdSort(vector<int>& nums) {

const int m = *max_element(begin(nums), end(nums));

const int n = nums.size();

vector<int> p(m + 1);

iota(begin(p), end(p), 0);

function<int(int)> find = [&](int x) {

return p[x] == x ? x : (p[x] = find(p[x]));

};

for (int x : nums)

for (int d = 2; d <= sqrt(x); ++d)

if (x % d == 0)

p[find(x)] = p[find(x / d)] = find(d);

vector<int> sorted(nums);

sort(begin(sorted), end(sorted));

for (int i = 0; i < n; ++i)

if (find(sorted[i]) != find(nums[i]))

return false;

return true;

}

};

花花酱 LeetCode 2092. Find All People With Secret

By zxi on November 28, 2021

You are given an integer n indicating there are n people numbered from 0 to n - 1. You are also given a 0-indexed 2D integer array meetings where meetings[i] = [x_i, y_i, time_i] indicates that person x_i and person y_i have a meeting at time_i. A person may attend multiple meetings at the same time. Finally, you are given an integer firstPerson.

Person 0 has a secret and initially shares the secret with a person firstPerson at time 0. This secret is then shared every time a meeting takes place with a person that has the secret. More formally, for every meeting, if a person x_i has the secret at time_i, then they will share the secret with person y_i, and vice versa.

The secrets are shared instantaneously. That is, a person may receive the secret and share it with people in other meetings within the same time frame.

Return a list of all the people that have the secret after all the meetings have taken place. You may return the answer in any order.

Example 1:

Input: n = 6, meetings = [[1,2,5],[2,3,8],[1,5,10]], firstPerson = 1
Output: [0,1,2,3,5]
Explanation:
At time 0, person 0 shares the secret with person 1.
At time 5, person 1 shares the secret with person 2.
At time 8, person 2 shares the secret with person 3.
At time 10, person 1 shares the secret with person 5.
Thus, people 0, 1, 2, 3, and 5 know the secret after all the meetings.

Example 2:

Input: n = 4, meetings = [[3,1,3],[1,2,2],[0,3,3]], firstPerson = 3
Output: [0,1,3]
Explanation:
At time 0, person 0 shares the secret with person 3.
At time 2, neither person 1 nor person 2 know the secret.
At time 3, person 3 shares the secret with person 0 and person 1.
Thus, people 0, 1, and 3 know the secret after all the meetings.

Example 3:

Input: n = 5, meetings = [[3,4,2],[1,2,1],[2,3,1]], firstPerson = 1
Output: [0,1,2,3,4]
Explanation:
At time 0, person 0 shares the secret with person 1.
At time 1, person 1 shares the secret with person 2, and person 2 shares the secret with person 3.
Note that person 2 can share the secret at the same time as receiving it.
At time 2, person 3 shares the secret with person 4.
Thus, people 0, 1, 2, 3, and 4 know the secret after all the meetings.

Example 4:

Input: n = 6, meetings = [[0,2,1],[1,3,1],[4,5,1]], firstPerson = 1
Output: [0,1,2,3]
Explanation:
At time 0, person 0 shares the secret with person 1.
At time 1, person 0 shares the secret with person 2, and person 1 shares the secret with person 3.
Thus, people 0, 1, 2, and 3 know the secret after all the meetings.

Constraints:

2 <= n <= 10⁵
1 <= meetings.length <= 10⁵
meetings[i].length == 3
0 <= x_i, y_i<= n - 1
x_i != y_i
1 <= time_i <= 10⁵
1 <= firstPerson <= n - 1

Solution: Union Find

Sorting meetings by time.

At each time stamp, union people who meet.
Key step: “un-union” people if they DO NOT connected to 0 / known the secret after each timestamp.

Time complexity: O(nlogn + m + n)
Space complexity: O(m + n)

C++

// Author: Huahua

class Solution {

public:

vector<int> findAllPeople(int n, vector<vector<int>>& meetings, int firstPerson) {

map<int, vector<pair<int, int>>> events;

for (const auto& m : meetings)

events[m[2]].emplace_back(m[0], m[1]);

vector<int> p(n);

iota(begin(p), end(p), 0);

function<int(int)> find = [&](int x) {

return p[x] == x ? x : (p[x] = find(p[x]));

};

p[firstPerson] = 0;

for (const auto& [t, s] : events) {

for (const auto [u, v] : s)

p[find(u)] = find(v);

for (const auto [u, v] : s) {

if (find(u) != find(0)) p[u] = u;

if (find(v) != find(0)) p[v] = v;

}

vector<int> ans;

for (int i = 0; i < n; ++i)

if (find(i) == find(0)) ans.push_back(i);

return ans;

}

};

Posts tagged as “union find”

花花酱 LeetCode 1061. Lexicographically Smallest Equivalent String

Solution: Union Find

C++

花花酱 LeetCode 2316. Count Unreachable Pairs of Nodes in an Undirected Graph

Solution 1: DFS

C++

Solution 2: Union Find

C++

花花酱 LeetCode 2157. Groups of Strings

Solution: Bitmask + DFS

C++

花花酱 LeetCode 1998. GCD Sort of an Array

Solution: Union-Find

C++

花花酱 LeetCode 2092. Find All People With Secret

Solution: Union Find

C++

Related Problems