Posts tagged as “DFS”

花花酱 LeetCode 2658. Maximum Number of Fish in a Grid

By zxi on April 30, 2023

You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:

A land cell if grid[r][c] = 0, or
A water cell containing grid[r][c] fish, if grid[r][c] > 0.

A fisher can start at any water cell (r, c) and can do the following operations any number of times:

Catch all the fish at cell (r, c), or
Move to any adjacent water cell.

Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.

An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.

Example 1:

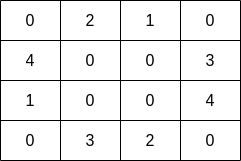
Input: grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
Output: 7
Explanation: The fisher can start at cell (1,3) and collect 3 fish, then move to cell (2,3) and collect 4 fish.

Example 2:

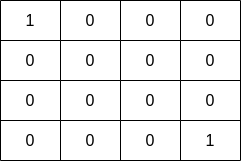
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
Output: 1
Explanation: The fisher can start at cells (0,0) or (3,3) and collect a single fish.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10
0 <= grid[i][j] <= 10

Solution: Connected Component

Find the connected component that has the max sum.

Time complexity: O(mn)
Space complexity: O(mn)

C++

// Author: Huahua

class Solution {

public:

int findMaxFish(vector<vector<int>>& grid) {

const int m = grid.size();

const int n = grid[0].size();

function<int(int, int)> dfs = [&](int r, int c) {

if (r < 0 || r >= m || c < 0 || c >= n || !grid[r][c]) return 0;

return exchange(grid[r][c], 0)

+ dfs(r - 1, c) + dfs(r, c - 1) + dfs(r + 1, c) + dfs(r, c + 1);

};

int ans = 0;

for (int r = 0; r < m; ++r)

for (int c = 0; c < n; ++c)

ans = max(ans, dfs(r, c));

return ans;

}

};

花花酱 LeetCode 2583. Kth Largest Sum in a Binary Tree

By zxi on March 5, 2023

You are given the root of a binary tree and a positive integer k.

The level sum in the tree is the sum of the values of the nodes that are on the same level.

Return the k^th largest level sum in the tree (not necessarily distinct). If there are fewer than k levels in the tree, return -1.

Note that two nodes are on the same level if they have the same distance from the root.

Example 1:

Input: root = [5,8,9,2,1,3,7,4,6], k = 2
Output: 13
Explanation: The level sums are the following:
- Level 1: 5.
- Level 2: 8 + 9 = 17.
- Level 3: 2 + 1 + 3 + 7 = 13.
- Level 4: 4 + 6 = 10.
The 2^nd largest level sum is 13.

Example 2:

Input: root = [1,2,null,3], k = 1
Output: 3
Explanation: The largest level sum is 3.

Constraints:

The number of nodes in the tree is n.
2 <= n <= 10⁵
1 <= Node.val <= 10⁶
1 <= k <= n

Solution: DFS + Sorting

Use DFS to traverse the tree and accumulate level sum. Once done, sort the level sums and find the k-th largest one.

Time complexity: O(n)
Space complexity: O(n)

Note: sum can be very large, use long long.

C++

// Author: Huahua

class Solution {

public:

long long kthLargestLevelSum(TreeNode* root, int k) {

vector<long long> sums;

function<void(TreeNode*, int)> dfs = [&](TreeNode* root, int d) {

if (!root) return;

while (d >= sums.size()) sums.push_back(0);

sums[d] += root->val;

dfs(root->left, d + 1);

dfs(root->right, d + 1);

};

dfs(root, 0);

if (sums.size() < k) return -1;

sort(rbegin(sums), rend(sums));

return sums[k - 1];

}

};

花花酱 LeetCode 2477. Minimum Fuel Cost to Report to the Capital

By zxi on November 26, 2022

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [a_i, b_i] denotes that there exists a bidirectional road connecting cities a_i and b_i.

There is a meeting for the representatives of each city. The meeting is in the capital city.

There is a car in each city. You are given an integer seats that indicates the number of seats in each car.

A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.

Return the minimum number of liters of fuel to reach the capital city.

Example 1:

Input: roads = [[0,1],[0,2],[0,3]], seats = 5
Output: 3
Explanation: 
- Representative₁ goes directly to the capital with 1 liter of fuel.
- Representative₂ goes directly to the capital with 1 liter of fuel.
- Representative₃ goes directly to the capital with 1 liter of fuel.
It costs 3 liters of fuel at minimum. 
It can be proven that 3 is the minimum number of liters of fuel needed.

Example 2:

Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
Output: 7
Explanation: 
- Representative₂ goes directly to city 3 with 1 liter of fuel.
- Representative₂ and representative₃ go together to city 1 with 1 liter of fuel.
- Representative₂ and representative₃ go together to the capital with 1 liter of fuel.
- Representative₁ goes directly to the capital with 1 liter of fuel.
- Representative₅ goes directly to the capital with 1 liter of fuel.
- Representative₆ goes directly to city 4 with 1 liter of fuel.
- Representative₄ and representative₆ go together to the capital with 1 liter of fuel.
It costs 7 liters of fuel at minimum. 
It can be proven that 7 is the minimum number of liters of fuel needed.

Example 3:

Input: roads = [], seats = 1
Output: 0
Explanation: No representatives need to travel to the capital city.

Constraints:

1 <= n <= 10⁵
roads.length == n - 1
roads[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
roads represents a valid tree.
1 <= seats <= 10⁵

Solution: Greedy + DFS

To reach the minimum cost, we must share cars if possible, say X reps from children nodes to an intermediate node u on the way towards capital 0. Then they all changes cars at node u, and we need (X + 1) // seats cars/fuel from u to 0.

We use DFS to count # of reps at each node u while accumulating the total cost.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

long long minimumFuelCost(vector<vector<int>>& roads, int seats) {

long long ans = 0;

vector<vector<int>> g(roads.size() + 1);

for (const vector<int>& r : roads) {

g[r[0]].push_back(r[1]);

g[r[1]].push_back(r[0]);

}

// Returns total # of children of u.

function<int(int, int)> dfs = [&](int u, int p, int rep = 1) {

for (int v : g[u])

if (v != p) rep += dfs(v, u);

if (u) ans += (rep + seats - 1) / seats;

return rep;

};

dfs(0, -1);

return ans;

}

};

花花酱 LeetCode 2316. Count Unreachable Pairs of Nodes in an Undirected Graph

By zxi on June 25, 2022

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

Constraints:

1 <= n <= 10⁵
0 <= edges.length <= 2 * 10⁵
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no repeated edges.

Solution 1: DFS

Use DFS to find all CCs

Time complexity: O(V+E)
Space complexity: O(V+E)

C++

// Author: Huahua

// Author: Huahua, 791ms, 136 MB

class Solution {

public:

long long countPairs(int n, vector<vector<int>>& edges) {

vector<vector<int>> g(n);

for (const auto& e : edges) {

g[e[0]].push_back(e[1]);

g[e[1]].push_back(e[0]);

}

vector<int> seen(n);

long long cur = 0;

function<void(int)> dfs = [&](int u) {

++cur;

for (int v : g[u])

if (seen[v]++ == 0) dfs(v);

};

long long ans = 0;

for (int i = 0; i < n; ++i) {

if (seen[i]++) continue;

cur = 0;

dfs(i);

ans += (n - cur) * cur;

}

return ans / 2;

}

};

Solution 2: Union Find

Time complexity: O(V+E)
Space complexity: O(V)

C++

// Author: Huahua

class Solution {

public:

long long countPairs(int n, vector<vector<int>>& edges) {

vector<int> parents(n);

vector<int> counts(n, 1);

std::iota(begin(parents), end(parents), 0);

function<int(int)> find = [&](int x) {

if (parents[x] == x) return x;

return parents[x] = find(parents[x]);

};

for (const auto& e : edges) {

int ru = find(e[0]);

int rv = find(e[1]);

if (ru != rv) {

parents[rv] = ru;

counts[ru] += counts[rv];

}

long long ans = 0;

for (int i = 0; i < n; ++i)

ans += n - counts[find(i)];

return ans / 2;

}

};

花花酱 LeetCode 2192. All Ancestors of a Node in a Directed Acyclic Graph

By zxi on March 11, 2022

You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).

You are also given a 2D integer array edges, where edges[i] = [from_i, to_i] denotes that there is a unidirectional edge from from_i to to_i in the graph.

Return a list answer, where answer[i] is the list of ancestors of the i^th node, sorted in ascending order.

A node u is an ancestor of another node v if u can reach v via a set of edges.

Example 1:

Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.

Example 2:

Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.

Constraints:

1 <= n <= 1000
0 <= edges.length <= min(2000, n * (n - 1) / 2)
edges[i].length == 2
0 <= from_i, to_i <= n - 1
from_i != to_i
There are no duplicate edges.
The graph is directed and acyclic.

Solution: DFS

For each source node S, add it to all its reachable nodes by traversing the entire graph.
In one pass, only traverse each child node at most once.

Time complexity: O(VE)
Space complexity: (V+E)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {

vector<vector<int>> ans(n);

vector<vector<int>> g(n);

for (const auto& e : edges)

g[e[0]].push_back(e[1]);

function<void(int, int)> dfs = [&](int s, int u) -> void {

for (int v : g[u]) {

if (ans[v].empty() || ans[v].back() != s) {

ans[v].push_back(s);

dfs(s, v);

}

};

for (int i = 0; i < n; ++i)

dfs(i, i);

return ans;

}

};