SP Archives - Huahua's Tech Road

花花酱 Min Heap SP21

By zxi on November 18, 2020

C++

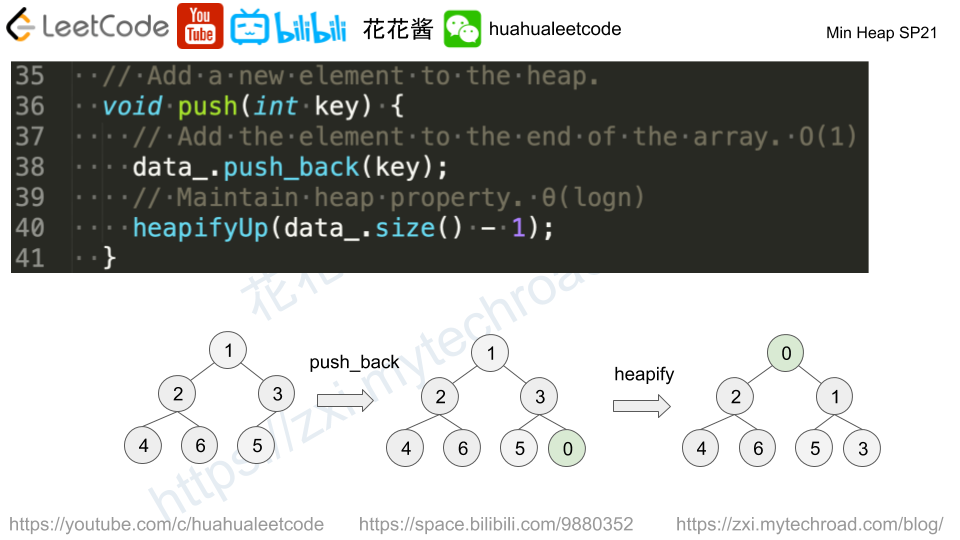
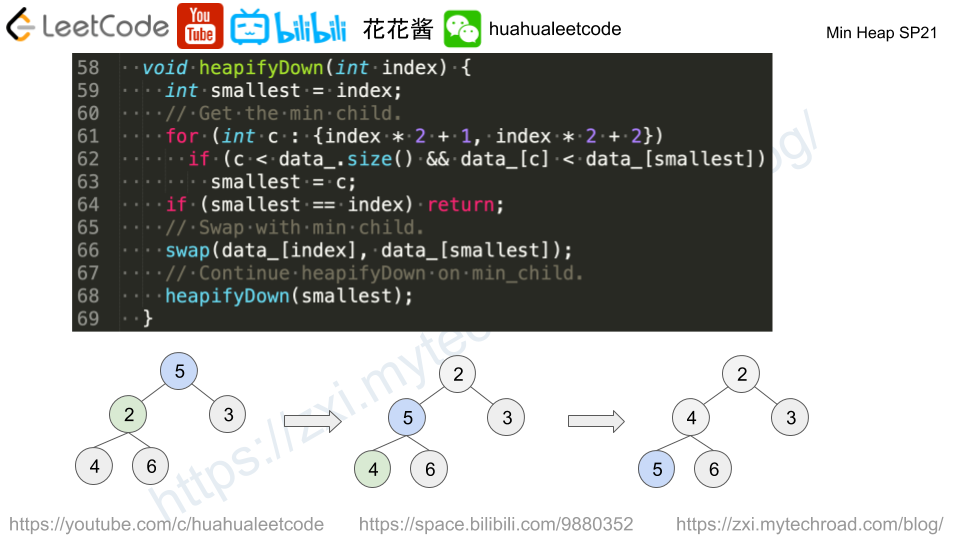
// Author: Huahua

#include <assert.h>

#include <iostream>

#include <vector>

using namespace std;

class MinHeap {

public:

// Return the min element.

int peek() const { return data_[0]; }

// Extract the min element.

int pop() {

// Swap the min element with the last one. O(1)

swap(data_.back(), data_[0]);

// Get the min element. O(1)

int min_el = data_.back();

// Evict the min element. O(1)

data_.pop_back();

// Maintain heap property. θ(logn)

heapifyDown(0);

return min_el;

}

// Add a new element to the heap.

void push(int key) {

// Add the element to the end of the array. O(1)

data_.push_back(key);

// Maintain heap property. θ(logn)

heapifyUp(data_.size() - 1);

}

// Return the size of the heap.

int size() const { return data_.size(); }

private:

void heapifyUp(int index) {

// Stop at root.

if (index == 0) return;

int parent = (index - 1) / 2;

// Stop if greater or euqal to parent.

if (data_[index] >= data_[parent]) return;

// Swap with parent.

swap(data_[index], data_[parent]);

// Continue heapifyUp on parent.

heapifyUp(parent);

}

void heapifyDown(int index) {

int left = index * 2 + 1;

int right = index * 2 + 2;

// Stop if has no left child.

if (left >= data_.size()) return;

// Get the min child.

int min_child =

right < data_.size() && data_[right] < data_[left] ? right : left;

// Stop if less or euqal to min child.

if (data_[index] <= data_[min_child])

return;

// Swap with min child.

swap(data_[index], data_[min_child]);

// Continue heapifyDown on min_child.

heapifyDown(min_child);

}

vector<int> data_;

};

int main() {

vector<int> data{5,1,3,5,3,4,3,7};

MinHeap heap;

for (int x : data)

heap.push(x);

vector<int> output;

while (heap.size())

output.push_back(heap.pop());

assert(output == vector<int>({1,3,3,3,4,5,5,7}));

}

Python3

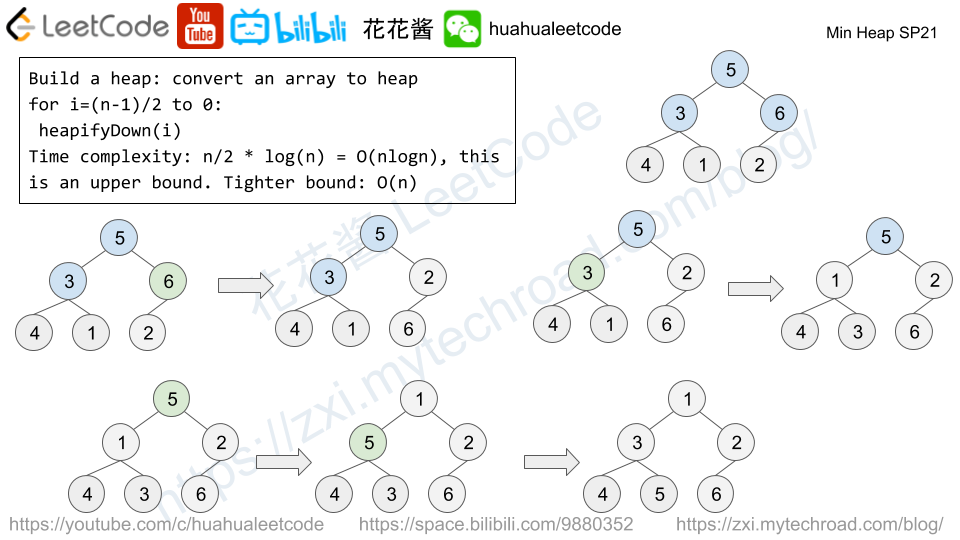
# Author: Huahua

class MinHeap:

def __init__(self, data = None):

self.data = list(data) if data else []

for i in range((len(self.data)) // 2, -1, -1):

self.heapifyDown(i)

def push(self, key):

self.data.append(key)

self.heapifyUp(len(self.data) - 1)

def pop(self):

self.swap(0, -1)

min_el = self.data.pop()

self.heapifyDown(0)

return min_el

def size(self):

return len(self.data)

def swap(self, i, j):

self.data[i], self.data[j] = self.data[j], self.data[i]

def heapifyDown(self, i):

smallest = i

for c in [2 * i + 1, 2 * i + 2]:

if c < self.size() and self.data[c] < self.data[smallest]: smallest = c

if smallest != i:

self.swap(i, smallest)

self.heapifyDown(smallest)

def heapifyUp(self, i):

if i == 0: return

parent = (i - 1) // 2

if self.data[i] >= self.data[parent]: return

self.swap(i, parent)

self.heapifyUp(parent)

def test():

data = [5,1,3,5,3,4,3,7]

heap = MinHeap()

for x in data: heap.push(x)

output = []

while heap.size():

output.append(heap.pop())

assert output == sorted(data)

def testBuildHeap():

data = [5,1,3,5,3,4,3,7]

heap = MinHeap(data)

output = []

while heap.size():

output.append(heap.pop())

assert output == sorted(data)

def main():

test()

testBuildHeap()

if __name__ == '__main__':

main()

Fast Power for DP SP20

By zxi on April 15, 2020

Iterative DP usually takes O(n) to compute dp[n] from dp[0], we could do better if the problem can be written as matrix multiplication. With fast power, dp[n] can be computed in O(logn)

KMP Algorithm SP19

By zxi on March 31, 2020

KMP Algorithm, KMP 字符串搜索算法

Time complexity: O(m+n)
Space complexity: O(m)

Implementation

C++

#include <iostream>

#include <vector>

using namespace std;

// Author: Huahua

namespace KMP {

vector<int> Build(const string& p) {

const int m = p.length();

vector<int> nxt{0, 0};

for (int i = 1, j = 0; i < m; ++i) {

while (j > 0 && p[i] != p[j])

j = nxt[j];

if (p[i] == p[j])

++j;

nxt.push_back(j);

}

return nxt;

}

vector<int> Match(const string& s, const string& p) {

vector<int> nxt(Build(p));

vector<int> ans;

const int n = s.length();

const int m = p.length();

for (int i = 0, j = 0; i < n; ++i) {

while (j > 0 && s[i] != p[j])

j = nxt[j];

if (s[i] == p[j])

++j;

if (j == m) {

ans.push_back(i - m + 1);

j = nxt[j];

}

return ans;

}

}; // namespace KMP

void CheckEQ(const vector<int>& actual, const vector<int>& expected) {

if (actual != expected) {

std::cout << "expected:";

for (int v : expected)

std::cout << " " << v;

std::cout << " actual:";

for (int v : actual)

std::cout << " " << v;

std::cout << std::endl;

} else {

std::cout << "PASS" << std::endl;

}

int main(int argc, char** argv) {

CheckEQ(KMP::Build("ABCDABD"), {0, 0, 0, 0, 0, 1, 2, 0});

CheckEQ(KMP::Build("AB"), {0, 0, 0});

CheckEQ(KMP::Build("A"), {0, 0});

CheckEQ(KMP::Build("AA"), {0, 0, 1});

CheckEQ(KMP::Build("AAA"), {0, 0, 1, 2});

CheckEQ(KMP::Build("AABA"), {0, 0, 1, 0, 1});

CheckEQ(KMP::Match("ABC ABCDAB ABCDABCDABDE", "ABCDABD"), {15});

CheckEQ(KMP::Match("ABC ABCDAB ABCDABCDABDE", "AB"), {0, 4, 8, 11, 15, 19});

CheckEQ(KMP::Match("ABC ABCDAB ABCDABCDABDE", "B"), {1, 5, 9, 12, 16, 20});

CheckEQ(KMP::Match("AAAAA", "A"), {0, 1, 2, 3, 4});

CheckEQ(KMP::Match("AAAAA", "AA"), {0, 1, 2, 3});

CheckEQ(KMP::Match("AAAAA", "AAA"), {0, 1, 2});

CheckEQ(KMP::Match("ABC", "ABC"), {0});

return 0;

}

Python3

#!/usr/bin/env python3

from typing import List

# Author: Huahua

def Build(p: str) -> List[int]:

m = len(p)

nxt = [0, 0]

j = 0

for i in range(1, m):

while j > 0 and p[i] != p[j]:

j = nxt[j]

if p[i] == p[j]:

j += 1

nxt.append(j)

return nxt

def Match(s: str, p: str) -> List[int]:

n, m = len(s), len(p)

nxt = Build(p)

ans = []

j = 0

for i in range(n):

while j > 0 and s[i] != p[j]:

j = nxt[j]

if s[i] == p[j]:

j += 1

if j == m:

ans.append(i - m + 1)

j = nxt[j]

return ans

def CheckEQ(actual, expected):

if actual != expected:

print('actual: %s, expected: %s' % (actual, expected))

else:

print('Pass')

if __name__ == "__main__":

CheckEQ(Build("ABCDABD"), [0, 0, 0, 0, 0, 1, 2, 0])

CheckEQ(Build("AB"), [0, 0, 0])

CheckEQ(Build("A"), [0, 0])

CheckEQ(Build("AA"), [0, 0, 1])

CheckEQ(Build("AAAA"), [0, 0, 1, 2, 3])

CheckEQ(Build("AABA"), [0, 0, 1, 0, 1])

CheckEQ(Match("ABC ABCDAB ABCDABCDABDE", "ABCDABD"), [15])

CheckEQ(Match("ABC ABCDAB ABCDABCDABDE", "AB"), [0, 4, 8, 11, 15, 19])

CheckEQ(Match("ABC ABCDAB ABCDABCDABDE", "B"), [1, 5, 9, 12, 16, 20])

CheckEQ(Match("AAAAA", "A"), [0, 1, 2, 3, 4])

CheckEQ(Match("AAAAA", "AA"), [0, 1, 2, 3])

CheckEQ(Match("AAAAA", "AAAA"), [0, 1])

CheckEQ(Match("AAAAA", "AAAAA"), [0])

CheckEQ(Match("AABAABA", "AABA"), [0, 3])

Applications

LeetCode 28. strStr()

C++

// Author: Huahua

class Solution {

public:

int strStr(string haystack, string needle) {

if (needle.empty()) return 0;

auto matches = KMP::Match(haystack, needle);

return matches.empty() ? -1 : matches[0];

}

};

LeetCode 459. Repeated Substring Pattern

C++

// Author: Huahua

class Solution {

public:

bool repeatedSubstringPattern(string str) {

const int n = str.length();

auto nxt = KMP::Build(str);

return nxt[n] && nxt[n] % (n - nxt[n]) == 0;

}

};

1392. Longest Happy Prefix

C++

// Author: Huahua

class Solution {

public:

string longestPrefix(const string& s) {

return s.substr(0, KMP::Build(s).back());

}

};

花花酱 Minimum Spanning Tree (MST) 最小生成树 SP18

By zxi on January 24, 2020

Prim’s Algorithm

Time complexity: O(ElogV)
Space complexity: O(V+E)

C++

// Author: Huahua

#include <iostream>

#include <queue>

#include <vector>

using namespace std;

int main(int argc, char** argv) {

const int n = 4;

vector<vector<int>> edges{{0,1,1},{0,3,3},{0,2,6},{2,3,2},{1,2,4},{1,3,5}};

vector<vector<pair<int, int>>> g(n);

for (const auto& e : edges) {

g[e[0]].emplace_back(e[1], e[2]);

g[e[1]].emplace_back(e[0], e[2]);

}

priority_queue<pair<int, int>> q; // (-w, v)

vector<int> seen(n);

q.emplace(0, 0); // (-w, v)

int cost = 0;

for (int i = 0; i < n; ++i) {

while (true) {

const int w = -q.top().first;

const int v = q.top().second;

q.pop();

if (seen[v]++) continue;

cost += w;

for (const auto& p : g[v]) {

if (seen[p.first]) continue;

q.emplace(-p.second, p.first);

}

break;

}

cout << cost << endl;

return 0;

}

Python

# Author: Huahua

from collections import defaultdict

from heapq import *

n = 4

edges = [[0,1,1],[0,3,3],[0,2,6],[2,3,2],[1,2,4],[1,3,5]]

g = defaultdict(list)

for e in edges:

g[e[0]].append((e[1], e[2]))

g[e[1]].append((e[0], e[2]))

q = []

cost = 0

seen = set()

heappush(q, (0, 0))

for _ in range(n):

while True:

w, u = heappop(q)

if u in seen: continue

cost += w

seen.add(u)

for v, w in g[u]:

if v in seen: continue

heappush(q, (w, v))

break

print(cost)

Kruskal’s Algorithm

Time complexity: O(ElogV)
Space complexity: O(V+E)

C++

// Author: Huahua

#include <iostream>

#include <queue>

#include <vector>

#include <functional>

#include <numeric>

using namespace std;

int main(int argc, char** argv) {

const int n = 4;

vector<vector<int>> edges{{0,1,1},{0,3,3},{0,2,6},{2,3,2},{1,2,4},{1,3,5}};

vector<vector<int>> q; // (w, u, v)

for (const auto& e : edges)

q.push_back({e[2], e[0], e[1]});

sort(begin(q), end(q));

vector<int> p(n);

iota(begin(p), end(p), 0);

function<int(int)> find = [&](int x) {

return x == p[x] ? x : p[x] = find(p[p[x]]);

};

int cost = 0;

for (const auto& t : q) {

int w = t[0], u = t[1], v = t[2];

int ru = find(u), rv = find(v);

if (ru == rv) continue;

p[ru] = rv; // merge (u, v)

cost += w;

}

cout << cost << endl;

return 0;

}

Python

from collections import defaultdict

from heapq import *

n = 4

edges = [[0,1,1],[0,3,3],[0,2,6],[2,3,2],[1,2,4],[1,3,5]]

p = list(range(n))

def find(x):

if x != p[x]: p[x] = find(p[p[x]])

return p[x]

cost = 0

for u, v, w in sorted(edges, key=lambda x: x[2]):

ru, rv = find(u), find(v)

if ru == rv: continue

p[ru] = rv

cost += w

print(cost)

花花酱 Binary Search II SP17

By zxi on April 20, 2019

Binary Search I SP5

For the given function g(x) and a range [l, r] find the smallest int number m such that g(m) is True, if not found, return r + 1.

Posts published in “SP”

花花酱 Min Heap SP21

C++

Python3

Fast Power for DP SP20

KMP Algorithm SP19

Implementation

C++

Python3

Applications

C++

C++

C++

花花酱 Minimum Spanning Tree (MST) 最小生成树 SP18

Prim’s Algorithm

C++

Python

Kruskal’s Algorithm

C++

Python

花花酱 Binary Search II SP17