Posts tagged as “matrix”

花花酱 LeetCode 2661. First Completely Painted Row or Column

By zxi on April 30, 2023

You are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].

Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].

Return the smallest index i at which either a row or a column will be completely painted in mat.

Example 1:

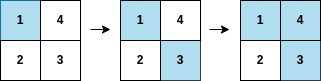
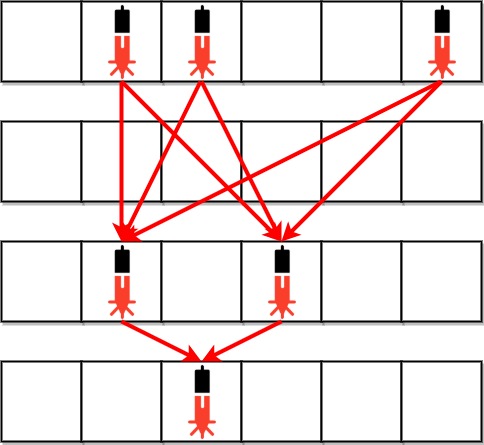
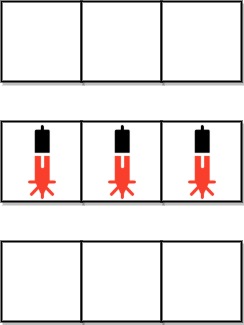
Input: arr = [1,3,4,2], mat = [[1,4],[2,3]]
Output: 2
Explanation: The moves are shown in order, and both the first row and second column of the matrix become fully painted at arr[2].

Example 2:

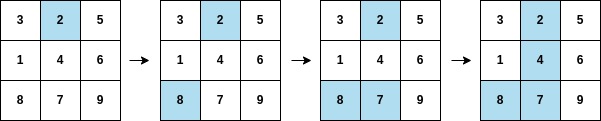
Input: arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
Output: 3
Explanation: The second column becomes fully painted at arr[3].

Constraints:

m == mat.length
n = mat[i].length
arr.length == m * n
1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
1 <= arr[i], mat[r][c] <= m * n
All the integers of arr are unique.
All the integers of mat are unique.

Solution: Map + Counter

Use a map to store the position of each integer.

Use row counters and column counters to track how many elements have been painted.

Time complexity: O(m*n + m + n)
Space complexity: O(m*n + m + n)

C++

// Author: Huahua

class Solution {

public:

int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {

const int m = mat.size();

const int n = mat[0].size();

vector<int> rows(m);

vector<int> cols(n);

vector<pair<int, int>> pos(m * n + 1);

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

pos[mat[i][j]] = {i, j};

for (int i = 0; i < arr.size(); ++i) {

auto [r, c] = pos[arr[i]];

if (++rows[r] == n) return i;

if (++cols[c] == m) return i;

}

return -1;

}

};

花花酱 LeetCode 2639. Find the Width of Columns of a Grid

By zxi on April 29, 2023

You are given a 0-indexed m x n integer matrix grid. The width of a column is the maximum length of its integers.

For example, if grid = [[-10], [3], [12]], the width of the only column is 3 since -10 is of length 3.

Return an integer array ans of size n where ans[i] is the width of the i^th column.

The length of an integer x with len digits is equal to len if x is non-negative, and len + 1 otherwise.

Example 1:

Input: grid = [[1],[22],[333]]
Output: [3]
Explanation: In the 0^th column, 333 is of length 3.

Example 2:

Input: grid = [[-15,1,3],[15,7,12],[5,6,-2]]
Output: [3,1,2]
Explanation: 
In the 0^th column, only -15 is of length 3.
In the 1^st column, all integers are of length 1. 
In the 2^nd column, both 12 and -2 are of length 2.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
-10⁹ <= grid[r][c] <= 10⁹

Solution: Simulation

Note: width of ‘0’ is 1.

Time complexity: O(m*n*log(x))
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<int> findColumnWidth(vector<vector<int>>& grid) {

vector<int> ans;

for (int j = 0; j < grid[0].size(); ++j) {

int maxWidth = 1;

for (int i = 0; i < grid.size(); ++i) {

int x = grid[i][j];

int width = 0;

if (x < 0) {

x = -x;

++width;

}

while (x) {

x /= 10;

++width;

}

maxWidth = max(maxWidth, width);

}

ans.push_back(maxWidth);

}

return ans;

}

};

花花酱 LeetCode 2643. Row With Maximum Ones

By zxi on April 28, 2023

Given a m x n binary matrix mat, find the 0-indexed position of the row that contains the maximum count of ones, and the number of ones in that row.

In case there are multiple rows that have the maximum count of ones, the row with the smallest row number should be selected.

Return an array containing the index of the row, and the number of ones in it.

Example 1:

Input: mat = [[0,1],[1,0]]
Output: [0,1]
Explanation: Both rows have the same number of 1's. So we return the index of the smaller row, 0, and the maximum count of ones (1). So, the answer is [0,1].

Example 2:

Input: mat = [[0,0,0],[0,1,1]]
Output: [1,2]
Explanation: The row indexed 1 has the maximum count of ones (2). So we return its index, 1, and the count. So, the answer is [1,2].

Example 3:

Input: mat = [[0,0],[1,1],[0,0]]
Output: [1,2]
Explanation: The row indexed 1 has the maximum count of ones (2). So the answer is [1,2].

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 100
mat[i][j] is either 0 or 1.

Solution: Counting

Time complexity: O(m*n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<int> rowAndMaximumOnes(vector<vector<int>>& mat) {

vector<int> ans(2);

for (int i = 0; i < mat.size(); ++i) {

int ones = accumulate(begin(mat[i]), end(mat[i]), 0);

if (ones > ans[1]) {

ans[0] = i;

ans[1] = ones;

}

return ans;

}

};

花花酱 LeetCode 2373. Largest Local Values in a Matrix

By zxi on August 14, 2022

You are given an n x n integer matrix grid.

Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:

maxLocal[i][j] is equal to the largest value of the 3 x 3 matrix in grid centered around row i + 1 and column j + 1.

In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.

Return the generated matrix.

Example 1:

Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]
Output: [[9,9],[8,6]]
Explanation: The diagram above shows the original matrix and the generated matrix.
Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.

Example 2:

Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]
Output: [[2,2,2],[2,2,2],[2,2,2]]
Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.

Constraints:

n == grid.length == grid[i].length
3 <= n <= 100
1 <= grid[i][j] <= 100

Solution: Brute Force

Time complexity: O(n*n*9)
Space complexity: O(n*n)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> largestLocal(vector<vector<int>>& grid) {

const int m = grid.size() - 2;

vector<vector<int>> ans(m, vector<int>(m));

for (int i = 0; i < m; ++i)

for (int j = 0; j < m; ++j)

for (int dy = 0; dy <= 2; ++dy)

for (int dx = 0; dx <= 2; ++dx)

ans[i][j] = max(ans[i][j], grid[i + dy][j + dx]);

return ans;

}

};

花花酱 LeetCode 2125. Number of Laser Beams in a Bank

By zxi on January 2, 2022

Anti-theft security devices are activated inside a bank. You are given a 0-indexed binary string array bank representing the floor plan of the bank, which is an m x n 2D matrix. bank[i] represents the i^th row, consisting of '0's and '1's. '0' means the cell is empty, while'1' means the cell has a security device.

There is one laser beam between any two security devices if both conditions are met:

The two devices are located on two different rows: r₁ and r₂, where r₁ < r₂.
For each row i where r₁ < i < r₂, there are no security devices in the i^th row.

Laser beams are independent, i.e., one beam does not interfere nor join with another.

Return the total number of laser beams in the bank.

Example 1:

Input: bank = ["011001","000000","010100","001000"]
Output: 8
Explanation: Between each of the following device pairs, there is one beam. In total, there are 8 beams:
 * bank[0][1] -- bank[2][1]
 * bank[0][1] -- bank[2][3]
 * bank[0][2] -- bank[2][1]
 * bank[0][2] -- bank[2][3]
 * bank[0][5] -- bank[2][1]
 * bank[0][5] -- bank[2][3]
 * bank[2][1] -- bank[3][2]
 * bank[2][3] -- bank[3][2]
Note that there is no beam between any device on the 0^th row with any on the 3^rd row.
This is because the 2^nd row contains security devices, which breaks the second condition.

Example 2:

Input: bank = ["000","111","000"]
Output: 0
Explanation: There does not exist two devices located on two different rows.

Constraints:

m == bank.length
n == bank[i].length
1 <= m, n <= 500
bank[i][j] is either '0' or '1'.

Solution: Rule of product

Just need to remember the # of devices of prev non-empty row.
# of beams between two non-empty row equals to row[i] * row[j]
ans += prev * curr

Time complexity: O(m*n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int numberOfBeams(vector<string>& bank) {

int ans = 0;

int prev = 0;

for (const string& row : bank)

if (int curr = count(begin(row), end(row), '1')) {

ans += prev * curr;

prev = curr;

}

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def numberOfBeams(self, bank: List[str]) -> int:

ans = prev = 0

for row in bank:

if curr := row.count('1'):

ans += prev * curr

prev = curr

return ans