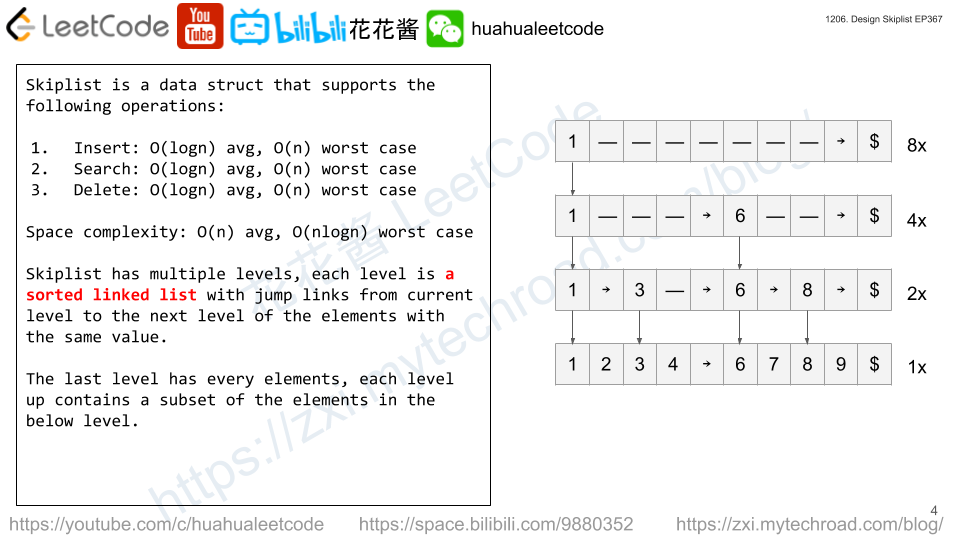
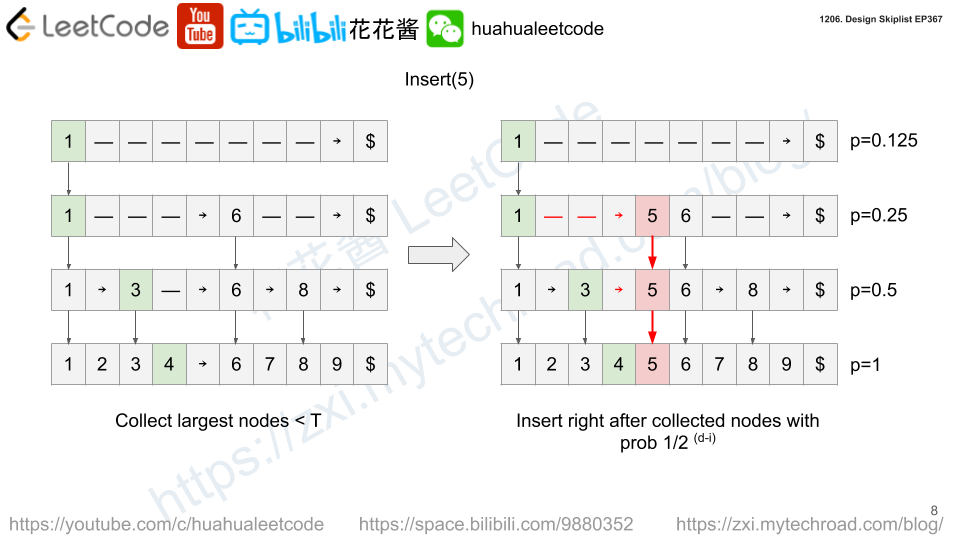
There is an ATM machine that stores banknotes of 5 denominations: 20, 50, 100, 200, and 500 dollars. Initially the ATM is empty. The user can use the machine to deposit or withdraw any amount of money.
When withdrawing, the machine prioritizes using banknotes of larger values.
- For example, if you want to withdraw
$300and there are2$50banknotes,1$100banknote, and1$200banknote, then the machine will use the$100and$200banknotes. - However, if you try to withdraw
$600and there are3$200banknotes and1$500banknote, then the withdraw request will be rejected because the machine will first try to use the$500banknote and then be unable to use banknotes to complete the remaining$100. Note that the machine is not allowed to use the$200banknotes instead of the$500banknote.
Implement the ATM class:
ATM()Initializes the ATM object.void deposit(int[] banknotesCount)Deposits new banknotes in the order$20,$50,$100,$200, and$500.int[] withdraw(int amount)Returns an array of length5of the number of banknotes that will be handed to the user in the order$20,$50,$100,$200, and$500, and update the number of banknotes in the ATM after withdrawing. Returns[-1]if it is not possible (do not withdraw any banknotes in this case).
Example 1:
Input
["ATM", "deposit", "withdraw", "deposit", "withdraw", "withdraw"]
[[], [[0,0,1,2,1]], [600], [[0,1,0,1,1]], [600], [550]]
Output
[null, null, [0,0,1,0,1], null, [-1], [0,1,0,0,1]]
Explanation
ATM atm = new ATM();
atm.deposit([0,0,1,2,1]); // Deposits 1 $100 banknote, 2 $200 banknotes,
// and 1 $500 banknote.
atm.withdraw(600); // Returns [0,0,1,0,1]. The machine uses 1 $100 banknote
// and 1 $500 banknote. The banknotes left over in the
// machine are [0,0,0,2,0].
atm.deposit([0,1,0,1,1]); // Deposits 1 $50, $200, and $500 banknote.
// The banknotes in the machine are now [0,1,0,3,1].
atm.withdraw(600); // Returns [-1]. The machine will try to use a $500 banknote
// and then be unable to complete the remaining $100,
// so the withdraw request will be rejected.
// Since the request is rejected, the number of banknotes
// in the machine is not modified.
atm.withdraw(550); // Returns [0,1,0,0,1]. The machine uses 1 $50 banknote
// and 1 $500 banknote.
Constraints:
banknotesCount.length == 50 <= banknotesCount[i] <= 1091 <= amount <= 109- At most
5000calls in total will be made towithdrawanddeposit. - At least one call will be made to each function
withdrawanddeposit.
Solution:
Follow the rules. Note: total count can be very large, use long instead.
Time complexity: O(1)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
// Author: Huahua constexpr int kNotes = 5; constexpr long notes[kNotes] = {20, 50, 100, 200, 500}; class ATM { public: ATM(): counts(kNotes) {} void deposit(vector<int> banknotesCount) { for (int i = 0; i < kNotes; ++i) counts[i] += banknotesCount[i]; } vector<int> withdraw(int amount) { vector<int> ans(kNotes); vector<long> tmp(counts); for (int i = kNotes - 1; i >= 0; --i) if (amount >= notes[i]) { int c = min(counts[i], amount / notes[i]); ans[i] = c; amount -= c * notes[i]; tmp[i] -= c; } if (amount != 0) return {-1}; counts.swap(tmp); return ans; } private: vector<long> counts; }; |