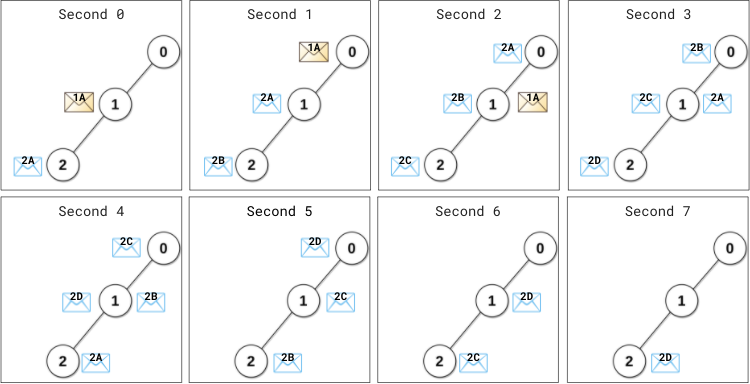
You are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:
0 represents a wall that you cannot pass through.
1 represents an empty cell that you can freely move to and from.
All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.
It takes 1 step to travel between adjacent grid cells.
You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position (row, col) and are interested only in items with a price in the range of [low, high] (inclusive). You are further given an integer k.
You are interested in the positions of the khighest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:
Distance, defined as the length of the shortest path from the start (shorter distance has a higher rank).
Price (lower price has a higher rank, but it must be in the price range).
The row number (smaller row number has a higher rank).
The column number (smaller column number has a higher rank).
Return the k highest-ranked items within the price range sorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.
Example 1:
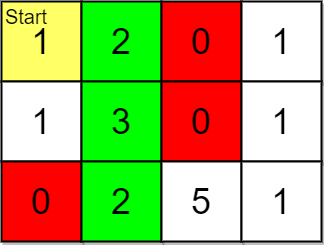
Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
Output: [[0,1],[1,1],[2,1]]
Explanation: You start at (0,0).
With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2).
The ranks of these items are:
- (0,1) with distance 1
- (1,1) with distance 2
- (2,1) with distance 3
- (2,2) with distance 4
Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).
Example 2:
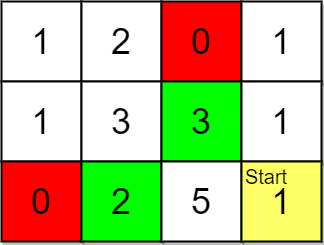
Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
Output: [[2,1],[1,2]]
Explanation: You start at (2,3).
With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1).
The ranks of these items are:
- (2,1) with distance 2, price 2
- (1,2) with distance 2, price 3
- (1,1) with distance 3
- (0,1) with distance 4
Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).
Example 3:
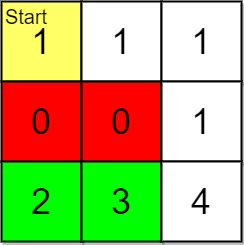
Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
Output: [[2,1],[2,0]]
Explanation: You start at (0,0).
With a price range of [2,3], we can take items from (2,0) and (2,1).
The ranks of these items are:
- (2,1) with distance 5
- (2,0) with distance 6
Thus, the 2 highest ranked items in the price range are (2,1) and (2,0).
Note that k = 3 but there are only 2 reachable items within the price range.
Constraints:
m == grid.length
n == grid[i].length
1 <= m, n <= 105
1 <= m * n <= 105
0 <= grid[i][j] <= 105
pricing.length == 2
2 <= low <= high <= 105
start.length == 2
0 <= row <= m - 1
0 <= col <= n - 1
grid[row][col] > 0
1 <= k <= m * n
Solution: BFS + Sorting
Use BFS to collect reachable cells and sort afterwards.
Time complexity: O(mn + KlogK) where K = # of reachable cells.
You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.
In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrancedoes not count as an exit.
Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.
Example 1:
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2]
Output: 1
Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3].
Initially, you are at the entrance cell [1,2].
- You can reach [1,0] by moving 2 steps left.
- You can reach [0,2] by moving 1 step up.
It is impossible to reach [2,3] from the entrance.
Thus, the nearest exit is [0,2], which is 1 step away.
Example 2:
Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0]
Output: 2
Explanation: There is 1 exit in this maze at [1,2].
[1,0] does not count as an exit since it is the entrance cell.
Initially, you are at the entrance cell [1,0].
- You can reach [1,2] by moving 2 steps right.
Thus, the nearest exit is [1,2], which is 2 steps away.
Example 3:
Input: maze = [[".","+"]], entrance = [0,0]
Output: -1
Explanation: There are no exits in this maze.
Constraints:
maze.length == m
maze[i].length == n
1 <= m, n <= 100
maze[i][j] is either '.' or '+'.
entrance.length == 2
0 <= entrancerow < m
0 <= entrancecol < n
entrance will always be an empty cell.
Solution: BFS
Use BFS to find the shortest path. We can re-use the board for visited array.
You are given a list of bombs. The range of a bomb is defined as the area where its effect can be felt. This area is in the shape of a circle with the center as the location of the bomb.
The bombs are represented by a 0-indexed 2D integer array bombs where bombs[i] = [xi, yi, ri]. xi and yi denote the X-coordinate and Y-coordinate of the location of the ith bomb, whereas ri denotes the radius of its range.
You may choose to detonate a single bomb. When a bomb is detonated, it will detonate all bombs that lie in its range. These bombs will further detonate the bombs that lie in their ranges.
Given the list of bombs, return the maximum number of bombs that can be detonated if you are allowed to detonate only one bomb.
Example 1:
Input: bombs = [[2,1,3],[6,1,4]]
Output: 2
Explanation:
The above figure shows the positions and ranges of the 2 bombs.
If we detonate the left bomb, the right bomb will not be affected.
But if we detonate the right bomb, both bombs will be detonated.
So the maximum bombs that can be detonated is max(1, 2) = 2.
Example 2:
Input: bombs = [[1,1,5],[10,10,5]]
Output: 1
Explanation:
Detonating either bomb will not detonate the other bomb, so the maximum number of bombs that can be detonated is 1.
Example 3:
Input: bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
Output: 5
Explanation:
The best bomb to detonate is bomb 0 because:
- Bomb 0 detonates bombs 1 and 2. The red circle denotes the range of bomb 0.
- Bomb 2 detonates bomb 3. The blue circle denotes the range of bomb 2.
- Bomb 3 detonates bomb 4. The green circle denotes the range of bomb 3.
Thus all 5 bombs are detonated.
Constraints:
1 <= bombs.length <= 100
bombs[i].length == 3
1 <= xi, yi, ri <= 105
Solution: Simulation w/ BFS
Enumerate the bomb to detonate, and simulate the process using BFS.
You are given a 0-indexed integer array nums containing distinct numbers, an integer start, and an integer goal. There is an integer x that is initially set to start, and you want to perform operations on x such that it is converted to goal. You can perform the following operation repeatedly on the number x:
If 0 <= x <= 1000, then for any index i in the array (0 <= i < nums.length), you can set x to any of the following:
x + nums[i]
x - nums[i]
x ^ nums[i] (bitwise-XOR)
Note that you can use each nums[i] any number of times in any order. Operations that set x to be out of the range 0 <= x <= 1000 are valid, but no more operations can be done afterward.
Return the minimum number of operations needed to convert x = start into goal, and -1 if it is not possible.
Example 1:
Input: nums = [1,3], start = 6, goal = 4
Output: 2
Explanation:
We can go from 6 → 7 → 4 with the following 2 operations.
- 6 ^ 1 = 7
- 7 ^ 3 = 4
Example 2:
Input: nums = [2,4,12], start = 2, goal = 12
Output: 2
Explanation:
We can go from 2 → 14 → 12 with the following 2 operations.
- 2 + 12 = 14
- 14 - 2 = 12
Example 3:
Input: nums = [3,5,7], start = 0, goal = -4
Output: 2
Explanation:
We can go from 0 → 3 → -4 with the following 2 operations.
- 0 + 3 = 3
- 3 - 7 = -4
Note that the last operation sets x out of the range 0 <= x <= 1000, which is valid.
Example 4:
Input: nums = [2,8,16], start = 0, goal = 1
Output: -1
Explanation:
There is no way to convert 0 into 1.
Example 5:
1
2
3
4
5
6
7
<strong>Input:</strong>nums=[1],start=0,goal=3
<strong>Output:</strong>3
<strong>Explanation:</strong>
We can go from0→1→2→3with the following3operations.
