Posts published in “Medium”

花花酱 LeetCode 769. Max Chunks To Make Sorted

By zxi on February 2, 2018

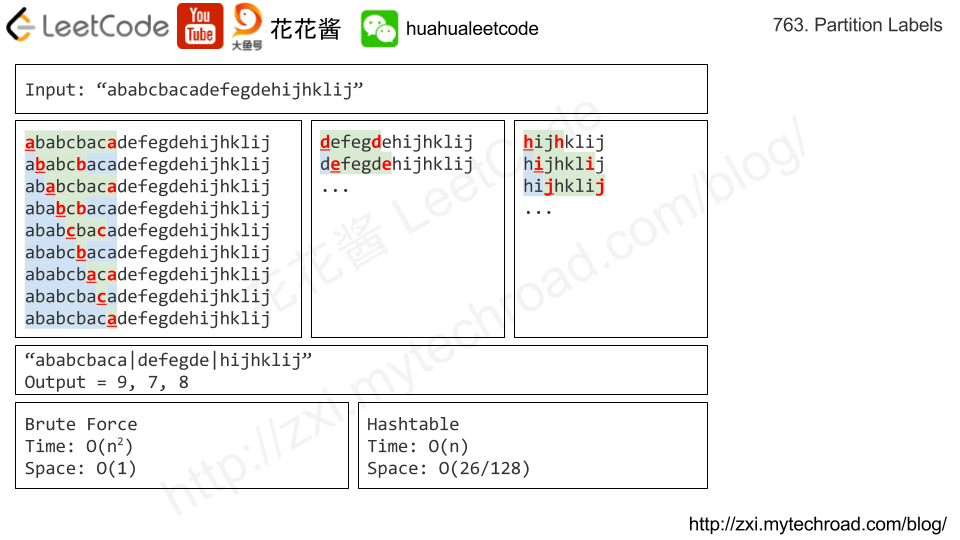
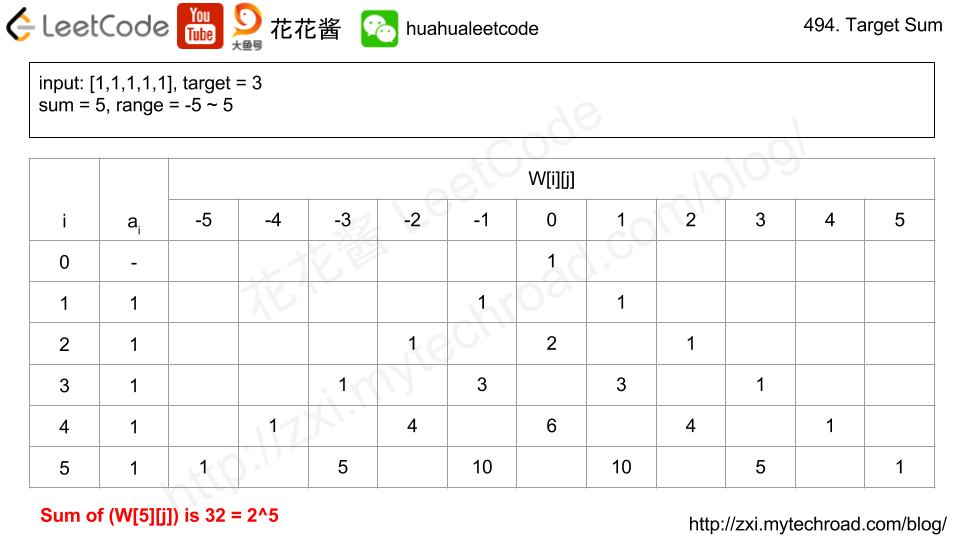
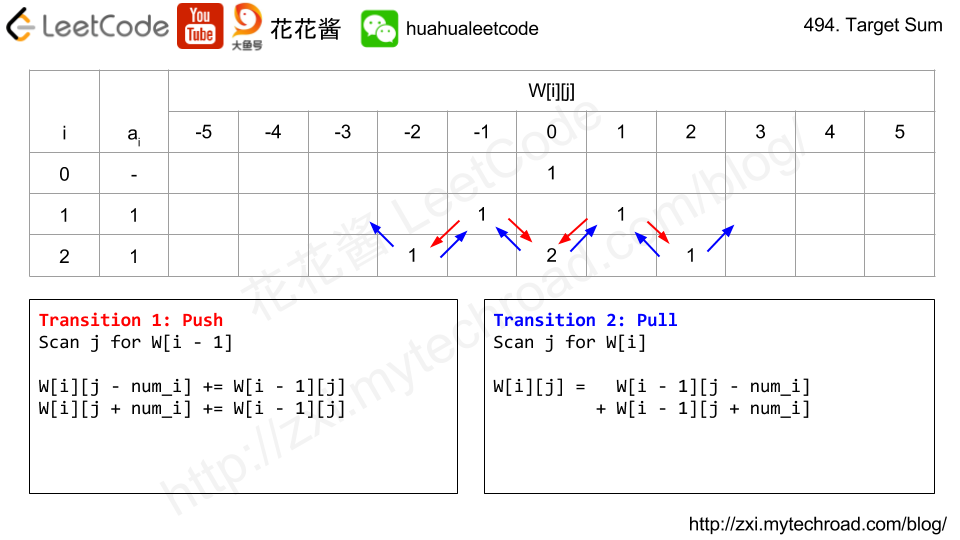
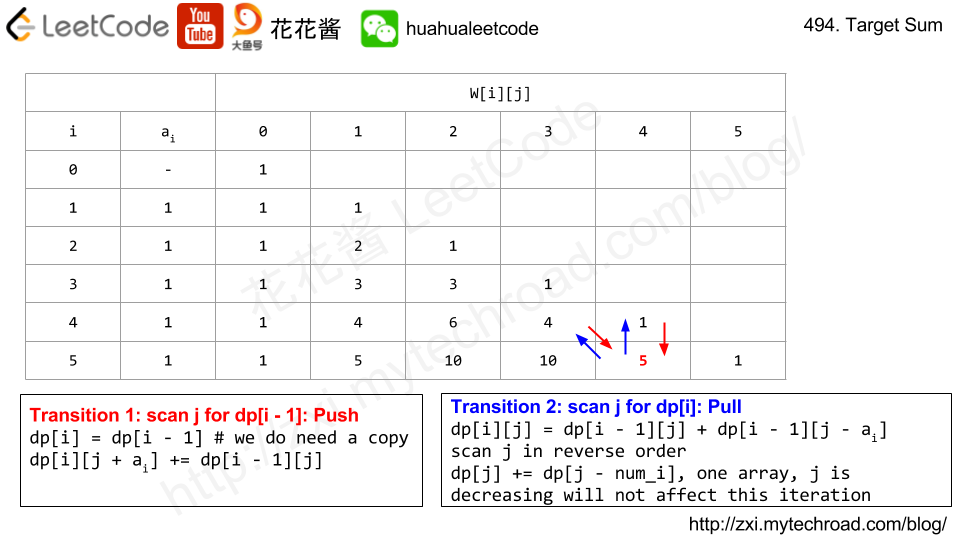
题目大意：给你一个0 ~ n-1的排列，问你最多能分成几组，每组分别排序后能够组成0 ~ n-1。

Given an array arr that is a permutation of [0, 1, ..., arr.length - 1], we split the array into some number of “chunks” (partitions), and individually sort each chunk. After concatenating them, the result equals the sorted array.

What is the most number of chunks we could have made?

Example 1:

Input: arr = [4,3,2,1,0]

Output: 1

Explanation:

Splitting into two or more chunks will not return the required result.

For example, splitting into [4, 3], [2, 1, 0] will result in [3, 4, 0, 1, 2], which isn't sorted.

Example 2:

Input: arr = [1,0,2,3,4]

Output: 4

Explanation:

We can split into two chunks, such as [1, 0], [2, 3, 4].

However, splitting into [1, 0], [2], [3], [4] is the highest number of chunks possible.

Note:

arr will have length in range [1, 10].
arr[i] will be a permutation of [0, 1, ..., arr.length - 1].

Solution 1: Max so far / Set

Time complexity: O(nlogn)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 3 ms

class Solution {

public:

int maxChunksToSorted(vector<int>& arr) {

int ans = 0;

set<int> s;

for (int i = 0; i < arr.size(); ++i) {

s.insert(arr[i]);

if (*s.rbegin() == i) ++ans;

}

return ans;

}

};

Solution 2: Max so far

Time complexity: O(n)

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int maxChunksToSorted(vector<int>& arr) {

int ans = 0;

int m = 0;

for (int i = 0; i < arr.size(); ++i) {

m = max(m, arr[i]);

if (m == i) ++ans;

}

return ans;

}

};

Java

// Author: Huahua

// Running time: 5 ms

class Solution {

public int maxChunksToSorted(int[] arr) {

int max = 0;

int ans = 0;

for (int i = 0; i < arr.length; ++i) {

max = Math.max(max, arr[i]);

if (max == i) ++ans;

}

return ans;

}

Python3

"""

Author: Huahua

Running time: 53 ms

"""

class Solution:

def maxChunksToSorted(self, arr):

m = 0

ans = 0

for i, n in enumerate(arr):

if n > m: m = n

if m == i: ans += 1

return ans

花花酱 LeetCode 763. Partition Labels

By zxi on January 25, 2018

题目大意：把字符串分割成尽量多的不重叠子串，输出子串的长度数组。要求相同字符只能出现在一个子串中。

Problem:

A string S of lowercase letters is given. We want to partition this string into as many parts as possible so that each letter appears in at most one part, and return a list of integers representing the size of these parts.

Example 1:

Input: S = "ababcbacadefegdehijhklij"

Output: [9,7,8]

Explanation:

The partition is "ababcbaca", "defegde", "hijhklij".

This is a partition so that each letter appears in at most one part.

A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less parts.

Solution 0: Brute Force

Time complexity: O(n^2)

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 15 ms

class Solution {

public:

vector<int> partitionLabels(string S) {

vector<int> ans;

size_t start = 0;

size_t end = 0;

for (size_t i = 0; i < S.size(); ++i) {

end = max(end, S.find_last_of(S[i]));

if (i == end) {

ans.push_back(end - start + 1);

start = end + 1;

}

return ans;

}

};

Python

"""

Author: Huahua

Running time : 48 ms

"""

class Solution:

def partitionLabels(self, S):

ans = []

start, end = 0, 0

for i in range(len(S)):

end = max(end, S.rfind(S[i]))

if i == end:

ans.append(end - start + 1)

start = end + 1

return ans

Solution 1: Greedy

Time complexity: O(n)

Space complexity: O(26/128)

C++

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

vector<int> partitionLabels(string S) {

vector<int> last_index(128, 0);

for (int i = 0; i < S.size(); ++i)

last_index[S[i]] = i;

vector<int> ans;

int start = 0;

int end = 0;

for (int i = 0; i < S.size(); ++i) {

end = max(end, last_index[S[i]]);

if (i == end) {

ans.push_back(end - start + 1);

start = end + 1;

}

return ans;

}

};

Java

// Author: Huahua

// Running time: 16 ms

class Solution {

public List<Integer> partitionLabels(String S) {

int lastIndex[] = new int[128];

for (int i = 0; i < S.length(); ++i)

lastIndex[(int)S.charAt(i)] = i;

List<Integer> ans = new ArrayList<>();

int start = 0;

int end = 0;

for (int i = 0; i < S.length(); ++i) {

end = Math.max(end, lastIndex[(int)S.charAt(i)]);

if (i == end) {

ans.add(end - start + 1);

start = end + 1;

}

return ans;

}

Python3

"""

Author: Huahua

Running time: 78 ms

"""

class Solution:

def partitionLabels(self, S):

last_index = {}

for i, ch in enumerate(S):

last_index[ch] = i

start = end = 0

ans = []

for i, ch in enumerate(S):

end = max(end, last_index[ch])

if i == end:

ans.append(end - start + 1)

start = end + 1

return ans

花花酱 LeetCode 494. Target Sum

By zxi on January 9, 2018

题目大意：给你一串数字，你可以在每个数字前放置+或-，问有多少种方法可以使得表达式的值等于target。You are given a list of non-negative integers, a1, a2, …, an, and a target, S. Now you have 2 symbols + and -. For each integer, you should choose one from + and - as its new symbol.

Find out how many ways to assign symbols to make sum of integers equal to target S.

Example 1:

Input: nums is [1, 1, 1, 1, 1], S is 3.

Output: 5

Explanation:

-1+1+1+1+1 = 3

+1-1+1+1+1 = 3

+1+1-1+1+1 = 3

+1+1+1-1+1 = 3

+1+1+1+1-1 = 3

There are 5 ways to assign symbols to make the sum of nums be target 3.

Note:

The length of the given array is positive and will not exceed 20.
The sum of elements in the given array will not exceed 1000.
Your output answer is guaranteed to be fitted in a 32-bit integer.

Idea: DP

Solution 1: DP

Time complexity: O(n*sum)

Space complexity: O(n*sum)

C++

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

int findTargetSumWays(vector<int>& nums, int S) {

const int n = nums.size();

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum < S) return 0;

const int offset = sum;

// ways[i][j] means total ways to sum up to (j - offset) using nums[0] ~ nums[i - 1].

vector<vector<int>> ways(n + 1, vector<int>(sum + offset + 1, 0));

ways[0][offset] = 1;

for (int i = 0; i < n; ++i) {

for (int j = nums[i]; j < 2 * sum + 1 - nums[i]; ++j)

if (ways[i][j]) {

ways[i + 1][j + nums[i]] += ways[i][j];

ways[i + 1][j - nums[i]] += ways[i][j];

}

return ways.back()[S + offset];

}

};

C++ SC O(n)

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

int findTargetSumWays(vector<int>& nums, int S) {

const int n = nums.size();

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum < std::abs(S)) return 0;

const int kOffset = sum;

const int kMaxN = sum * 2 + 1;

vector<int> ways(kMaxN, 0);

ways[kOffset] = 1;

for (int num : nums) {

vector<int> tmp(kMaxN, 0);

for (int i = num; i < kMaxN - num; ++i)

if (ways[i]) {

tmp[i + num] += ways[i];

tmp[i - num] += ways[i];

}

std::swap(ways, tmp);

}

return ways[S + kOffset];

}

};

Java

// Author: Huahua

// Running time: 28 ms

class Solution {

public int findTargetSumWays(int[] nums, int S) {

int sum = 0;

for (final int num : nums)

sum += num;

if (sum < S) return 0;

final int kOffset = sum;

final int kMaxN = sum * 2 + 1;

int[] ways = new int[kMaxN];

ways[kOffset] = 1;

for (final int num : nums) {

int[] tmp = new int[kMaxN];

for (int i = num; i < kMaxN - num; ++i) {

tmp[i + num] += ways[i];

tmp[i - num] += ways[i];

}

ways = tmp;

}

return ways[S + kOffset];

}

C++ / V2

// Author: Huahua

// Running time: 17 ms

class Solution {

public:

int findTargetSumWays(vector<int>& nums, int S) {

const int n = nums.size();

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum < std::abs(S)) return 0;

const int kOffset = sum;

const int kMaxN = sum * 2 + 1;

vector<int> ways(kMaxN, 0);

ways[kOffset] = 1;

for (int num : nums) {

vector<int> tmp(kMaxN, 0);

for (int i = 0; i < kMaxN; ++i) {

if (i + num < kMaxN) tmp[i] += ways[i + num];

if (i - num >= 0) tmp[i] += ways[i - num];

}

std::swap(ways, tmp);

}

return ways[S + kOffset];

}

};

Solution 2: DFS

Time complexity: O(2^n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 422 ms

class Solution {

public:

int findTargetSumWays(vector<int>& nums, int S) {

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum < std::abs(S)) return 0;

int ans = 0;

dfs(nums, 0, S, ans);

return ans;

}

private:

void dfs(const vector<int>& nums, int d, int S, int& ans) {

if (d == nums.size()) {

if (S == 0) ++ans;

return;

}

dfs(nums, d + 1, S - nums[d], ans);

dfs(nums, d + 1, S + nums[d], ans);

}

};

Java

// Author: Huahua

// Running time: 615 ms

class Solution {

private int ans;

public int findTargetSumWays(int[] nums, int S) {

int sum = 0;

for (final int num : nums)

sum += num;

if (sum < Math.abs(S)) return 0;

ans = 0;

dfs(nums, 0, S);

return ans;

}

private void dfs(int[] nums, int d, int S) {

if (d == nums.length) {

if (S == 0) ++ans;

return;

}

dfs(nums, d + 1, S - nums[d]);

dfs(nums, d + 1, S + nums[d]);

}

Solution 3: Subset sum

Time complexity: O(n*sum)

Space complexity: O(sum)

C++ w/ copy

// Author: Huahua

// Running time: 7 ms

class Solution {

public:

int findTargetSumWays(vector<int>& nums, int S) {

S = std::abs(S);

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum < S || (S + sum) % 2 != 0) return 0;

const int target = (S + sum) / 2;

vector<int> dp(target + 1, 0);

dp[0] = 1;

for (int num : nums) {

vector<int> tmp(dp);

for (int j = 0; j <= target - num; ++j)

tmp[j + num] += dp[j];

std::swap(dp, tmp);

}

return dp[target];

}

};

C++ w/o copy

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

int findTargetSumWays(vector<int>& nums, int S) {

S = std::abs(S);

const int n = nums.size();

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum < S || (S + sum) % 2 != 0) return 0;

const int target = (S + sum) / 2;

vector<int> dp(target + 1, 0);

dp[0] = 1;

for (int num : nums)

for (int j = target; j >= num; --j)

dp[j] += dp[j - num];

return dp[target];

}

};

花花酱 LeetCode 322. Coin Change

By zxi on January 2, 2018

题目大意：给你一些不同币值的硬币，问你最少需要多少个硬币才能组成amount，假设每种硬币有无穷多个。

Problem:

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)

Example 2:
coins = [2], amount = 3
return -1.

Idea:

DP /knapsack

Solution1:

C++ / DP

Time complexity: O(n*amount^2)

Space complexity: O(amount)

// Author: Huahua

// Running time: 189 ms

class Solution {

public:

int coinChange(vector<int>& coins, int amount) {

vector<int> dp(amount + 1, INT_MAX);

dp[0] = 0;

for (auto coin : coins) {

for (int i = amount - coin; i >= 0; --i)

if (dp[i] != INT_MAX)

for (int k = 1; k * coin + i <= amount; ++k)

dp[i + k * coin] = min(dp[i + k * coin], dp[i] + k);

}

return dp[amount] == INT_MAX ? -1 : dp[amount];

}

};

Solution2:

C++ / DP

Time complexity: O(n*amount)

Space complexity: O(amount)

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

int coinChange(vector<int>& coins, int amount) {

// dp[i] = min coins to make up to amount i

vector<int> dp(amount + 1, INT_MAX);

dp[0] = 0;

for (int coin : coins) {

for (int i = coin; i <= amount; ++i)

if (dp[i - coin] != INT_MAX)

dp[i] = min(dp[i], dp[i - coin] + 1);

}

return dp[amount] == INT_MAX ? -1 : dp[amount];

}

};

Python3

"""

Author: Huahua

Running time: 632 ms beats 90.27%

"""

class Solution:

def coinChange(self, coins, amount):

INVALID = 2**32

dp = [INVALID] * (amount + 1)

dp[0] = 0

for coin in coins:

for i in range(coin, amount + 1):

if dp[i - coin] >= dp[i]: continue

dp[i] = dp[i - coin] + 1

return -1 if dp[amount] == INVALID else dp[amount]

Solution3:

C++ / DFS

Time complexity: O(amount^n/(coin_0*coin_1*…*coin_n))

Space complexity: O(n)

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

int coinChange(vector<int>& coins, int amount) {

// Sort coins in desending order

std::sort(coins.rbegin(), coins.rend());

int ans = INT_MAX;

coinChange(coins, 0, amount, 0, ans);

return ans == INT_MAX ? -1 : ans;

}

private:

void coinChange(const vector<int>& coins,

int s, int amount, int count, int& ans) {

if (amount == 0) {

ans = min(ans, count);

return;

}

if (s == coins.size()) return;

const int coin = coins[s];

for (int k = amount / coin; k >= 0 && count + k < ans; k--)

coinChange(coins, s + 1, amount - k * coin, count + k, ans);

}

};

Python3

"""

Author: Huahua

Running time: 200ms

"""

class Solution:

def coinChange(self, coins, amount):

coins.sort(reverse=True)

INVALID = 10**10

self.ans = INVALID

def dfs(s, amount, count):

if amount == 0:

self.ans = count

return

if s == len(coins): return

coin = coins[s]

for k in range(amount // coin, -1, -1):

if count + k >= self.ans: break

dfs(s + 1, amount - k * coin, count + k)

dfs(0, amount, 0)

return -1 if self.ans == INVALID else self.ans

花花酱 LeetCode 652. Find Duplicate Subtrees

By zxi on December 31, 2017

652. Find Duplicate SubtreesMedium730151FavoriteShare

Given a binary tree, return all duplicate subtrees. For each kind of duplicate subtrees, you only need to return the root node of any one of them.

Two trees are duplicate if they have the same structure with same node values.

Example 1:

The following are two duplicate subtrees:

2
/
4

and

Therefore, you need to return above trees’ root in the form of a list.

Solution 1: Serialization

Time complexity: O(n^2)
Space complexity: O(n^2)

C++

// Author: Huahua

// Runtime: 29 ms

class Solution {

public:

vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {

unordered_map<string, int> counts;

vector<TreeNode*> ans;

serialize(root, counts, ans);

return ans;

}

private:

string serialize(TreeNode* root, unordered_map<string, int>& counts, vector<TreeNode*>& ans) {

if (!root) return "#";

string key = to_string(root->val) + ","

+ serialize(root->left, counts, ans) + ","

+ serialize(root->right, counts, ans);

if (++counts[key] == 2)

ans.push_back(root);

return key;

}

};

Solution 2: int id for each unique subtree

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

// Runtime: 8 ms

class Solution {

public:

vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {

unordered_map<long, pair<int,int>> counts;

vector<TreeNode*> ans;

getId(root, counts, ans);

return ans;

}

private:

int getId(TreeNode* root,

unordered_map<long, pair<int,int>>& counts,

vector<TreeNode*>& ans) {

if (!root) return 0;

long key = (static_cast<long>(static_cast<unsigned>(root->val)) << 32) +

(getId(root->left, counts, ans) << 16) +

getId(root->right, counts, ans);

auto& p = counts[key];

if (p.second++ == 0)

p.first = counts.size();

else if (p.second == 2)

ans.push_back(root);

return p.first;

}

};