Posts published in “Queue”

花花酱 LeetCode 1508. Range Sum of Sorted Subarray Sums

By zxi on July 11, 2020

Given the array nums consisting of n positive integers. You computed the sum of all non-empty continous subarrays from the array and then sort them in non-decreasing order, creating a new array of n * (n + 1) / 2 numbers.

Return the sum of the numbers from index left to index right (indexed from 1), inclusive, in the new array. Since the answer can be a huge number return it modulo 10^9 + 7.

Example 1:

Input: nums = [1,2,3,4], n = 4, left = 1, right = 5
Output: 13 
Explanation: All subarray sums are 1, 3, 6, 10, 2, 5, 9, 3, 7, 4. After sorting them in non-decreasing order we have the new array [1, 2, 3, 3, 4, 5, 6, 7, 9, 10]. The sum of the numbers from index le = 1 to ri = 5 is 1 + 2 + 3 + 3 + 4 = 13.

Example 2:

Input: nums = [1,2,3,4], n = 4, left = 3, right = 4
Output: 6
Explanation: The given array is the same as example 1. We have the new array [1, 2, 3, 3, 4, 5, 6, 7, 9, 10]. The sum of the numbers from index le = 3 to ri = 4 is 3 + 3 = 6.

Example 3:

Input: nums = [1,2,3,4], n = 4, left = 1, right = 10
Output: 50

Constraints:

1 <= nums.length <= 10^3
nums.length == n
1 <= nums[i] <= 100
1 <= left <= right <= n * (n + 1) / 2

Solution 1: Brute Force

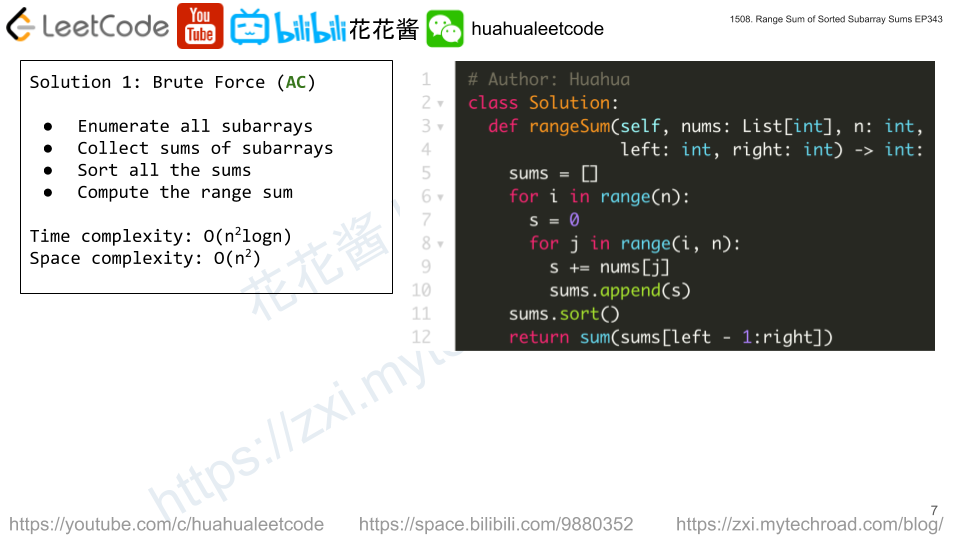
Find sums of all the subarrays and sort the values.

Time complexity: O(n^2logn)
Space complexity: O(n^2)

C++

// Author: Huahua

class Solution {

public:

int rangeSum(vector<int>& nums, int n, int left, int right) {

constexpr int kMod = 1e9 + 7;

vector<int> sums;

for (int i = 0; i < n; ++i)

for (int j = i, sum = 0; j < n; ++j)

sums.push_back(sum += nums[j]);

sort(begin(sums), end(sums));

return accumulate(begin(sums) + left - 1, begin(sums) + right, 0LL) % kMod;

}

};

Java

// Author: Huahua

class Solution {

public int rangeSum(int[] nums, int n, int left, int right) {

final int kMod = (int)(1e9 + 7);

int[] sums = new int[n * (n + 1) / 2];

int idx = 0;

for (int i = 0; i < n; ++i)

for (int j = i, sum = 0; j < n; ++j, ++idx)

sums[idx] = sum += nums[j];

Arrays.sort(sums);

int ans = 0;

for (int i = left; i <= right; ++i)

ans = (ans + sums[i - 1]) % kMod;

return ans;

}

Python3

# Author: Huahua

class Solution:

def rangeSum(self, nums: List[int], n: int, left: int, right: int) -> int:

sums = []

for i in range(n):

s = 0

for j in range(i, n):

s += nums[j]

sums.append(s)

sums.sort()

return sum(sums[left - 1:right])

Solution 2: Priority Queue / Min Heap

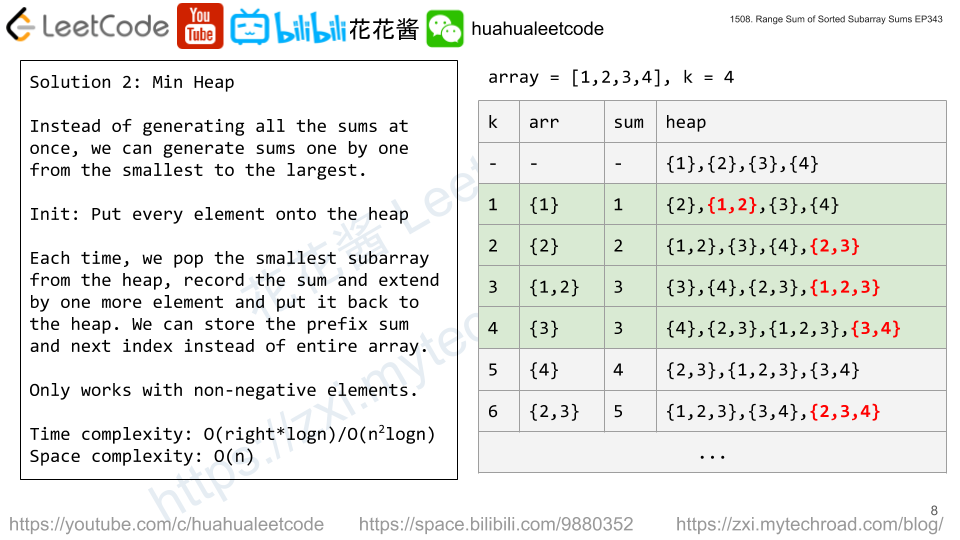
For each subarray, start with one element e.g nums[i], put them into a priority queue (min heap). Each time, we have the smallest subarray sum, and extend that subarray and put the new sum back into priority queue. Thought it has the same time complexity as the brute force one in worst case, but space complexity can be reduce to O(n).

Time complexity: O(n^2logn)
Space complexity: O(n)

C++

struct Entry {

int sum;

int i;

bool operator<(const Entry& e) const { return sum > e.sum; }

};

class Solution {

public:

int rangeSum(vector<int>& nums, int n, int left, int right) {

constexpr int kMod = 1e9 + 7;

priority_queue<Entry> q; // Sort by e.sum in descending order.

for (int i = 0; i < n; ++i)

q.push({nums[i], i});

long ans = 0;

for (int j = 1; j <= right; ++j) {

const auto e = std::move(q.top()); q.pop();

if (j >= left) ans += e.sum;

if (e.i + 1 < n) q.push({e.sum + nums[e.i + 1], e.i + 1});

}

return ans % kMod;

}

};

Java

import java.util.AbstractMap;

class Solution {

public int rangeSum(int[] nums, int n, int left, int right) {

final int kMod = (int)(1e9 + 7);

var q = new PriorityQueue<Map.Entry<Integer, Integer>>((a, b) -> a.getKey() - b.getKey());

for (int i = 0; i < n; ++i)

q.offer(new AbstractMap.SimpleEntry<>(nums[i], i));

int ans = 0;

for (int k = 1; k <= right; ++k) {

var e = q.poll();

int sum = e.getKey();

int i = e.getValue();

if (k >= left)

ans = (ans + sum) % kMod;

if (i + 1 < n)

q.offer(new AbstractMap.SimpleEntry<>(sum + nums[i + 1], i + 1));

}

return ans;

}

Python3

# Author: Huahua

class Solution:

def rangeSum(self, nums: List[int], n: int, left: int, right: int) -> int:

q = [(num, i) for i, num in enumerate(nums)]

heapq.heapify(q)

ans = 0

for k in range(1, right + 1):

s, i = heapq.heappop(q)

if k >= left:

ans += s

if i + 1 < n:

heapq.heappush(q, (s + nums[i + 1], i + 1))

return ans % int(1e9 + 7)

Solution 3: Binary Search + Sliding Window

Use binary search to find S s.t. that there are at least k subarrys have sum <= S.

Given S, we can use sliding window to count how many subarrays have sum <= S and their total sum.

ans = sums_of_first(right) – sums_of_first(left – 1).

Time complexity: O(n * log(sum(nums))
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int rangeSum(vector<int>& nums, int n, int left, int right) {

constexpr int kMod = 1e9 + 7;

// Returns number of subarrays that have

// sum <= target and their total sum.

auto countAndSum = [&](int target) -> pair<int, long> {

int count = 0;

long cur = 0;

long sum = 0;

long total_sum = 0;

for (long j = 0, i = 0; j < n; ++j) {

cur += nums[j];

sum += nums[j] * (j - i + 1);

while (cur > target) {

sum -= cur;

cur -= nums[i++];

}

count += j - i + 1;

total_sum += sum;

}

return {count, total_sum};

};

// Returns the total sums of smallest k subarrays.

// Use binary search to find the smallest sum l s.t.

// there are at least k of subarrays have sums <= l.

const int min_sum = *min_element(begin(nums), end(nums));

const int max_sum = accumulate(begin(nums), end(nums), 0) + 1;

auto sumOfFirstK = [&](int k) -> long {

int l = min_sum;

int r = max_sum;

while (l < r) {

int mid = l + (r - l) / 2;

if (countAndSum(mid).first >= k)

r = mid;

else

l = mid + 1;

}

const auto [count, sum] = countAndSum(l);

// There can be more subarrays have the same sum of l.

return sum - l * (count - k);

};

return (sumOfFirstK(right) - sumOfFirstK(left - 1)) % kMod;

}

};

花花酱 LeetCode 1499. Max Value of Equation

By zxi on June 28, 2020

Given an array points containing the coordinates of points on a 2D plane, sorted by the x-values, where points[i] = [x_i, y_i] such that x_i < x_j for all 1 <= i < j <= points.length. You are also given an integer k.

Example 1:

Input: points = [[1,3],[2,0],[5,10],[6,-10]], k = 1
Output: 4
Explanation: The first two points satisfy the condition |x_i - x_j| <= 1 and if we calculate the equation we get 3 + 0 + |1 - 2| = 4. Third and fourth points also satisfy the condition and give a value of 10 + -10 + |5 - 6| = 1.
No other pairs satisfy the condition, so we return the max of 4 and 1.

Example 2:

Input: points = [[0,0],[3,0],[9,2]], k = 3
Output: 3
Explanation: Only the first two points have an absolute difference of 3 or less in the x-values, and give the value of 0 + 0 + |0 - 3| = 3.

Constraints:

2 <= points.length <= 10^5
points[i].length == 2
-10^8 <= points[i][0], points[i][1] <= 10^8
0 <= k <= 2 * 10^8
points[i][0] < points[j][0] for all 1 <= i < j <= points.length
x_i form a strictly increasing sequence.

Observation

Since xj > xi, so |xi – xj| + yi + yj => xj + yj + (yi – xi)
We want to have yi – xi as large as possible while need to make sure xj – xi <= k.

Solution 1: Priority Queue / Heap

Put all the points processed so far onto the heap as (y-x, x) sorted by y-x in descending order.
Each new point (x_j, y_j), find the largest y-x such that x_j – x <= k.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int findMaxValueOfEquation(vector<vector<int>>& points, int k) {

priority_queue<pair<int, int>> q; // {y - x, x}

q.emplace(0, -1e9);

int ans = INT_MIN;

for (const auto& p : points) {

const int x = p[0], y = p[1];

while (!q.empty() && x - q.top().second > k) q.pop();

if (!q.empty())

ans = max(ans, x + y + q.top().first);

q.emplace(y - x, x);

}

return ans;

}

};

Solution 2: Monotonic Queue

Maintain a monotonic queue:
1. The queue is sorted by y – x in descending order.
2. Pop then front element when xj – x_front > k, they can’t be used anymore.
3. Record the max of {xj + yj + (y_front – x_front)}
4. Pop the back element when yj – xj > y_back – x_back, they are smaller and lefter. Won’t be useful anymore.
5. Finally, push the j-th element onto the queue.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int findMaxValueOfEquation(vector<vector<int>>& points, int k) {

deque<pair<int, int>> q; // {y - x, x} Sort by y - x.

int ans = INT_MIN;

for (const auto& p : points) {

const int xj = p[0];

const int yj = p[1];

// Remove invalid points, e.g. xj - xi > k

while (!q.empty() && xj - q.front().second > k)

q.pop_front();

if (!q.empty())

ans = max(ans, xj + yj + q.front().first);

while (!q.empty() && yj - xj >= q.back().first)

q.pop_back();

q.emplace_back(yj - xj, xj);

}

return ans;

}

};

Java

class Solution {

public int findMaxValueOfEquation(int[][] points, int k) {

var q = new ArrayDeque<Integer>();

int ans = Integer.MIN_VALUE;

for (int i = 0; i < points.length; ++i) {

int xj = points[i][0];

int yj = points[i][1];

while (!q.isEmpty() && xj - points[q.getFirst()][0] > k) {

q.removeFirst();

}

if (!q.isEmpty()) {

ans = Math.max(ans, xj + yj

+ points[q.getFirst()][1] - points[q.getFirst()][0]);

}

while (!q.isEmpty() && yj - xj

>= points[q.getLast()][1] - points[q.getLast()][0]) {

q.removeLast();

}

q.offer(i);

}

return ans;

}

python3

# Author: Huahua

class Solution:

def findMaxValueOfEquation(self, points: List[List[int]], k: int) -> int:

ans = float('-inf')

q = deque() # {(y - x, x)}

for x, y in points:

while q and x - q[0][1] > k: q.popleft()

if q: ans = max(ans, x + y + q[0][0])

while q and y - x >= q[-1][0]: q.pop()

q.append((y - x, x))

return ans

花花酱 LeetCode 1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit

By zxi on May 3, 2020

Given an array of integers nums and an integer limit, return the size of the longest continuous subarray such that the absolute difference between any two elements is less than or equal to limit.

In case there is no subarray satisfying the given condition return 0.

Example 1:

Input: nums = [8,2,4,7], limit = 4
Output: 2 
Explanation: All subarrays are: 
[8] with maximum absolute diff |8-8| = 0 <= 4.
[8,2] with maximum absolute diff |8-2| = 6 > 4. 
[8,2,4] with maximum absolute diff |8-2| = 6 > 4.
[8,2,4,7] with maximum absolute diff |8-2| = 6 > 4.
[2] with maximum absolute diff |2-2| = 0 <= 4.
[2,4] with maximum absolute diff |2-4| = 2 <= 4.
[2,4,7] with maximum absolute diff |2-7| = 5 > 4.
[4] with maximum absolute diff |4-4| = 0 <= 4.
[4,7] with maximum absolute diff |4-7| = 3 <= 4.
[7] with maximum absolute diff |7-7| = 0 <= 4. 
Therefore, the size of the longest subarray is 2.

Example 2:

Input: nums = [10,1,2,4,7,2], limit = 5
Output: 4 
Explanation: The subarray [2,4,7,2] is the longest since the maximum absolute diff is |2-7| = 5 <= 5.

Example 3:

Input: nums = [4,2,2,2,4,4,2,2], limit = 0
Output: 3

Constraints:

1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
0 <= limit <= 10^9

Solution 1: Sliding Window + TreeSet

Use a treeset to maintain a range of [l, r] such that max(nums[l~r]) – min(nums[l~r]) <= limit.
Every time, we add nums[r] into the tree, and move l towards r to keep the max diff under limit.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int longestSubarray(vector<int>& nums, int limit) {

multiset<int> s;

int l = 0;

int ans = 0;

for (int r = 0; r < nums.size(); ++r) {

s.insert(nums[r]);

while (*rbegin(s) - *begin(s) > limit)

s.erase(s.equal_range(nums[l++]).first);

ans = max(ans, r - l + 1);

}

return ans;

}

};

Solution 2: Dual Monotonic Queue

We want to maintain a range [l, r] that max(nums[l~r]) – min(nums[l~r]) <= limit, to track the max/min of a range efficiently we could use monotonic queue. One for max and one for min.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int longestSubarray(vector<int>& nums, int limit) {

deque<int> max_q;

deque<int> min_q;

int ans = 0;

int l = 0;

for (int r = 0; r < nums.size(); ++r) {

while (!min_q.empty() && nums[r] < min_q.back())

min_q.pop_back();

while (!max_q.empty() && nums[r] > max_q.back())

max_q.pop_back();

min_q.push_back(nums[r]);

max_q.push_back(nums[r]);

while (max_q.front() - min_q.front() > limit) {

if (max_q.front() == nums[l]) max_q.pop_front();

if (min_q.front() == nums[l]) min_q.pop_front();

++l;

}

ans = max(ans, r - l + 1);

}

return ans;

}

};

花花酱 LeetCode 933. Number of Recent Calls

By zxi on November 4, 2018

Problem

Write a class RecentCounter to count recent requests.

It has only one method: ping(int t), where t represents some time in milliseconds.

Return the number of pings that have been made from 3000 milliseconds ago until now.

Any ping with time in [t - 3000, t] will count, including the current ping.

It is guaranteed that every call to ping uses a strictly larger value of t than before.

Example 1:

Input: inputs = ["RecentCounter","ping","ping","ping","ping"], inputs = [[],[1],[100],[3001],[3002]]
Output: [null,1,2,3,3]

Note:

Each test case will have at most 10000 calls to ping.
Each test case will call ping with strictly increasing values of t.
Each call to ping will have 1 <= t <= 10^9.

Solution: Queue

Use a FIFO queue to track all the previous pings that are within 3000 ms to current.

Time complexity: Avg O(1), Total O(n)

Space complexity: O(n)

C++

class RecentCounter {

public:

RecentCounter() {}

int ping(int t) {

while (!q.empty() && t - q.front() > 3000) q.pop();

q.push(t);

return q.size();

}

private:

queue<int> q;

};