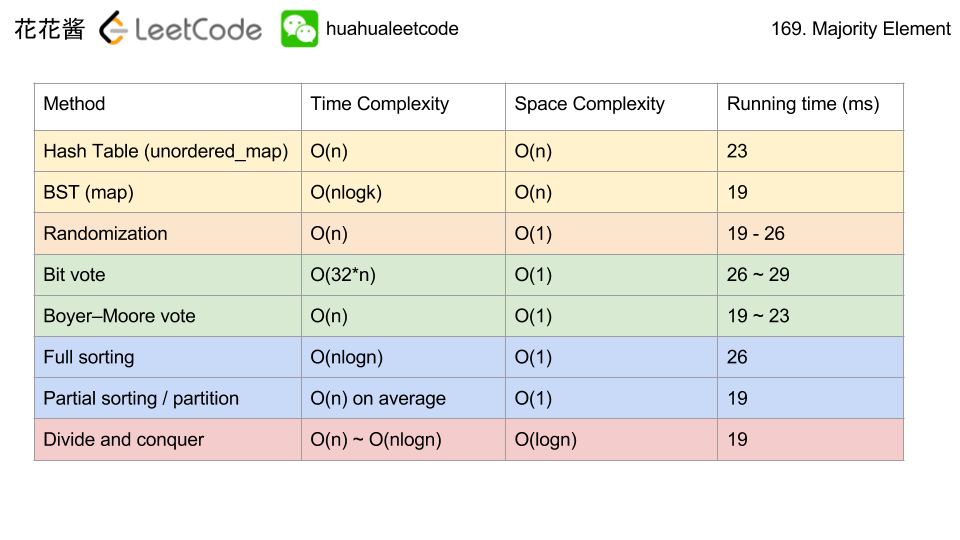
(This problem is an interactive problem.)
On the sea represented by a cartesian plane, each ship is located at an integer point, and each integer point may contain at most 1 ship.
You have a function Sea.hasShips(topRight, bottomLeft) which takes two points as arguments and returns true if and only if there is at least one ship in the rectangle represented by the two points, including on the boundary.
Given two points, which are the top right and bottom left corners of a rectangle, return the number of ships present in that rectangle. It is guaranteed that there are at most 10 ships in that rectangle.
Submissions making more than 400 calls to hasShips will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.
Example :
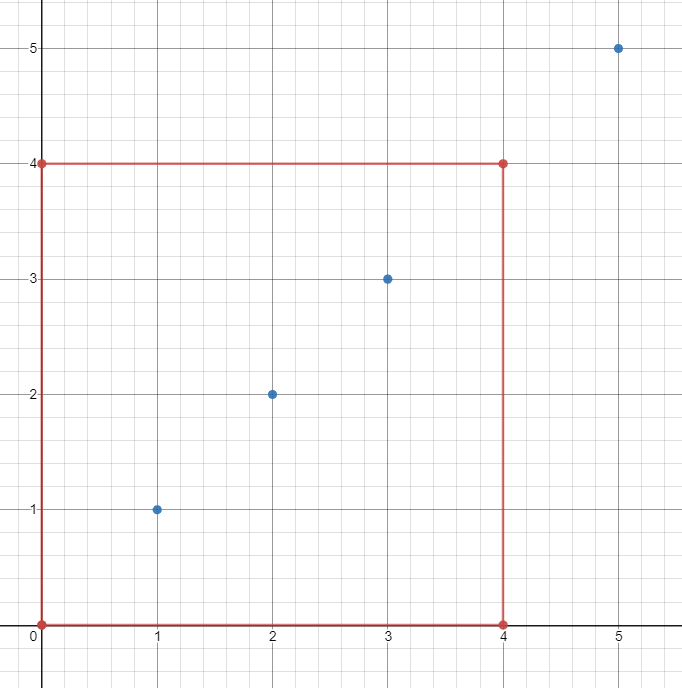
Input: ships = [[1,1],[2,2],[3,3],[5,5]], topRight = [4,4], bottomLeft = [0,0] Output: 3 Explanation: From [0,0] to [4,4] we can count 3 ships within the range.
Constraints:
- On the input
shipsis only given to initialize the map internally. You must solve this problem “blindfolded”. In other words, you must find the answer using the givenhasShipsAPI, without knowing theshipsposition. 0 <= bottomLeft[0] <= topRight[0] <= 10000 <= bottomLeft[1] <= topRight[1] <= 1000
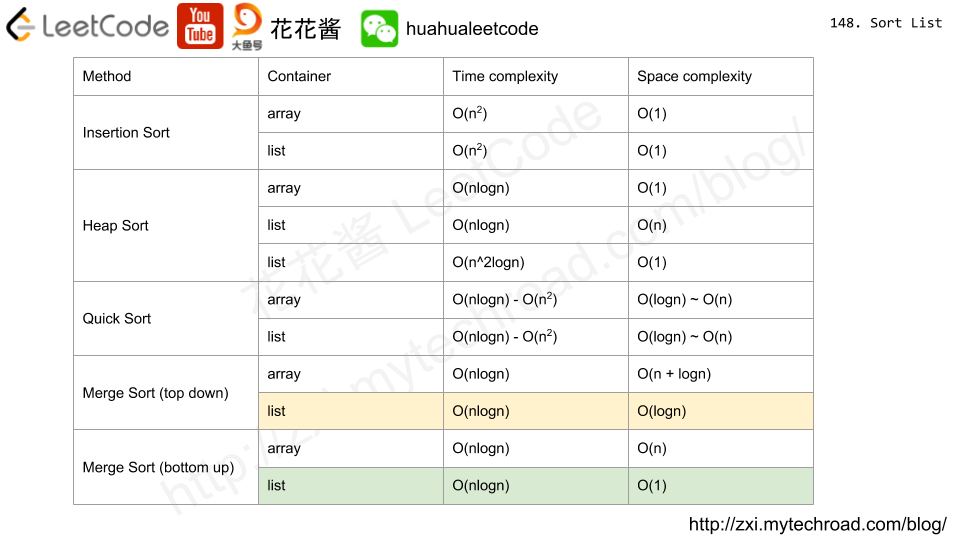
Solution: Divide and Conquer
If the current rectangle contains ships, subdivide it into 4 smaller ones until
1) no ships contained
2) the current rectangle is a single point (e.g. topRight == bottomRight)
Time complexity: O(logn)
Space complexity: O(logn)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
// Author: Huahua class Solution { public: // Modify the interface to pass sea as a reference. int countShips(Sea& sea, vector<int> topRight, vector<int> bottomLeft) { int x1 = bottomLeft[0], y1 = bottomLeft[1]; int x2 = topRight[0], y2 = topRight[1]; if (x1 > x2 || y1 > y2 || !sea.hasShips(topRight, bottomLeft)) return 0; if (x1 == x2 && y1 == y2) return 1; int xm = x1 + (x2 - x1) / 2; int ym = y1 + (y2 - y1) / 2; return countShips(sea, {xm, ym}, {x1, y1}) + countShips(sea, {xm, y2}, {x1, ym + 1}) + countShips(sea, {x2, ym}, {xm + 1, y1}) + countShips(sea, {x2, y2}, {xm + 1, ym + 1}); } }; |