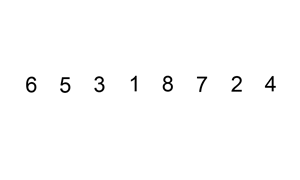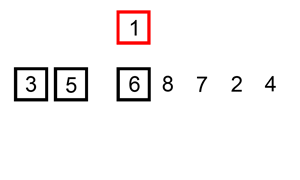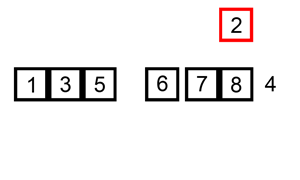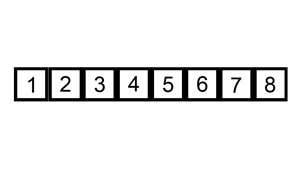Press "Enter" to skip to content

Posts published in “List”

花花酱 LeetCode 430. Flatten a Multilevel Doubly Linked List

By zxi on April 5, 2025

用递归实现比较简单一点。如果需要完美的one pass则需要写一个helper function，返回flattern后的head和tail.

注意这是双向链表，要把A把B连接到一起，需要同时改两个指针A->next = B, B->prev = A。

时间复杂度：O(n)
空间复杂度：O(n) / stack

花花酱 LeetCode 2181. Merge Nodes in Between Zeros

By zxi on March 2, 2022

You are given the head of a linked list, which contains a series of integers separated by 0‘s. The beginning and end of the linked list will have Node.val == 0.

For every two consecutive 0‘s, merge all the nodes lying in between them into a single node whose value is the sum of all the merged nodes. The modified list should not contain any 0‘s.

Return the head of the modified linked list.

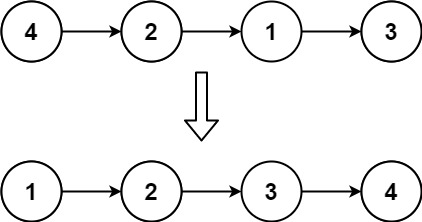
Example 1:

Input: head = [0,3,1,0,4,5,2,0]
Output: [4,11]
Explanation: 
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 3 + 1 = 4.
- The sum of the nodes marked in red: 4 + 5 + 2 = 11.

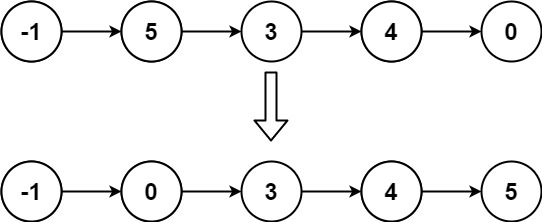
Example 2:

Input: head = [0,1,0,3,0,2,2,0]
Output: [1,3,4]
Explanation: 
The above figure represents the given linked list. The modified list contains
- The sum of the nodes marked in green: 1 = 1.
- The sum of the nodes marked in red: 3 = 3.
- The sum of the nodes marked in yellow: 2 + 2 = 4.

Constraints:

  • The number of nodes in the list is in the range [3, 2 * 105].
  • 0 <= Node.val <= 1000
  • There are no two consecutive nodes with Node.val == 0.
  • The beginning and end of the linked list have Node.val == 0.

Solution: List

Skip the first zero, replace every zero node with the sum of values of its previous nodes.

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 2130. Maximum Twin Sum of a Linked List

By zxi on January 9, 2022

In a linked list of size n, where n is even, the ith node (0-indexed) of the linked list is known as the twin of the (n-1-i)th node, if 0 <= i <= (n / 2) - 1.

  • For example, if n = 4, then node 0 is the twin of node 3, and node 1 is the twin of node 2. These are the only nodes with twins for n = 4.

The twin sum is defined as the sum of a node and its twin.

Given the head of a linked list with even length, return the maximum twin sum of the linked list.

Example 1:

Input: head = [5,4,2,1]
Output: 6
Explanation:
Nodes 0 and 1 are the twins of nodes 3 and 2, respectively. All have twin sum = 6.
There are no other nodes with twins in the linked list.
Thus, the maximum twin sum of the linked list is 6.

Example 2:

Input: head = [4,2,2,3]
Output: 7
Explanation:
The nodes with twins present in this linked list are:
- Node 0 is the twin of node 3 having a twin sum of 4 + 3 = 7.
- Node 1 is the twin of node 2 having a twin sum of 2 + 2 = 4.
Thus, the maximum twin sum of the linked list is max(7, 4) = 7.

Example 3:

Input: head = [1,100000]
Output: 100001
Explanation:
There is only one node with a twin in the linked list having twin sum of 1 + 100000 = 100001.

Constraints:

  • The number of nodes in the list is an even integer in the range [2, 105].
  • 1 <= Node.val <= 105

Solution: Two Pointers + Reverse List

Use fast slow pointers to find the middle point and reverse the second half.

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 2095. Delete the Middle Node of a Linked List

By zxi on December 4, 2021

You are given the head of a linked list. Delete the middle node, and return the head of the modified linked list.

The middle node of a linked list of size n is the ⌊n / 2⌋th node from the start using 0-based indexing, where ⌊x⌋ denotes the largest integer less than or equal to x.

  • For n = 1, 2, 3, 4, and 5, the middle nodes are 0, 1, 1, 2, and 2, respectively.

Example 1:

Input: head = [1,3,4,7,1,2,6]
Output: [1,3,4,1,2,6]
Explanation:
The above figure represents the given linked list. The indices of the nodes are written below.
Since n = 7, node 3 with value 7 is the middle node, which is marked in red.
We return the new list after removing this node.

Example 2:

Input: head = [1,2,3,4]
Output: [1,2,4]
Explanation:
The above figure represents the given linked list.
For n = 4, node 2 with value 3 is the middle node, which is marked in red.

Example 3:

Input: head = [2,1]
Output: [2]
Explanation:
The above figure represents the given linked list.
For n = 2, node 1 with value 1 is the middle node, which is marked in red.
Node 0 with value 2 is the only node remaining after removing node 1.

Constraints:

  • The number of nodes in the list is in the range [1, 105].
  • 1 <= Node.val <= 105

Solution: Fast / Slow pointers

Use fast / slow pointers to find the previous node of the middle one, then skip the middle one.

prev.next = prev.next.next

Time complexity: O(n)
Space complexity: O(1)

C++

花花酱 LeetCode 143. Reorder List

By zxi on November 28, 2021

You are given the head of a singly linked-list. The list can be represented as:

L0 → L1 → … → Ln - 1 → Ln

Reorder the list to be on the following form:

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …

You may not modify the values in the list’s nodes. Only nodes themselves may be changed.

Example 1:

Input: head = [1,2,3,4]
Output: [1,4,2,3]

Example 2:

Input: head = [1,2,3,4,5]
Output: [1,5,2,4,3]

Constraints:

  • The number of nodes in the list is in the range [1, 5 * 104].
  • 1 <= Node.val <= 1000

Solution: Three steps

Step 1: Find mid node that splits the list into two halves.
Step 2: Reverse the second half
Step 3: Merge two lists

Time complexity: O(n)
Space complexity: O(1)

C++