Posts tagged as “dp”

花花酱 LeetCode 2771. Longest Non-decreasing Subarray From Two Arrays

By zxi on July 15, 2023

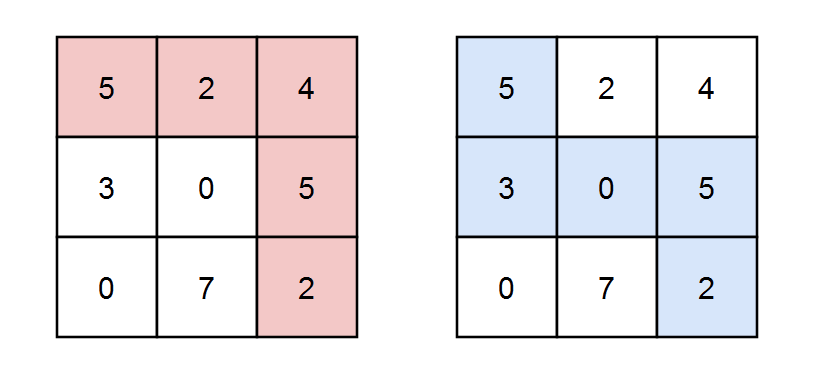
You are given two 0-indexed integer arrays nums1 and nums2 of length n.

Let’s define another 0-indexed integer array, nums3, of length n. For each index i in the range [0, n - 1], you can assign either nums1[i] or nums2[i] to nums3[i].

Your task is to maximize the length of the longest non-decreasing subarray in nums3 by choosing its values optimally.

Return an integer representing the length of the longest non-decreasing subarray in nums3.

Note: A subarray is a contiguous non-empty sequence of elements within an array.

Example 1:

Input: nums1 = [2,3,1], nums2 = [1,2,1]
Output: 2
Explanation: One way to construct nums3 is: 
nums3 = [nums1[0], nums2[1], nums2[2]] => [2,2,1]. 
The subarray starting from index 0 and ending at index 1, [2,2], forms a non-decreasing subarray of length 2. 
We can show that 2 is the maximum achievable length.

Example 2:

Input: nums1 = [1,3,2,1], nums2 = [2,2,3,4]
Output: 4
Explanation: One way to construct nums3 is: 
nums3 = [nums1[0], nums2[1], nums2[2], nums2[3]] => [1,2,3,4]. 
The entire array forms a non-decreasing subarray of length 4, making it the maximum achievable length.

Example 3:

Input: nums1 = [1,1], nums2 = [2,2]
Output: 2
Explanation: One way to construct nums3 is: 
nums3 = [nums1[0], nums1[1]] => [1,1]. 
The entire array forms a non-decreasing subarray of length 2, making it the maximum achievable length.

Constraints:

1 <= nums1.length == nums2.length == n <= 10⁵
1 <= nums1[i], nums2[i] <= 10⁹

Solution: DP

Let dp1(i), dp2(i) denote the length of the Longest Non-decreasing Subarray ends with nums1[i] and nums2[i] respectively.

init: dp1(0) = dp2(0) = 1

dp1(i) = max(dp1(i – 1) + 1 if nums1[i] >= nums1[i – 1] else 1, dp2(i – 1) + 1 if nums1[i] >= nums2[i – 1] else 1)
dp2(i) = max(dp1(i – 1) + 1 if nums2[i] >= nums1[i – 1] else 1, dp2(i – 1) + 1 if nums2[i] >= nums2[i – 1] else 1)

ans = max(dp1, dp2)

Time complexity: O(n)
Space complexity: O(n) -> O(1)

Python3

# Author: Huahua

class Solution:

def maxNonDecreasingLength(self, nums1: List[int], nums2: List[int]) -> int:

n = len(nums1)

nums = [nums1, nums2]

@cache

def dp(i: int, j: int):

if i == 0: return 1

ans = 1

for k in range(2):

if nums[j][i] >= nums[k][i - 1]:

ans = max(ans, dp(i - 1, k) + 1)

return ans

return max(max(dp(i, 0), dp(i, 1)) for i in range(n))

C++

// Author: Huahua

class Solution {

public:

int maxNonDecreasingLength(vector<int>& nums1, vector<int>& nums2) {

int ans = 1;

for (int i = 1, dp1 = 1, dp2 = 1; i < nums1.size(); ++i) {

int t1 = max(nums1[i] >= nums1[i - 1] ? dp1 + 1 : 1,

nums1[i] >= nums2[i - 1] ? dp2 + 1 : 1);

int t2 = max(nums2[i] >= nums1[i - 1] ? dp1 + 1 : 1,

nums2[i] >= nums2[i - 1] ? dp2 + 1 : 1);

dp1 = t1;

dp2 = t2;

ans = max({ans, dp1, dp2});

}

return ans;

}

};

花花酱 LeetCode 2770. Maximum Number of Jumps to Reach the Last Index

By zxi on July 11, 2023

You are given a 0-indexed array nums of n integers and an integer target.

You are initially positioned at index 0. In one step, you can jump from index i to any index j such that:

0 <= i < j < n
-target <= nums[j] - nums[i] <= target

Return the maximum number of jumps you can make to reach index n - 1.

If there is no way to reach index n - 1, return -1.

Example 1:

Input: nums = [1,3,6,4,1,2], target = 2
Output: 3
Explanation: To go from index 0 to index n - 1 with the maximum number of jumps, you can perform the following jumping sequence:
- Jump from index 0 to index 1. 
- Jump from index 1 to index 3.
- Jump from index 3 to index 5.
It can be proven that there is no other jumping sequence that goes from 0 to n - 1 with more than 3 jumps. Hence, the answer is 3.

Example 2:

Input: nums = [1,3,6,4,1,2], target = 3
Output: 5
Explanation: To go from index 0 to index n - 1 with the maximum number of jumps, you can perform the following jumping sequence:
- Jump from index 0 to index 1.
- Jump from index 1 to index 2.
- Jump from index 2 to index 3.
- Jump from index 3 to index 4.
- Jump from index 4 to index 5.
It can be proven that there is no other jumping sequence that goes from 0 to n - 1 with more than 5 jumps. Hence, the answer is 5.

Example 3:

Input: nums = [1,3,6,4,1,2], target = 0
Output: -1
Explanation: It can be proven that there is no jumping sequence that goes from 0 to n - 1. Hence, the answer is -1.

Constraints:

2 <= nums.length == n <= 1000
-10⁹ <= nums[i] <= 10⁹
0 <= target <= 2 * 10⁹

Solution: DP

Let dp(i) denotes the maximum jumps from index i to index n-1.

For each index i, try jumping to all possible index j.

dp(i) = max(1 + dp(j)) if j > i and abs(nums[j] – nums[i) <= target else -1

Time complexity: O(n²)
Space complexity: O(n)

Python3

# Author: Huahua

class Solution:

def maximumJumps(self, nums: List[int], target: int) -> int:

n = len(nums)

@cache

def dp(i):

if i == n - 1: return 0

ans = -1

for j in range(i + 1, n):

if abs(nums[j] - nums[i]) <= target and dp(j) != -1:

ans = max(ans, 1 + dp(j))

return ans

return dp(0)

花花酱 LeetCode 2560. House Robber IV

By zxi on February 4, 2023

There are several consecutive houses along a street, each of which has some money inside. There is also a robber, who wants to steal money from the homes, but he refuses to steal from adjacent homes.

The capability of the robber is the maximum amount of money he steals from one house of all the houses he robbed.

You are given an integer array nums representing how much money is stashed in each house. More formally, the i^th house from the left has nums[i] dollars.

You are also given an integer k, representing the minimum number of houses the robber will steal from. It is always possible to steal at least k houses.

Return the minimum capability of the robber out of all the possible ways to steal at least k houses.

Example 1:

Input: nums = [2,3,5,9], k = 2
Output: 5
Explanation: 
There are three ways to rob at least 2 houses:
- Rob the houses at indices 0 and 2. Capability is max(nums[0], nums[2]) = 5.
- Rob the houses at indices 0 and 3. Capability is max(nums[0], nums[3]) = 9.
- Rob the houses at indices 1 and 3. Capability is max(nums[1], nums[3]) = 9.
Therefore, we return min(5, 9, 9) = 5.

Example 2:

Input: nums = [2,7,9,3,1], k = 2
Output: 2
Explanation: There are 7 ways to rob the houses. The way which leads to minimum capability is to rob the house at index 0 and 4. Return max(nums[0], nums[4]) = 2.

Constraints:

1 <= nums.length <= 10⁵
1 <= nums[i] <= 10⁹
1 <= k <= (nums.length + 1)/2

Solution 1: Binary Search + DP

It’s easy to see that higher capability means more houses we can rob. Thus this can be formulate as a binary search algorithm e.g. find the minimum C s.t. we can rob at least k houses.

Then we can use dp(i) to calculate maximum houses we can rob if starting from the i’th house.
dp(i) = max(1 + dp(i + 2) if nums[i] <= C else 0, dp(i + 1))

Time complexity: O(n log m)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int minCapability(vector<int>& nums, int k) {

int l = 0;

int r = *max_element(begin(nums), end(nums)) + 1;

vector<int> cache(nums.size(), -1);

function<int(int, int)> rob = [&](int m, int i) -> int {

if (i >= nums.size()) return 0;

if (cache[i] >= 0) return cache[i];

if (nums[i] > m) return rob(m, i + 1);

return cache[i] = max(1 + rob(m, i + 2), rob(m, i + 1));

};

while (l < r) {

int m = l + (r - l) / 2;

fill(begin(cache), end(cache), -1);

if (rob(m, 0) >= k)

r = m;

else

l = m + 1;

}

return l;

}

};

Solution 2: Binary Search + Greedy

From: dp(i) = max(1 + dp(i + 2) if nums[i] <= C else 0, dp(i + 1)) we can see that if we can pick the i-th one, it will be the same or better if we skip and start from dp(i + 1). Thus we can convert this from DP to greedy. As long as we can pick the current one, we pick it first.

Time complexity: O(n log m)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minCapability(vector<int>& nums, int k) {

int l = 0;

int r = *max_element(begin(nums), end(nums)) + 1;

auto rob = [&](int m) -> int {

int ans = 0;

for (int i = 0; i < nums.size(); ++i)

if (nums[i] <= m) {

++ans;

++i;

}

return ans;

};

while (l < r) {

int m = l + (r - l) / 2;

if (rob(m) >= k)

r = m;

else

l = m + 1;

}

return l;

}

};

花花酱 LeetCode 2435. Paths in Matrix Whose Sum Is Divisible by K

By zxi on October 10, 2022

You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.

Return the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it modulo 10⁹ + 7.

Example 1:

Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
Output: 2
Explanation: There are two paths where the sum of the elements on the path is divisible by k.
The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3.
The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.

Example 2:

Input: grid = [[0,0]], k = 5
Output: 1
Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.

Example 3:

Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
Output: 10
Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 10⁴
1 <= m * n <= 5 * 10⁴
0 <= grid[i][j] <= 100
1 <= k <= 50

Solution: DP

Let dp[i][j][r] := # of paths from (0,0) to (i,j) with path sum % k == r.

init: dp[0][0][grid[0][0] % k] = 1

dp[i][j][(r + grid[i][j]) % k] = dp[i-1][j][r] + dp[i][j-1][r]

ans = dp[m-1][n-1][0]

Time complexity: O(m*n*k)
Space complexity: O(m*n*k) -> O(n*k)

C++

// Author: Huahua

class Solution {

public:

int numberOfPaths(vector<vector<int>>& grid, int k) {

const int kMod = 1e9 + 7;

const int m = grid.size();

const int n = grid[0].size();

vector<vector<vector<int>>> dp(m, vector<vector<int>>(n, vector<int>(k)));

dp[0][0][grid[0][0] % k] = 1;

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j) {

if (i == 0 && j == 0) continue;

for (int r = 0; r < k; ++r)

dp[i][j][(r + grid[i][j]) % k] =

((j ? dp[i][j - 1][r] : 0) + (i ? dp[i - 1][j][r] : 0)) % kMod;

}

return dp[m - 1][n - 1][0];

}

};

花花酱 LeetCode 2420. Find All Good Indices

By zxi on September 26, 2022

You are given a 0-indexed integer array nums of size n and a positive integer k.

We call an index i in the range k <= i < n - k good if the following conditions are satisfied:

The k elements that are just before the index i are in non-increasing order.
The k elements that are just after the index i are in non-decreasing order.

Return an array of all good indices sorted in increasing order.

Example 1:

Input: nums = [2,1,1,1,3,4,1], k = 2
Output: [2,3]
Explanation: There are two good indices in the array:
- Index 2. The subarray [2,1] is in non-increasing order, and the subarray [1,3] is in non-decreasing order.
- Index 3. The subarray [1,1] is in non-increasing order, and the subarray [3,4] is in non-decreasing order.
Note that the index 4 is not good because [4,1] is not non-decreasing.

Example 2:

Input: nums = [2,1,1,2], k = 2
Output: []
Explanation: There are no good indices in this array.

Constraints:

n == nums.length
3 <= n <= 10⁵
1 <= nums[i] <= 10⁶
1 <= k <= n / 2

Solution: Prefix Sum

Let before[i] = length of longest non-increasing subarray ends of nums[i].
Let after[i] = length of longest non-decreasing subarray ends of nums[i].

An index is good if nums[i – 1] >= k and nums[i + k] >= k

Time complexity: O(n + (n – 2*k))
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> goodIndices(vector<int>& nums, int k) {

const int n = nums.size();

vector<int> before(n, 1);

vector<int> after(n, 1);

for (int i = 1; i < n; ++i) {

if (nums[i] <= nums[i - 1])

before[i] = before[i - 1] + 1;

if (nums[i] >= nums[i - 1])

after[i] = after[i - 1] + 1;

}

vector<int> ans;

for (int i = k; i + k < n; ++i) {

if (before[i - 1] >= k && after[i + k] >= k)

ans.push_back(i);

}

return ans;

}

};