Posts published in “Dynamic Programming”

花花酱 LeetCode 1223. Dice Roll Simulation

By zxi on October 17, 2019

A die simulator generates a random number from 1 to 6 for each roll. You introduced a constraint to the generator such that it cannot roll the number i more than rollMax[i] (1-indexed) consecutive times.

Given an array of integers rollMax and an integer n, return the number of distinct sequences that can be obtained with exact n rolls.

Two sequences are considered different if at least one element differs from each other. Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: n = 2, rollMax = [1,1,2,2,2,3]
Output: 34
Explanation: There will be 2 rolls of die, if there are no constraints on the die, there are 6 * 6 = 36 possible combinations. In this case, looking at rollMax array, the numbers 1 and 2 appear at most once consecutively, therefore sequences (1,1) and (2,2) cannot occur, so the final answer is 36-2 = 34.

Example 2:

Input: n = 2, rollMax = [1,1,1,1,1,1]
Output: 30

Example 3:

Input: n = 3, rollMax = [1,1,1,2,2,3]
Output: 181

Constraints:

1 <= n <= 5000
rollMax.length == 6
1 <= rollMax[i] <= 15

Solutions: DP

Naive one:

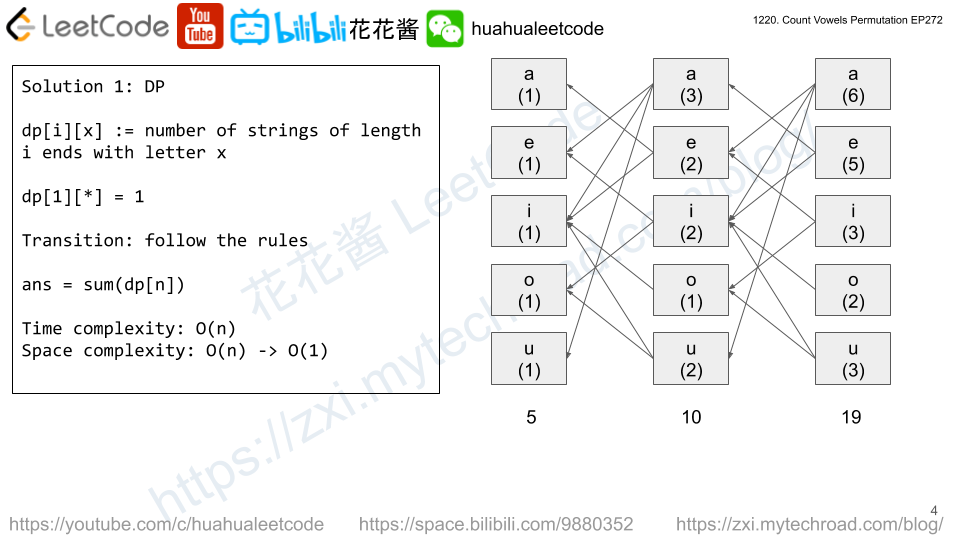
def: dp[i][j][k] := # of sequences ends with k consecutive j after i rolls
Init: dp[1][*][1] = 1

transition:
dp[i][j][1] = sum(dp[i-1][p][*]), p != j
dp[i][j][k + 1] = dp[i-1][j]][k]

Time complexity: O(n*6*6*15)
Space complexity: O(n*6*15) -> O(6*15)

C++

// Author: Huahua

class Solution {

public:

int dieSimulator(int n, vector<int>& rollMax) {

constexpr int kMaxRolls = 15;

constexpr int kMod = 1e9 + 7;

// dp[i][j][k] := # of sequences ends with k consecutive j after i rolls

vector<vector<vector<int>>> dp(n + 1,

vector<vector<int>>(6, vector<int>(kMaxRolls + 1)));

for (int j = 0; j < 6; ++j)

dp[1][j][1] = 1; // 1 step, 1 dice, 1 way

for (int i = 2; i <= n; ++i)

for (int j = 0; j < 6; ++j)

for (int p = 0; p < 6; ++p)

for (int k = 1; k <= rollMax[p]; ++k)

if (p != j) // not the same dice

dp[i][j][1] = (dp[i][j][1] + dp[i - 1][p][k]) % kMod;

else if (k < rollMax[p]) // same dice, make sure k + 1 <= rollMax

dp[i][j][k + 1] = (dp[i][j][k + 1] + dp[i - 1][p][k]) % kMod;

int ans = 0;

for (int j = 0; j < 6; ++j)

for (int k = 1; k <= rollMax[j]; ++k)

ans = (ans + dp[n][j][k]) % kMod;

return ans;

}

};

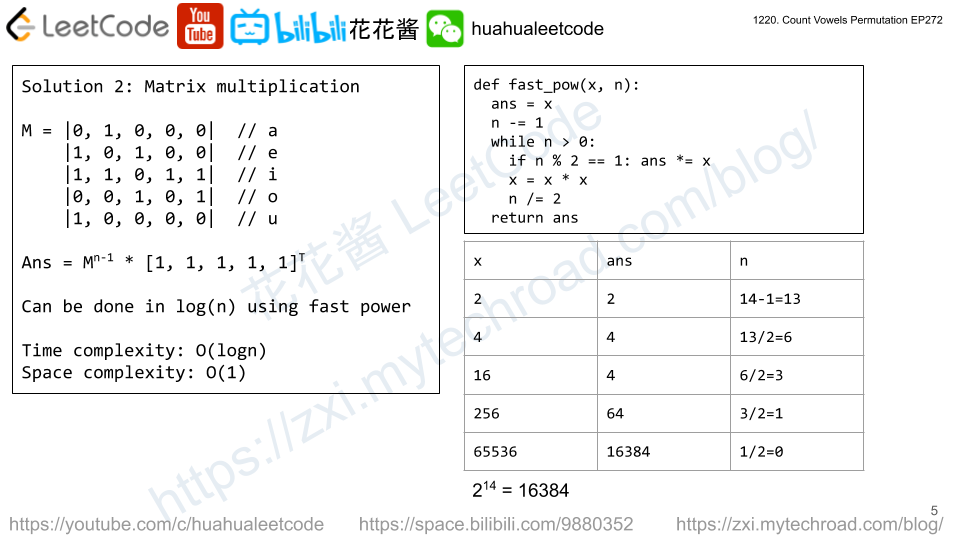
Solution 2: DP with compressed state

dp[i][j] := # of sequences of length i end with j
dp[i][j] := sum(dp[i-1]) – invalid

Time complexity: O(n*6)
Space complexity: O(n*6)

C++

// Author: Huahua

class Solution {

public:

int dieSimulator(int n, vector<int>& rollMax) {

constexpr int kMod = 1e9 + 7;

// dp[i][j] := # of sequences ends with j after i rolls

vector<vector<int>> dp(n + 1, vector<int>(7));

vector<int> sums(n + 1); // sums[i] := sum(dp[i])

for (int j = 0; j < 6; ++j)

sums[1] += dp[1][j] = 1; // 1 roll, 1 dice, 1 way

for (int i = 2; i <= n; ++i)

for (int j = 0; j < 6; ++j) {

const int k = i - rollMax[j];

const int invalid = k <= 1 ? max(k, 0) : sums[k - 1] - dp[k - 1][j];

dp[i][j] = ((sums[i - 1] - invalid) % kMod + kMod) % kMod;

sums[i] = (sums[i] + dp[i][j]) % kMod;

}

return sums[n];

}

};

花花酱 LeetCode 1220. Count Vowels Permutation

By zxi on October 5, 2019

Given an integer n, your task is to count how many strings of length n can be formed under the following rules:

Each character is a lower case vowel ('a', 'e', 'i', 'o', 'u')
Each vowel 'a' may only be followed by an 'e'.
Each vowel 'e' may only be followed by an 'a' or an 'i'.
Each vowel 'i' may not be followed by another 'i'.
Each vowel 'o' may only be followed by an 'i' or a 'u'.
Each vowel 'u' may only be followed by an 'a'.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: n = 1
Output: 5
Explanation: All possible strings are: "a", "e", "i" , "o" and "u".

Example 2:

Input: n = 2
Output: 10
Explanation: All possible strings are: "ae", "ea", "ei", "ia", "ie", "io", "iu", "oi", "ou" and "ua".

Example 3:

Input: n = 5
Output: 68

Constraints:

1 <= n <= 2 * 10^4

Solution: DP

dp[i][c] := number of strings of length i ends with letter c
transition: follow the definition
ans = sum(dp[n])

Time complexity: O(n)
Space complexity: O(n) -> O(1)

C++

// Author: Huahua

class Solution {

public:

int countVowelPermutation(int n) {

constexpr int kMod = 1e9 + 7;

vector<vector<long>> dp(n + 1, vector<long>(5));

fill(begin(dp[1]), end(dp[1]), 1);

// 0: a, 1: e, 2: i, 3: o, 4: u

for (int i = 2; i <= n; ++i) {

dp[i][1] += dp[i - 1][0]; // a -> e

dp[i][0] += dp[i - 1][1]; // e -> a

dp[i][2] += dp[i - 1][1]; // e -> i

for (int j = 0; j < 5; ++j) {

if (j == 2) continue;

dp[i][j] += dp[i - 1][2]; // i -> *

}

dp[i][2] += dp[i - 1][3]; // o -> i

dp[i][4] += dp[i - 1][3]; // o -> u

dp[i][0] += dp[i - 1][4]; // u -> a

for (int j = 0; j < 5; ++j)

dp[i][j] %= kMod;

}

return accumulate(begin(dp[n]), end(dp[n]), 0L) % kMod;

}

};

C++/O(1)

// Author: Huahua

class Solution {

public:

int countVowelPermutation(int n) {

constexpr int kMod = 1e9 + 7;

long a = 1, e = 1, i = 1, o = 1, u = 1;

for (int k = 2; k <= n; ++k) {

long aa = (i + e + u) % kMod;

long ee = (i + a) % kMod;

long ii = (e + o) % kMod;

long oo = i % kMod;

long uu = (i + o) % kMod;

a = aa;

e = ee;

i = ii;

o = oo;

u = uu;

}

return (a + e + i + o + u) % kMod;

}

};

Solution 2: Matrix multiplication

Time complexity: O(logn)
Space complexity: O(1)

C++

// Author: Huahua

constexpr int kMod = 1e9 + 7;

vector<vector<long>> operator*(const vector<vector<long>>& A, const vector<vector<long>>& B) {

int m = A.size();

int x = A[0].size();

int n = B[0].size();

vector<vector<long>> C(m, vector<long>(n));

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j) {

for (int k = 0; k < x; ++k)

C[i][j] += A[i][k] * B[k][j];

C[i][j] %= kMod;

}

return C;

}

class Solution {

public:

int countVowelPermutation(int n) {

vector<vector<long>> m{

{0, 1, 0, 0, 0}, // a

{1, 0, 1, 0, 0}, // e

{1, 1, 0, 1, 1}, // i

{0, 0, 1, 0, 1}, // o

{1, 0, 0, 0, 0} // u

};

vector<vector<long>> ans{{1}, {1}, {1}, {1}, {1}};

n -= 1;

while (n > 0) {

if (n % 2) ans = m * ans;

m = m * m;

n /= 2;

}

long sum = 0;

for (int i = 0; i < 5; ++i)

sum += ans[i][0];

return sum % kMod;

}

};

花花酱 LeetCode 1218. Longest Arithmetic Subsequence of Given Difference

By zxi on October 5, 2019

Given an integer array arr and an integer difference, return the length of the longest subsequence in arr which is an arithmetic sequence such that the difference between adjacent elements in the subsequence equals difference.

Example 1:

Input: arr = [1,2,3,4], difference = 1
Output: 4
Explanation: The longest arithmetic subsequence is [1,2,3,4].

Example 2:

Input: arr = [1,3,5,7], difference = 1
Output: 1
Explanation: The longest arithmetic subsequence is any single element.

Example 3:

Input: arr = [1,5,7,8,5,3,4,2,1], difference = -2
Output: 4
Explanation: The longest arithmetic subsequence is [7,5,3,1].

Constraints:

1 <= arr.length <= 10^5
-10^4 <= arr[i], difference <= 10^4

Solution: DP

dp[i] := max length of sequence ends with x
dp[x] = max(0, dp[x – diff]) + 1

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int longestSubsequence(vector<int>& arr, int d) {

unordered_map<int, int> dp;

int ans = 0;

for (int x : arr)

ans = max(ans, dp[x] = dp[x - d] + 1);

return ans;

}

};

花花酱 LeetCode 89. Gray Code

By zxi on September 29, 2019

The gray code is a binary numeral system where two successive values differ in only one bit.

Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0.

Example 1:

Input: 2
Output: [0,1,3,2]
Explanation:
00 - 0
01 - 1
11 - 3
10 - 2

For a given n, a gray code sequence may not be uniquely defined.
For example, [0,2,3,1] is also a valid gray code sequence.

00 - 0
10 - 2
11 - 3
01 - 1

Example 2:

Input: 0
Output: [0]
Explanation: We define the gray code sequence to begin with 0.
             A gray code sequence of n has size = 2ⁿ, which for n = 0 the size is 2⁰ = 1.
             Therefore, for n = 0 the gray code sequence is [0].

Solution: DP

dp[0] = 0
dp[i] = dp[i – 1] + [x | 1 << (i – 1) for x in reversed(dp[i – 1])]

Time complexity: O(2^n)
Space complexity: O(2^n)

C++

// Author: Huahua

class Solution {

public:

vector<int> grayCode(int n) {

vector<vector<int>> dp(n + 1);

dp[0] = {0};

for (int i = 1; i <= n; ++i) {

dp[i] = dp[i - 1];

for (int j = dp[i - 1].size() - 1; j >= 0; --j)

dp[i].push_back(dp[i - 1][j] | (1 << (i - 1)));

}

return dp[n];

}

};

Python3

# Author: Huahua

class Solution:

def grayCode(self, n: int) -> List[int]:

dp = [0]

for i in range(n):

dp = dp + [x | 1 << i for x in reversed(dp)]

return dp

花花酱 LeetCode 96. Unique Binary Search Trees

By zxi on September 29, 2019

Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?

Example:

Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

Solution: DP

dp[i] = sum(dp[j] * dp[i – j – 1]) (0 <= j < i )

root: 1 node
left child: j nodes
right child i – j – 1 nodes

try all possible partitions

ans = dp[n]

Time complexity: O(n^2)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int numTrees(int n) {

vector<int> dp(n + 1);

dp[0] = 1;

for (int i = 1; i <= n; i++)

for(int j = 0; j < i; j++)

dp[i] += dp[j] * dp[i - j - 1];

return dp[n];

}

};