Problem:
You are given a string expression representing a Lisp-like expression to return the integer value of.
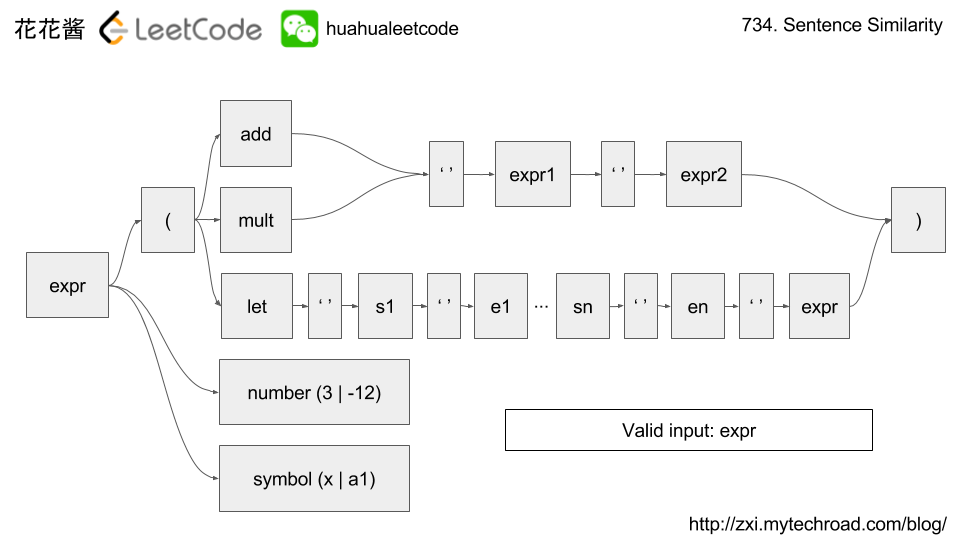
The syntax for these expressions is given as follows.
- An expression is either an integer, a let-expression, an add-expression, a mult-expression, or an assigned variable. Expressions always evaluate to a single integer.
- (An integer could be positive or negative.)
- A let-expression takes the form
(let v1 e1 v2 e2 ... vn en expr), whereletis always the string"let", then there are 1 or more pairs of alternating variables and expressions, meaning that the first variablev1is assigned the value of the expressione1, the second variablev2is assigned the value of the expressione2, and so on sequentially; and then the value of this let-expression is the value of the expressionexpr. - An add-expression takes the form
(add e1 e2)whereaddis always the string"add", there are always two expressionse1, e2, and this expression evaluates to the addition of the evaluation ofe1and the evaluation ofe2. - A mult-expression takes the form
(mult e1 e2)wheremultis always the string"mult", there are always two expressionse1, e2, and this expression evaluates to the multiplication of the evaluation ofe1and the evaluation ofe2. - For the purposes of this question, we will use a smaller subset of variable names. A variable starts with a lowercase letter, then zero or more lowercase letters or digits. Additionally for your convenience, the names “add”, “let”, or “mult” are protected and will never be used as variable names.
- Finally, there is the concept of scope. When an expression of a variable name is evaluated, within the context of that evaluation, the innermost scope (in terms of parentheses) is checked first for the value of that variable, and then outer scopes are checked sequentially. It is guaranteed that every expression is legal. Please see the examples for more details on scope.
Evaluation Examples:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
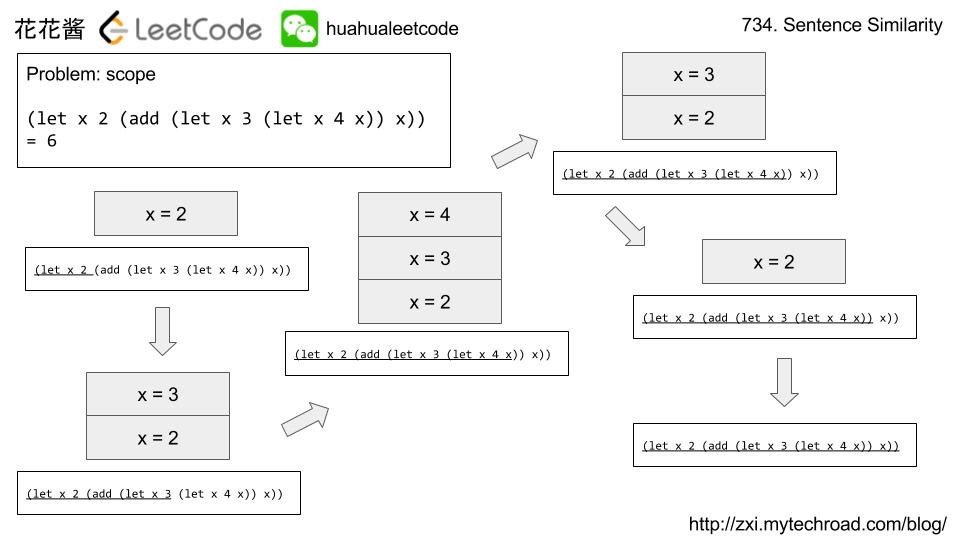
Input: (add 1 2) Output: 3 Input: (mult 3 (add 2 3)) Output: 15 Input: (let x 2 (mult x 5)) Output: 10 Input: (let x 2 (mult x (let x 3 y 4 (add x y)))) Output: 14 Explanation: In the expression (add x y), when checking for the value of the variable x, we check from the innermost scope to the outermost in the context of the variable we are trying to evaluate. Since x = 3 is found first, the value of x is 3. Input: (let x 3 x 2 x) Output: 2 Explanation: Assignment in let statements is processed sequentially. Input: (let x 1 y 2 x (add x y) (add x y)) Output: 5 Explanation: The first (add x y) evaluates as 3, and is assigned to x. The second (add x y) evaluates as 3+2 = 5. Input: (let x 2 (add (let x 3 (let x 4 x)) x)) Output: 6 Explanation: Even though (let x 4 x) has a deeper scope, it is outside the context of the final x in the add-expression. That final x will equal 2. Input: (let a1 3 b2 (add a1 1) b2) Output 4 Explanation: Variable names can contain digits after the first character. |
Note:
- The given string
expressionis well formatted: There are no leading or trailing spaces, there is only a single space separating different components of the string, and no space between adjacent parentheses. The expression is guaranteed to be legal and evaluate to an integer. - The length of
expressionis at most 2000. (It is also non-empty, as that would not be a legal expression.) - The answer and all intermediate calculations of that answer are guaranteed to fit in a 32-bit integer.
Idea:
Recursive parsing
Time complexity: O(n^2) in worst case O(n) in practice
Space complexity: O(n)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
// Author: Huahua // Runtime: 3 ms class Solution { public: int evaluate(string expression) { scopes_.clear(); int pos = 0; return eval(expression, pos); } private: int eval(const string& s, int& pos) { scopes_.push_front(unordered_map<string, int>()); int value = 0; // The return value of current expr if (s[pos] == '(') ++pos; // command, variable or number const string token = getToken(s, pos); if (token == "add") { int v1 = eval(s, ++pos); int v2 = eval(s, ++pos); value = v1 + v2; } else if (token == "mult") { int v1 = eval(s, ++pos); int v2 = eval(s, ++pos); value = v1 * v2; } else if (token == "let") { string var; // expecting " var1 exp1 var2 exp2 ... last_expr)" while (s[pos] != ')') { ++pos; // Must be last_expr if (s[pos] == '(') { value = eval(s, ++pos); break; } // Get a token, could be "x" or "-12" for last_expr var = getToken(s, pos); // End of let, var is last_expr if (s[pos] == ')') { if (isalpha(var[0])) value = getValue(var); else value = stoi(var); break; } // x -12 -> set x to -12 and store in the current scope and take it as the current return value value = scopes_.front()[var] = eval(s, ++pos); } } else if (isalpha(token[0])) { value = getValue(token); // symbol } else { value = std::stoi(token); // number } if (s[pos] == ')') ++pos; scopes_.pop_front(); return value; } int getValue(const string& symbol) { for (const auto& scope : scopes_) if (scope.count(symbol)) return scope.at(symbol); return 0; } // Get a token from current pos. // "let x" -> "let" // "-12 (add x y)" -> "-12" string getToken(const string& s, int& pos) { string token; while (pos < s.length()) { if (s[pos] == ')' || s[pos] == ' ') break; token += s[pos++]; } return token; } deque<unordered_map<string, int>> scopes_; }; |