Posts published in “Simulation”

花花酱 LeetCode 1222. Queens That Can Attack the King

By zxi on October 14, 2019

On an 8×8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

Example 1:

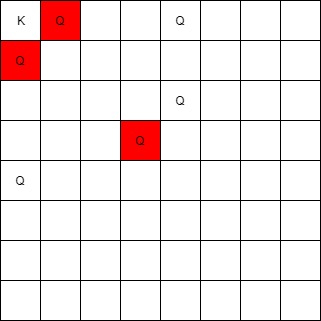
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:  
The queen at [0,1] can attack the king cause they're in the same row. 
The queen at [1,0] can attack the king cause they're in the same column. 
The queen at [3,3] can attack the king cause they're in the same diagnal. 
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:

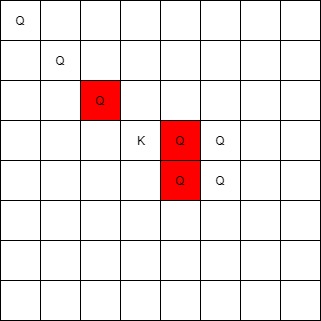
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

Example 3:

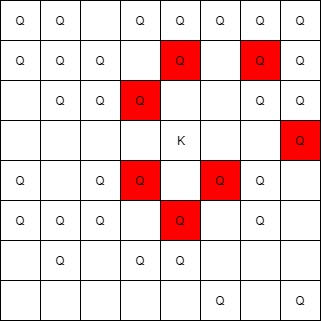
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

Constraints:

1 <= queens.length <= 63
queens[0].length == 2
0 <= queens[i][j] < 8
king.length == 2
0 <= king[0], king[1] < 8
At most one piece is allowed in a cell.

Solution2: Simulation

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {

vector<vector<int>> b(8, vector<int>(8));

for (const auto& q : queens)

b[q[0]][q[1]] = 1;

vector<vector<int>> ans;

for (const auto& q : queens) {

for (int dx = -1; dx <= 1; ++dx)

for (int dy = -1; dy <= 1; ++dy) {

if (dx == 0 && dy == 0) continue;

int x = q[1] + dx;

int y = q[0] + dy;

while (x >= 0 && y >= 0 && x < 8 && y < 8 && !b[y][x]) {

if (x == king[1] && y == king[0])

ans.push_back(q);

x += dx;

y += dy;

}

return ans;

}

};

Solution 2: HashTable + Binary Search

Time complexity: O(nlogn)
Space complexity: O(n)

Support arbitrarily large boards, e.g. 1e9 x 1e9 with 1e6 # of queens.

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) {

unordered_map<int, map<int, vector<int>>> rows, cols, diag1, diag2;

for (const auto& q : queens) {

const int x = q[1];

const int y = q[0];

rows[y][x] = q;

cols[x][y] = q;

diag1[x + y][x] = q;

diag2[x - y][x] = q;

}

const int x = king[1];

const int y = king[0];

vector<vector<int>> ans;

find(rows, y, x, ans);

find(cols, x, y, ans);

find(diag1, x + y, x, ans);

find(diag2, x - y, x, ans);

return ans;

}

private:

void find(const unordered_map<int, map<int, vector<int>>>& m, int idx, int key, vector<vector<int>>& ans) {

if (!m.count(idx)) return;

const auto& d = m.at(idx);

auto it = d.upper_bound(key);

if (it != end(d))

ans.push_back(it->second);

if (it != begin(d))

ans.push_back(prev(it)->second);

}

};

花花酱 LeetCode 1073. Adding Two Negabinary Numbers

By zxi on June 6, 2019

Given two numbers arr1 and arr2 in base -2, return the result of adding them together.

Each number is given in array format: as an array of 0s and 1s, from most significant bit to least significant bit. For example, arr = [1,1,0,1] represents the number (-2)^3 + (-2)^2 + (-2)^0 = -3. A number arr in array format is also guaranteed to have no leading zeros: either arr == [0] or arr[0] == 1.

Return the result of adding arr1 and arr2 in the same format: as an array of 0s and 1s with no leading zeros.

Example 1:

Input: arr1 = [1,1,1,1,1], arr2 = [1,0,1]
Output: [1,0,0,0,0]
Explanation: arr1 represents 11, arr2 represents 5, the output represents 16.

Note:

1 <= arr1.length <= 1000
1 <= arr2.length <= 1000
arr1 and arr2 have no leading zeros
arr1[i] is 0 or 1
arr2[i] is 0 or 1

Solution: Simulation

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua, 8 ms, 9.2 MB

class Solution {

public:

vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {

int i = arr1.size();

int j = arr2.size();

int carry = 0;

vector<int> ans;

while (i || j || carry) {

int sum = (i ? arr1[--i] : 0) + (j ? arr2[--j] : 0) + carry;

ans.push_back(sum & 1);

carry = -(sum >> 1);

}

while (ans.back() == 0 && ans.size() > 1) ans.pop_back();

reverse(begin(ans), end(ans));

return ans;

}

};

花花酱 LeetCode 1041. Robot Bounded In Circle

By zxi on May 14, 2019

On an infinite plane, a robot initially stands at (0, 0) and faces north. The robot can receive one of three instructions:

"G": go straight 1 unit;
"L": turn 90 degrees to the left;
"R": turn 90 degress to the right.

The robot performs the instructions given in order, and repeats them forever.

Return true if and only if there exists a circle in the plane such that the robot never leaves the circle.

Example 1:

Input: "GGLLGG"
Output: true
Explanation: 
The robot moves from (0,0) to (0,2), turns 180 degrees, and then returns to (0,0).
When repeating these instructions, the robot remains in the circle of radius 2 centered at the origin.

Example 2:

Input: "GG"
Output: false
Explanation: 
The robot moves north indefinitely.

Example 3:

Input: "GL"
Output: true
Explanation: 
The robot moves from (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ...

Note:

1 <= instructions.length <= 100
instructions[i] is in {'G', 'L', 'R'}

Solution: Simulation

When instructions end, if the robot is back to (0,0) or is not facing north (which guarantees it will come back to 0, 0 for another 1 or 3 rounds)

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

bool isRobotBounded(string instructions) {

int x = 0;

int y = 0;

int d = 0;

vector<int> dx{0, 1, 0, -1};

vector<int> dy{-1, 0, 1, 0};

for (char c : instructions) {

if (c == 'G') {

x += dx[d];

y += dy[d];

} else {

d = (d + (c == 'L' ? 3 : 1)) % 4;

}

return x == 0 && y == 0 || d;

}

};

花花酱 LeetCode 38. Count and Say

By zxi on April 17, 2019

Problem

https://leetcode.com/problems/count-and-say/

The count-and-say sequence is the sequence of integers with the first five terms as following:

1.     1
2.     11
3.     21
4.     1211
5.     111221

1 is read off as "one 1" or 11.
11 is read off as "two 1s" or 21.
21 is read off as "one 2, then one 1" or 1211.

Given an integer n where 1 ≤ n ≤ 30, generate the n^th term of the count-and-say sequence.

Note: Each term of the sequence of integers will be represented as a string.

Example 1:

Input: 1
Output: "1"

Example 2:

Input: 4
Output: "1211"

Solution: Recursion + Simulation

C++

// Author: Huahua, 4 ms, 8.6 MB

class Solution {

public:

string countAndSay(int n) {

string ans = "1";

for (int i = 1; i < n; ++i)

ans = say(ans);

return ans;

}

private:

string say(const string& n){

string ans;

int s = 0, l = n.length();

for (int e = 1; e <= l; ++e)

if (e == l || n[s] != n[e]) {

int count = e - s;

ans += '0' + count;

ans += n[s];

s = e;

}

return ans;

}

};

花花酱 LeetCode 54. Spiral Matrix

By zxi on April 12, 2019

Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.

Example 1:

Input:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

Input:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Solution: Simulation

Keep track of the current bounds (left, right, top, bottom).

Init: left = 0, right = n – 1, top = 0, bottom = m – 1

Each time we move in one direction and shrink the bounds and turn 90 degrees:
1. go right => –top
2. go down => –right
3. go left => ++bottom
4. go up => ++left

C++

class Solution {

public:

vector<int> spiralOrder(vector<vector<int>>& matrix) {

if (matrix.empty()) return {};

int l = 0;

int t = 0;

int r = matrix[0].size();

int b = matrix.size();

const int total = (r--) * (b--);

int d = 0;

int x = 0;

int y = 0;

vector<int> ans;

while (ans.size() < total - 1) {

if (d == 0) {

while (x < r) ans.push_back(matrix[y][x++]);

++t;

} else if (d == 1) {

while (y < b) ans.push_back(matrix[y++][x]);

--r;

} else if (d == 2) {

while (x > l) ans.push_back(matrix[y][x--]);

--b;

} else if (d == 3) {

while (y > t) ans.push_back(matrix[y--][x]);

++l;

}

d = (d + 1) % 4;

}

if (ans.size() != total) ans.push_back(matrix[y][x]);

return ans;

}

};