花花酱 LeetCode 70. Climbing Stairs

By zxi on August 27, 2018

Problem

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Solution: DP

Time complexity: O(n)

Space complexity: O(n)

C++ O(n)

// Author: Huahua

// Running time: 0 ms

class Solution {

public:

int climbStairs(int n) {

// f[i] = climbStairs(i)

vector<int> f(n + 1, 0);

f[0] = f[1] = 1;

// f[i] = f[i-1] + f[i-2]

for (int i = 2;i <= n; ++i)

f[i] = f[i - 1] + f[i - 2];

return f[n];

}

};

C++ O(1)

// Author: Huahua

// Running time: 0 ms

class Solution {

public:

int climbStairs(int n) {

int two = 1;

int one = 1;

int curr = 1;

// curr = two + one

for (int i = 2; i <= n; ++i) {

curr = two + one;

two = one;

one = curr;

}

return curr;

}

};

花花酱 LeetCode 120. Triangle

By zxi on August 27, 2018

Problem

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:

Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

Solution: DP

Time complexity: O(n^2)

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

// [[2] [[2]

// [3, 4]] [5, 6]

// [6, 5, 7]] [11, 10, 11]

// [4, 1, 8, 3]] [15, 11, 18, 14]]

int minimumTotal(vector<vector<int>>& t) {

int n = t.size();

// t[i][j] := minTotalOf(i,j)

// t[i][j] += min(t[i - 1][j], t[i - 1][j - 1])

for (int i = 0; i < n; ++i)

for (int j = 0; j <= i; ++j) {

if (i == 0 && j == 0) continue;

if (j == 0) t[i][j] += t[i - 1][j];

else if (j == i) t[i][j] += t[i - 1][j - 1];

else t[i][j] += min(t[i - 1][j], t[i - 1][j - 1]);

}

return *std::min_element(begin(t.back()), end(t.back()));

}

};

花花酱 LeetCode 894. All Possible Full Binary Trees

By zxi on August 26, 2018

Problem

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Return a list of all possible full binary trees with N nodes. Each element of the answer is the root node of one possible tree.

Each node of each tree in the answer must have node.val = 0.

You may return the final list of trees in any order.

Example 1:

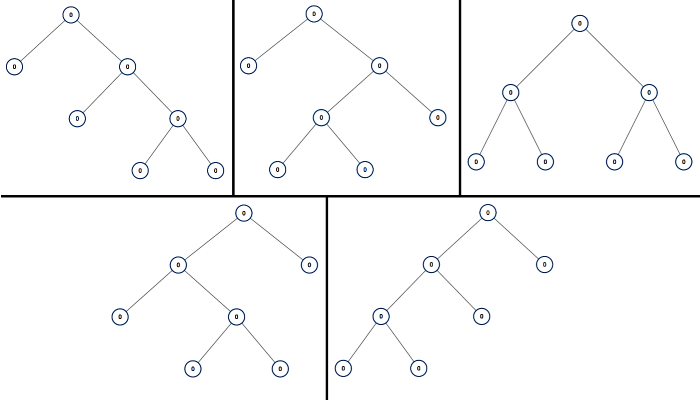
Input: 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Explanation:

Note:

1 <= N <= 20

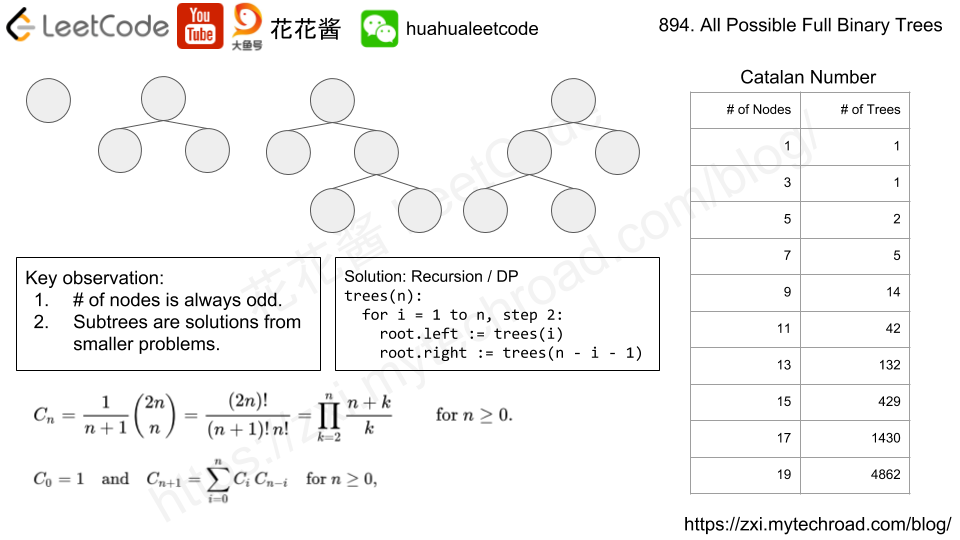
Solution: Recursion

Key observations:

n must be odd, If n is even, no possible trees
ans is the cartesian product of trees(i) and trees(n-i-1). Ans = {Tree(0, l, r) for l, r in trees(i) X trees(N – i – 1)}.

w/o cache

C++

// Author: Huahua

// Running time: 72 ms

class Solution {

public:

vector<TreeNode*> allPossibleFBT(int N) {

if (N % 2 == 0) return {};

if (N == 1) return {new TreeNode(0)};

vector<TreeNode*> ans;

for (int i = 1; i < N; i += 2) {

for (const auto& l : allPossibleFBT(i))

for (const auto& r : allPossibleFBT(N - i - 1)) {

auto root = new TreeNode(0);

root->left = l;

root->right = r;

ans.push_back(root);

}

return ans;

}

};

Java

// Author: Huahua

// Running time: 20 ms

class Solution {

public List<TreeNode> allPossibleFBT(int N) {

List<TreeNode> ans = new ArrayList<>();

if (N % 2 == 0) return ans;

if (N == 1) {

ans.add(new TreeNode(0));

return ans;

}

for (int i = 1; i < N; i += 2) {

for (TreeNode l : allPossibleFBT(i))

for (TreeNode r : allPossibleFBT(N - i - 1)) {

TreeNode root = new TreeNode(0);

root.left = l;

root.right = r;

ans.add(root);

}

return ans;

}

Python

"""

Author: Huahua

Running time: 396 ms

"""

class Solution:

def allPossibleFBT(self, N):

if N % 2 == 0: return []

if N == 1: return [TreeNode(0)]

ans = []

for i in range(1, N, 2):

for l in self.allPossibleFBT(i):

for r in self.allPossibleFBT(N - i - 1):

root = TreeNode(0)

root.left = l

root.right = r

ans.append(root)

return ans

w/cache

C++

// Author: Huahua

// Running time: 68 ms

static constexpr int kMaxN = 20 + 1;

static array<vector<TreeNode*>, kMaxN> m;

class Solution {

public:

vector<TreeNode*> allPossibleFBT(int N) {

return trees(N);

}

private:

vector<TreeNode*>& trees(int N) {

if (m[N].size() > 0) return m[N];

vector<TreeNode*>& ans = m[N];

if (N % 2 == 0) return ans = {};

if (N == 1) ans = {new TreeNode(0)};

for (int i = 1; i < N; i += 2) {

for (const auto& l : trees(i))

for (const auto& r : trees(N - i - 1)) {

auto root = new TreeNode(0);

root->left = l;

root->right = r;

ans.push_back(root);

}

return ans;

}

};

Python

using itertools.product w/ cache

"""

Author: Huahua

Running time: 188 ms

"""

m = [[] for _ in range(21)]

class Solution:

def allPossibleFBT(self, N):

if N % 2 == 0: return []

if N == 1: return [TreeNode(0)]

if len(m[N]) > 0: return m[N]

ans = []

for i in range(1, N, 2):

for l, r in itertools.product(self.allPossibleFBT(i),

self.allPossibleFBT(N - i - 1)):

root = TreeNode(0)

root.left = l

root.right = r

ans.append(root)

m[N] = ans

return ans

C++

// Author: Huahua

// Running time: 100 ms

class Solution {

public:

vector<TreeNode*> allPossibleFBT(int N) {

if (N % 2 == 0) return {};

vector<vector<TreeNode*>> dp(N + 1);

dp[1] = {new TreeNode(0)};

for (int i = 3; i <= N; i += 2)

for (int j = 1; j < i; j += 2) {

int k = i - j - 1;

for (const auto& l : dp[j])

for (const auto& r : dp[k]) {

auto root = new TreeNode(0);

root->left = l;

root->right = r;

dp[i].push_back(root);

}

return dp[N];

}

};

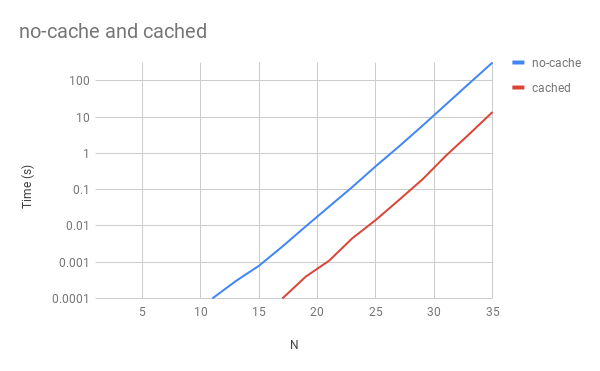
Benchmark

No-cache vs cached

C++

#include <iostream>

#include <vector>

#include <array>

#include <ctime>

#include <cstdio>

using namespace std;

struct TreeNode {

int val;

TreeNode *left;

TreeNode *right;

TreeNode(int x) : val(x), left(NULL), right(NULL) {}

};

static constexpr int kMaxN = 101 + 1;

static array<vector<TreeNode*>, kMaxN> m;

class NoCache {

public:

vector<TreeNode*> allPossibleFBT(int N) {

if (N % 2 == 0) return {};

if (N == 1) return {new TreeNode(0)};

vector<TreeNode*> ans;

for (int i = 1; i < N; i += 2) {

for (const auto& l : allPossibleFBT(i))

for (const auto& r : allPossibleFBT(N - i - 1)) {

auto root = new TreeNode(0);

root->left = l;

root->right = r;

ans.push_back(root);

}

return ans;

}

};

class Cached {

public:

vector<TreeNode*> allPossibleFBT(int N) {

return trees(N);

}

private:

vector<TreeNode*>& trees(int N) {

if (m[N].size() > 0) return m[N];

vector<TreeNode*>& ans = m[N];

if (N % 2 == 0) return ans = {};

if (N == 1) ans = {new TreeNode(0)};

for (int i = 1; i < N; i += 2) {

for (const auto& l : trees(i))

for (const auto& r : trees(N - i - 1)) {

auto root = new TreeNode(0);

root->left = l;

root->right = r;

ans.push_back(root);

}

return ans;

}

};

int main(int argc, char** argv) {

printf("N\tno-cache\tcached\n");

for (int i = 1; i <= 35; i += 2) {

printf("%02d\t", i);

{

auto start = clock();

(void)(NoCache().allPossibleFBT(i));

printf("%8.4f\t", static_cast<double>(clock() - start) / CLOCKS_PER_SEC);

}

{

// Clear the cache.

for (int j = 0; j < kMaxN; ++j)

m[i].clear();

auto start = clock();

(void)(Cached().allPossibleFBT(i));

printf("%8.4f\n", static_cast<double>(clock() - start) / CLOCKS_PER_SEC);

}

return 0;

}

花花酱 LeetCode 303. Range Sum Query – Immutable

By zxi on August 17, 2018

Problem

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

Example:

Given nums = [-2, 0, 3, -5, 2, -1]

sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3

Note:

You may assume that the array does not change.
There are many calls to sumRange function.

Solution: Prefix sum

sums[i] = nums[0] + nums[1] + … + nums[i]

sumRange(i, j) = sums[j] – sums[i – 1]

Time complexity: pre-compute: O(n), query: O(1)

Space complexity: O(n)

// Author: Huahua

// Running time: 112 ms

class NumArray {

public:

NumArray(vector<int> nums): sums_(nums) {

if (nums.empty()) return;

for (int i = 1; i < nums.size();++i)

sums_[i] += sums_[i - 1];

}

int sumRange(int i, int j) {

if (i == 0) return sums_[j];

return sums_[j] - sums_[i-1];

}

private:

vector<int> sums_;

};

花花酱 LeetCode 174. Dungeon Game

By zxi on August 16, 2018

Problem

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).

In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.

For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.

-2 (K)	-3	3
-5	-10	1
10	30	-5 (P)

Note:

The knight’s health has no upper bound.
Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

Solution: DP

Time complexity: O(mn)

Space complexity: O(mn) -> O(n)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int calculateMinimumHP(vector<vector<int>>& dungeon) {

const int m = dungeon.size();

const int n = dungeon[0].size();

// hp[y][x]: min hp required to reach bottom right (P).

vector<vector<int>> hp(m + 1, vector<int>(n + 1, INT_MAX));

hp[m][n - 1] = hp[m - 1][n] = 1;

for (int y = m - 1; y >= 0; --y)

for (int x = n - 1; x >= 0; --x)

hp[y][x] = max(1, min(hp[y + 1][x], hp[y][x + 1]) - dungeon[y][x]);

return hp[0][0];

}

};

O(n) space

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int calculateMinimumHP(vector<vector<int>>& dungeon) {

const int m = dungeon.size();

const int n = dungeon[0].size();

// hp[y][x]: min hp required to reach bottom right (P).

vector<int> hp(n + 1, INT_MAX);

hp[n - 1] = 1;

for (int y = m - 1; y >= 0; --y)

for (int x = n - 1; x >= 0; --x)

hp[x] = max(1, min(hp[x], hp[x + 1]) - dungeon[y][x]);

return hp[0];

}

};

Posts tagged as “dp”

花花酱 LeetCode 70. Climbing Stairs

Problem

Solution: DP

C++ O(n)

C++ O(1)

花花酱 LeetCode 120. Triangle

Problem

Solution: DP

C++

花花酱 LeetCode 894. All Possible Full Binary Trees

Problem

Solution: Recursion

C++

Java

Python

C++

Python

C++

Benchmark

C++

花花酱 LeetCode 303. Range Sum Query – Immutable

Problem

Solution: Prefix sum

花花酱 LeetCode 174. Dungeon Game

Problem

Solution: DP