Posts tagged as “dp”

花花酱 LeetCode 576. Out of Boundary Paths

By zxi on June 2, 2018

Problem

There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 10⁹ + 7.

Example 1:

Input:m = 2, n = 2, N = 2, i = 0, j = 0
Output: 6
Explanation: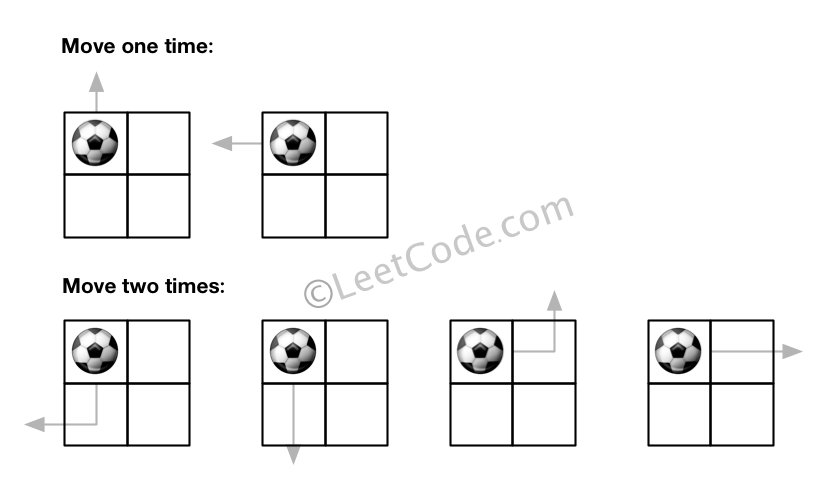

Example 2:

Input:m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
Explanation: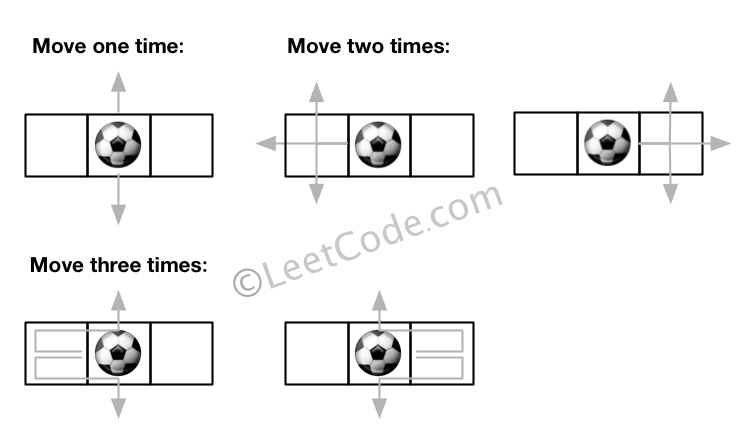

Note:

Once you move the ball out of boundary, you cannot move it back.
The length and height of the grid is in range [1,50].
N is in range [0,50].

Solution

Time complexity: O(m*n + N * m * n)

Space complexity: O(N*m*n) -> O(m*n)

C++

// Author: Huahua

// Running time: 19 ms

class Solution {

public:

int findPaths(int m, int n, int N, int i, int j) {

constexpr int kMod = 1000000007;

vector<vector<vector<int>>> dp(N + 1, vector<vector<int>>(m, vector<int>(n, 0)));

vector<int> dirs{-1, 0, 1, 0, -1};

for (int s = 1; s <= N; ++s)

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

for (int d = 0; d < 4; ++d) {

int tx = x + dirs[d];

int ty = y + dirs[d + 1];

if (tx < 0 || ty < 0 || tx >= n || ty >= m)

dp[s][y][x] += 1;

else

dp[s][y][x] = (dp[s][y][x] + dp[s - 1][ty][tx]) % kMod;

}

return dp[N][i][j];

}

};

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

int findPaths(int m, int n, int N, int i, int j) {

constexpr int kMod = 1000000007;

vector<vector<int>> dp(m, vector<int>(n, 0));

vector<int> dirs{-1, 0, 1, 0, -1};

for (int s = 1; s <= N; ++s) {

vector<vector<int>> tmp(m, vector<int>(n, 0));

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

for (int d = 0; d < 4; ++d) {

int tx = x + dirs[d];

int ty = y + dirs[d + 1];

if (tx < 0 || ty < 0 || tx >= n || ty >= m)

tmp[y][x] += 1;

else

tmp[y][x] = (tmp[y][x] + dp[ty][tx]) % kMod;

}

dp.swap(tmp);

}

return dp[i][j];

}

};

Recursion with memorization

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int findPaths(int m, int n, int N, int i, int j) {

m_ = m;

n_ = n;

dp_ = vector<vector<vector<int>>>(N + 1, vector<vector<int>>(m, vector<int>(n, INT_MIN)));

return paths(N, j, i);

}

private:

vector<vector<vector<int>>> dp_;

int m_;

int n_;

// number of paths starts from out-of-boundary to (x, y) by moving at most N steps.

int paths(int N, int x, int y) {

static vector<int> dirs{-1, 0, 1, 0, -1};

static const int kMod = 1000000007;

// Out of boundary, one path.

if (x < 0 || x >= n_ || y < 0 || y >= m_) return 1;

// Can not move but still in the grid, no path.

if (N == 0) return 0;

// Already computed.

if (dp_[N][y][x] != INT_MIN) return dp_[N][y][x];

dp_[N][y][x] = 0;

for (int d = 0; d < 4; ++d) {

int tx = x + dirs[d];

int ty = y + dirs[d + 1];

dp_[N][y][x] = (dp_[N][y][x] + paths(N - 1, tx, ty)) % kMod;

}

return dp_[N][y][x];

}

};

no loops

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int findPaths(int m, int n, int N, int i, int j) {

m_ = m;

n_ = n;

dp_ = vector<vector<vector<int>>>(N + 1, vector<vector<int>>(m, vector<int>(n, INT_MIN)));

return paths(N, j, i);

}

private:

vector<vector<vector<int>>> dp_;

int m_;

int n_;

// number of paths start from (x, y) and move at most N steps.

int paths(int N, int x, int y) {

static const int kMod = 1000000007;

if (x < 0 || x >= n_ || y < 0 || y >= m_) return 1;

if (N == 0) return 0;

if (dp_[N][y][x] != INT_MIN) return dp_[N][y][x];

long ans = 0;

ans += paths(N - 1, x + 1, y);

ans += paths(N - 1, x - 1, y);

ans += paths(N - 1, x, y + 1);

ans += paths(N - 1, x, y - 1);

ans %= kMod;

return dp_[N][y][x] = ans;

}

};

Problem

题目大意：找出最长回文子序列的长度。

https://leetcode.com/problems/longest-palindromic-subsequence/description/

Given a string s, find the longest palindromic subsequence’s length in s. You may assume that the maximum length of s is 1000.

Example 1:
Input:

"bbbab"

Output:

One possible longest palindromic subsequence is “bbbb”.

Example 2:
Input:

"cbbd"

Output:

One possible longest palindromic subsequence is “bb”.

Solution: DP

Time complexity: O(n^2)

Space complexity: O(n^2)

C++

// Author: Huahua

// Running time: 102 ms

class Solution {

public:

int longestPalindromeSubseq(string s) {

const int n = s.length();

vector<vector<int>> dp(n, vector<int>(n, 0));

for (int l = 1; l <= n; ++l)

for (int i = 0; i <= n - l; ++i) {

int j = i + l - 1;

if (i == j) {

dp[i][j] = 1;

continue;

}

dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

if (s[i] == s[j])

dp[i][j] = dp[i + 1][j - 1] + 2;

}

return dp[0][n - 1];

}

};

Time complexity: O(n^2)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 28 ms

class Solution {

public:

int longestPalindromeSubseq(string s) {

const int n = s.length();

vector<int> dp0(n); // sols of len = l

vector<int> dp1(n); // sols of len = l - 1

vector<int> dp2(n); // sols of len = l - 2

for (int l = 1; l <= n; ++l) {

for (int i = 0; i <= n - l; ++i) {

int j = i + l - 1;

if (i == j) {

dp0[i] = 1;

continue;

}

if (s[i] == s[j])

dp0[i] = dp2[i + 1] + 2;

else

dp0[i] = max(dp1[i + 1], dp1[i]);

}

dp0.swap(dp1);

dp2.swap(dp0);

}

return dp1[0];

}

};

Python3

"""

Author: Huahua

Running time: 1276 ms

"""

class Solution:

def longestPalindromeSubseq(self, s):

n = len(s)

dp0 = [0] * n

dp1 = [1] * n

dp2 = [0] * n

for l in range(2, n + 1):

for i in range(0, n - l + 1):

j = i + l - 1

if s[i] == s[j]:

dp0[i] = dp2[i + 1] + 2

else:

dp0[i] = max(dp1[i + 1], dp1[i])

dp0, dp1, dp2 = dp2, dp0, dp1

return dp1[0]

// Author: Huahua

// Running time: 116 ms (beats 100%)

public class Solution {

public int LongestPalindromeSubseq(string s) {

var n = s.Length;

var dp0 = new int[n];

var dp1 = new int[n];

var dp2 = new int[n];

for (var l = 1; l <= n; ++l) {

for (var i = 0; i <= n - l; ++i) {

int j = i + l - 1;

if (i == j) {

dp0[i] = 1;

continue;

}

if (s[i] == s[j])

dp0[i] = dp2[i + 1] + 2;

else

dp0[i] = Math.Max(dp1[i], dp1[i + 1]);

}

var tmp = dp2;

dp2 = dp1;

dp1 = dp0;

dp0 = tmp;

}

return dp1[0];

}

花花酱 LeetCode 329. Longest Increasing Path in a Matrix

By zxi on May 24, 2018

Problem

Given an integer matrix, find the length of the longest increasing path.

From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).

Example 1:

Input: nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
] 
Output: 4 
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

Input: nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
] 
Output: 4 
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Solution1: DFS + Memorization

Time complexity: O(mn)

Space complexity: O(mn)

C++

// Author: Huahua

// Running time: 36 ms

class Solution {

public:

int longestIncreasingPath(vector<vector<int>>& matrix) {

if (matrix.empty()) return 0;

m_ = matrix.size();

n_ = matrix[0].size();

dp_ = vector<vector<int>>(m_, vector<int>(n_, -1));

int ans = 0;

for (int y = 0; y < m_; ++y)

for (int x = 0; x < n_; ++x)

ans = max(ans, dfs(matrix, x, y));

return ans;

}

private:

int dfs(const vector<vector<int>>& mat, int x, int y) {

if (dp_[y][x] != -1) return dp_[y][x];

static int dirs[] = {0, -1, 0, 1, 0};

dp_[y][x] = 1;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || ty < 0 || tx >= n_ || ty >= m_ || mat[ty][tx] <= mat[y][x])

continue;

dp_[y][x] = max(dp_[y][x], 1 + dfs(mat, tx, ty));

}

return dp_[y][x];

}

int m_;

int n_;

// dp[i][j]: max length start from (j, i)

vector<vector<int>> dp_;

};

Solution2: DP

Time complexity: O(mn*log(mn))

Space complexity: O(mn)

// Author: Huahua

// Running time: 63 ms

class Solution {

public:

int longestIncreasingPath(vector<vector<int>>& matrix) {

if (matrix.empty()) return 0;

int m = matrix.size();

int n = matrix[0].size();

vector<vector<int>> dp(m, vector<int>(n, 1));

int ans = 0;

vector<pair<int, pair<int, int>>> cells;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

cells.push_back({matrix[y][x], {x, y}});

sort(cells.rbegin(), cells.rend());

vector<int> dirs {0, 1, 0, -1, 0};

for (const auto& cell : cells) {

int x = cell.second.first;

int y = cell.second.second;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i];

int ty = y + dirs[i + 1];

if (tx < 0 || tx >= n || ty < 0 || ty >= m) continue;

if (matrix[ty][tx] <= matrix[y][x]) continue;

dp[y][x] = max(dp[y][x], 1 + dp[ty][tx]);

}

ans = max(ans, dp[y][x]);

}

return ans;

}

};

花花酱 LeetCode 826. Most Profit Assigning Work

By zxi on April 29, 2018

Problem

We have jobs: difficulty[i] is the difficulty of the ith job, and profit[i] is the profit of the ith job.

Now we have some workers. worker[i] is the ability of the ith worker, which means that this worker can only complete a job with difficulty at most worker[i].

Every worker can be assigned at most one job, but one job can be completed multiple times.

For example, if 3 people attempt the same job that pays $1, then the total profit will be $3. If a worker cannot complete any job, his profit is $0.

What is the most profit we can make?

Example 1:

Input: difficulty = [2,4,6,8,10], profit = [10,20,30,40,50], worker = [4,5,6,7]
Output: 100 
Explanation: Workers are assigned jobs of difficulty [4,4,6,6] and they get profit of [20,20,30,30] seperately.

Notes:

1 <= difficulty.length = profit.length <= 10000
1 <= worker.length <= 10000
difficulty[i], profit[i], worker[i] are in range [1, 10^5]

Solution 1: Sorting + Two pointers

Time complexity: O(nlogn + mlogm)

Space complexity: O(n)

// Author: Huahua

// Running time: 90 ms

class Solution {

public:

int maxProfitAssignment(vector<int>& difficulty, vector<int>& profit, vector<int>& worker) {

const int n = difficulty.size();

vector<pair<int, int>> jobs; // difficulty, profit

for (int i = 0; i < n; ++i)

jobs.emplace_back(difficulty[i], profit[i]);

std::sort(jobs.begin(), jobs.end());

std::sort(worker.begin(), worker.end());

int ans = 0;

int i = 0;

int best = 0;

for (int level : worker) {

while (i < n && level >= jobs[i].first)

best = max(best, jobs[i++].second);

ans += best;

}

return ans;

}

};

Solution 2: Bucket + Greedy

Key idea: for each difficulty D, find the most profit job whose requirement is <= D.

Three steps:

for each difficulty D, find the most profit job whose requirement is == D, best[D] = max{profit of difficulty D}.
if difficulty D – 1 can make more profit than difficulty D, best[D] = max(best[D], best[D – 1]).
The max profit each worker at skill level D can make is best[D].

Time complexity: O(n)

Space complexity: O(10000)

C++

// Author: Huahua

// Running time: 112 ms

class Solution {

public:

int maxProfitAssignment(vector<int>& difficulty, vector<int>& profit, vector<int>& worker) {

const int N = 100000;

// max profit at difficulty i

vector<int> max_profit(N + 1, 0);

for (int i = 0; i < difficulty.size(); ++i)

max_profit[difficulty[i]] = max(max_profit[difficulty[i]], profit[i]);

for (int i = 2; i <= N; ++i)

max_profit[i] = max(max_profit[i], max_profit[i - 1]);

int ans = 0;

for (int level : worker)

ans += max_profit[level];

return ans;

}

};

C++ using map

// Author: Huahua

// Running time: 112 ms

class Solution {

public:

int maxProfitAssignment(vector<int>& difficulty, vector<int>& profit, vector<int>& worker) {

map<int, int> bests;

for (int i = 0; i < difficulty.size(); ++i)

bests[difficulty[i]] = max(bests[difficulty[i]], profit[i]);

int best = 0;

for (auto it = bests.begin(); it != bests.end(); ++it)

it->second = best = max(it->second, best);

int ans = 0;

for (int level : worker)

ans += prev(bests.upper_bound(level))->second;

return ans;

}

};

花花酱 LeetCode 823. Binary Trees With Factors

By zxi on April 29, 2018

Problem

题目大意：给你一些可以重复使用的数字问能够构成多少种不同的特殊二叉树（根结点的值需为子节点值的乘积）。

https://leetcode.com/problems/binary-trees-with-factors/description/

Given an array of unique integers, each integer is strictly greater than 1.

We make a binary tree using these integers and each number may be used for any number of times.

Each non-leaf node’s value should be equal to the product of the values of it’s children.

How many binary trees can we make? Return the answer modulo 10 ** 9 + 7.

Example 1:

Input: A = [2, 4]
Output: 3 Explanation: We can make these trees: [2], [4], [4, 2, 2]

Example 2:

Input: A = [2, 4, 5, 10]
Output: 7
Explanation: We can make these trees: [2], [4], [5], [10], [4, 2, 2], [10, 2, 5], [10, 5, 2].

Note:

1 <= A.length <= 1000.
2 <= A[i] <= 10 ^ 9.

Solution: DP

Use dp[i] to denote the number of valid binary trees using the first i + 1 smallest elements and roots at A[i].

dp[i] = sum(dp[j] * dp[i/j]), 0 <= j < i, A[i] is a factor of A[j] and A[i] / A[j] also in A.

      A[i]
     /    \
 A[j]  (A[i]/A[j])
  / \     / \
 .....   .....

ans = sum(dp[i]), for all possible i.

Time complexity: O(n^2)

Space complexity: O(n^2)

C++

// Author: Huahua

// Running time: 53 ms

class Solution {

public:

int numFactoredBinaryTrees(vector<int>& A) {

constexpr long kMod = 1000000007;

std::sort(A.begin(), A.end());

unordered_map<int, long> dp;

for (int i = 0; i < A.size(); ++i) {

dp[A[i]] = 1;

for (int j = 0; j < i; ++j)

if (A[i] % A[j] == 0 && dp.count(A[i] / A[j]))

dp[A[i]] += (dp[A[j]] * dp[A[i] / A[j]]) % kMod;

}

long ans = 0;

for (const auto& kv : dp)

ans += kv.second;

return ans % kMod;

}

};

Posts tagged as “dp”

花花酱 LeetCode 576. Out of Boundary Paths

Problem

Solution

Related Problems

花花酱 LeetCode 516. Longest Palindromic Subsequence

Problem

Solution: DP

花花酱 LeetCode 329. Longest Increasing Path in a Matrix

Problem

Solution1: DFS + Memorization

Solution2: DP

花花酱 LeetCode 826. Most Profit Assigning Work

Problem

Solution 1: Sorting + Two pointers

Solution 2: Bucket + Greedy

花花酱 LeetCode 823. Binary Trees With Factors

Problem

Solution: DP