Posts tagged as “dp”

花花酱 LeetCode 799. Champagne Tower

By zxi on March 11, 2018

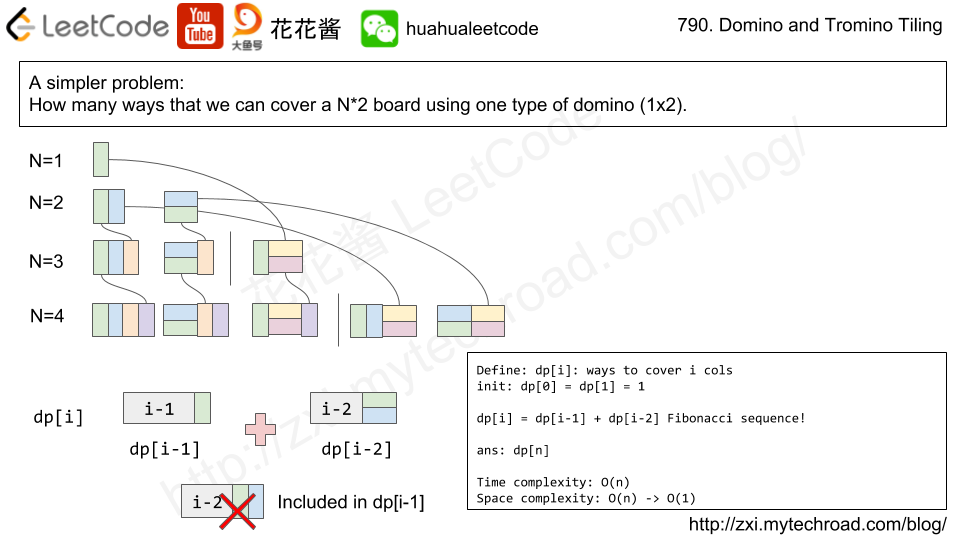
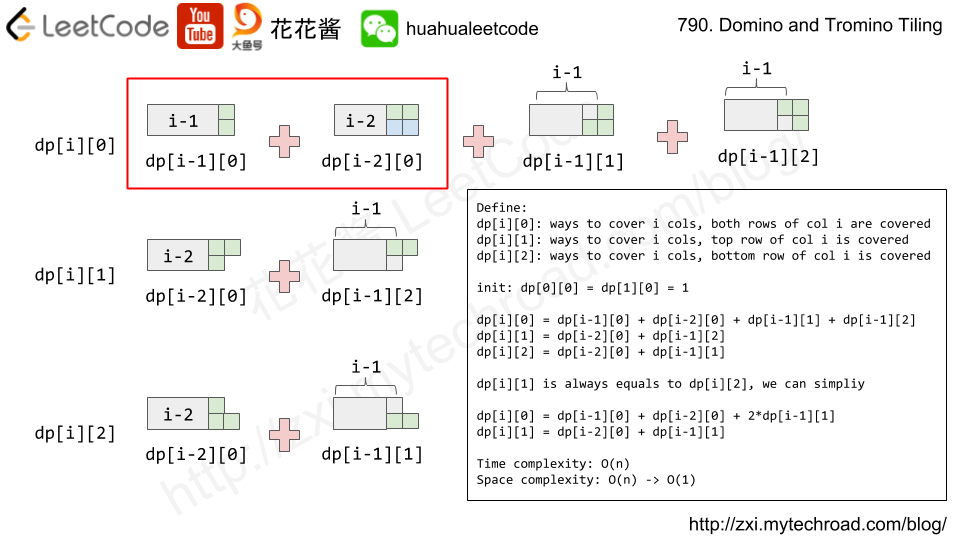
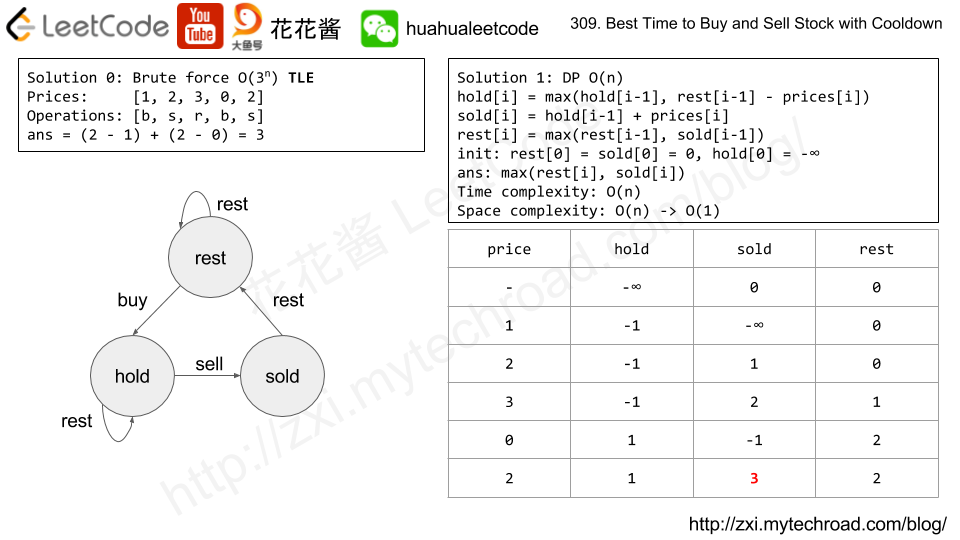
题目大意：往一个香槟塔（i层有i个杯子）倒入n个杯子容量的香槟之后，求指定位置杯子中酒的容量。

Problem:

https://leetcode.com/problems/champagne-tower/description/

We stack glasses in a pyramid, where the first row has 1 glass, the second row has 2 glasses, and so on until the 100th row. Each glass holds one cup (250ml) of champagne.

Then, some champagne is poured in the first glass at the top. When the top most glass is full, any excess liquid poured will fall equally to the glass immediately to the left and right of it. When those glasses become full, any excess champagne will fall equally to the left and right of those glasses, and so on. (A glass at the bottom row has it’s excess champagne fall on the floor.)

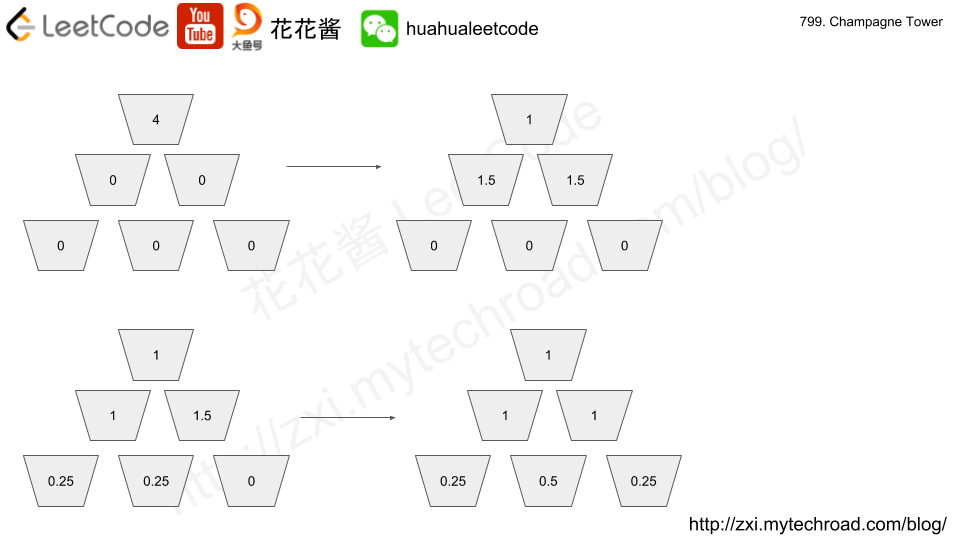
For example, after one cup of champagne is poured, the top most glass is full. After two cups of champagne are poured, the two glasses on the second row are half full. After three cups of champagne are poured, those two cups become full – there are 3 full glasses total now. After four cups of champagne are poured, the third row has the middle glass half full, and the two outside glasses are a quarter full, as pictured below.

Now after pouring some non-negative integer cups of champagne, return how full the j-th glass in the i-th row is (both i and j are 0 indexed.)

Example 1:

Input: poured = 1, query_glass = 1, query_row = 1

Output: 0.0

Explanation: We poured 1 cup of champagne to the top glass of the tower (which is indexed as (0, 0)). There will be no excess liquid so all the glasses under the top glass will remain empty.

Example 2:

Input: poured = 2, query_glass = 1, query_row = 1

Output: 0.5

Explanation: We poured 2 cups of champagne to the top glass of the tower (which is indexed as (0, 0)). There is one cup of excess liquid. The glass indexed as (1, 0) and the glass indexed as (1, 1) will share the excess liquid equally, and each will get half cup of champange.

Note:

poured will be in the range of [0, 10 ^ 9].
query_glass and query_row will be in the range of [0, 99].

Idea: DP + simulation

define dp[i][j] as the volume of champagne will be poured into the j -th glass in the i-th row, dp[i][j] can be greater than 1.

Init dp[0][0] = poured.

Transition: if dp[i][j] > 1, it will overflow, the overflow part will be evenly distributed to dp[i+1][j], dp[i+1][j+1]

if dp[i][j] > 1:
dp[i+1][j] += (dp[i][j] – 1) / 2.0
dp[i+1][j + 1] += (dp[i][j] – 1) / 2.0

Answer: min(1.0, dp[query_row][query_index])

Solution 1:

C++

Time complexity: O(100*100)

Space complexity: O(100*100)

// Author: Huahua

// Running time: 22 ms

class Solution {

public:

double champagneTower(int poured, int query_row, int query_glass) {

constexpr int kRows = 100;

vector<vector<double>> dp(kRows, vector<double>(kRows));

dp[0][0] = poured;

for (int i = 0; i < kRows - 1; ++i)

for (int j = 0; j <= i; ++j)

if (dp[i][j] > 1) {

dp[i + 1][j ] += (dp[i][j] - 1) / 2.0;

dp[i + 1][j + 1] += (dp[i][j] - 1) / 2.0;

dp[i][j] = 1.0;

}

return std::min(1.0, dp[query_row][query_glass]);

}

};

Pull

// Author: Huahua

// Running time: 27 ms

class Solution {

public:

double champagneTower(int poured, int query_row, int query_glass) {

constexpr int kRows = 100;

vector<vector<double>> dp(kRows, vector<double>(kRows));

dp[0][0] = poured;

for (int i = 1; i < kRows; ++i)

for (int j = 0; j <= i; ++j) {

if (j > 0) dp[i][j] += max(0.0, (dp[i - 1][j - 1] - 1) / 2.0);

if (j < i) dp[i][j] += max(0.0, (dp[i - 1][j ] - 1) / 2.0);

}

return std::min(1.0, dp[query_row][query_glass]);

}

};

C++

Time complexity: O(rows * 100)

Space complexity: O(100)

Push

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

double champagneTower(int poured, int query_row, int query_glass) {

constexpr int kCols = 100;

vector<double> dp(kCols);

dp[0] = poured;

for (int i = 0; i < query_row; ++i) {

vector<double> tmp(kCols);

for (int j = 0; j <= i; ++j)

if (dp[j] > 1) {

tmp[j ] += (dp[j] - 1) / 2.0;

tmp[j + 1] += (dp[j] - 1) / 2.0;

}

dp.swap(tmp);

}

return std::min(1.0, dp[query_glass]);

}

};

Pull

class Solution {

public:

double champagneTower(int poured, int query_row, int query_glass) {

constexpr int kCols = 100;

vector<double> dp(kCols);

dp[0] = poured;

for (int i = 1; i <= query_row; ++i) {

vector<double> tmp(kCols);

for (int j = 0; j <= i; ++j) {

if (j > 0) tmp[j] += max(0.0, (dp[j - 1] - 1) / 2.0);

if (j < i) tmp[j] += max(0.0, (dp[j ] - 1) / 2.0);

}

dp.swap(tmp);

}

return std::min(1.0, dp[query_glass]);

}

};

花花酱 LeetCode 518. Coin Change 2

By zxi on March 2, 2018

题目大意：给你一些硬币的面值，问使用这些硬币（无限多块）能够组成amount的方法有多少种。

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.

Note: You can assume that

0 <= amount <= 5000
1 <= coin <= 5000
the number of coins is less than 500
the answer is guaranteed to fit into signed 32-bit integer

Example 1:

Input: amount = 5, coins = [1, 2, 5]

Output: 4

Explanation: there are four ways to make up the amount:

5=5

5=2+2+1

5=2+1+1+1

5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]

Output: 0

Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

1 2	Input: amount = 10, coins = [10] Output: 1

Idea: DP

Transition 1:

Let us use dp[i][j] to denote the number of ways to sum up to amount j using first i kind of coins.

dp[i][j] = dp[i – 1][j – coin] + dp[i – 1][j – 2* coin] + …

Time complexity: O(n*amount^2) TLE

Space complexity: O(n*amount) -> O(amount)

Transition 2:

Let us use dp[i] to denote the number of ways to sum up to amount i.

dp[i + coin] += dp[i]

Time complexity: O(n*amount)

Space complexity: O(amount)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int change(int amount, vector<int>& coins) {

vector<int> dp(amount + 1, 0);

dp[0] = 1;

for (const int coin : coins)

for (int i = 0; i <= amount - coin; ++i)

dp[i + coin] += dp[i];

return dp[amount];

}

};

Java

// Author: Huahua

// Running time: 7 ms

class Solution {

public int change(int amount, int[] coins) {

int[] dp = new int[amount + 1];

dp[0] = 1;

for (int coin : coins)

for (int i = 0; i <= amount - coin; ++i)

dp[i + coin] += dp[i];

return dp[amount];

}

Python

"""

Author: Huahua

Running time: 107 ms (beats 100%)

"""

class Solution(object):

def change(self, amount, coins):

dp = [1] + [0] * (amount);

for coin in coins:

for i in xrange(amount - coin + 1):

if dp[i]:

dp[i + coin] += dp[i]

return dp[amount]

Related Problems:

花花酱 LeetCode 322. Coin Change

花花酱 LeetCode 790. Domino and Tromino Tiling

By zxi on February 24, 2018

题目大意：有两种不同形状的骨牌(1×2长条形，L型）无限多块。给你一个2xN的板子，问一共有多少不同的方式可以完全覆盖。

We have two types of tiles: a 2×1 domino shape, and an “L” tromino shape. These shapes may be rotated.

XX <- domino

XX <- "L" tromino

Given N, how many ways are there to tile a 2 x N board? Return your answer modulo 10^9 + 7.

(In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.)

Example:

Input: 3

Output: 5

Explanation:

The five different ways are listed below, different letters indicates different tiles:

XYZ XXZ XYY XXY XYY

XYZ YYZ XZZ XYY XXY

Idea: DP

dp[i][0]: ways to cover i cols, both rows of i-th col are covered
dp[i][1]: ways to cover i cols, only top row of i-th col is covered
dp[i][2]: ways to cover i cols, only bottom row of i-th col is covered

Solution 1: DP

Time complexity: O(N)

Space complexity: O(N)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numTilings(int N) {

constexpr int kMod = 1000000007;

vector<vector<long>> dp(N + 1, vector<long>(3, 0));

dp[0][0] = dp[1][0] = 1;

for (int i = 2; i <= N; ++i) {

dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + dp[i - 1][1] + dp[i - 1][2]) % kMod;

dp[i][1] = (dp[i - 2][0] + dp[i - 1][2]) % kMod;

dp[i][2] = (dp[i - 2][0] + dp[i - 1][1]) % kMod;

}

return dp[N][0];

}

};

C++ V2

Since dp[i][1] always equals to dp[i][2], we can simplify a bit.

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numTilings(int N) {

constexpr int kMod = 1000000007;

vector<vector<long>> dp(N + 1, vector<long>(2, 0));

dp[0][0] = dp[1][0] = 1;

for (int i = 2; i <= N; ++i) {

dp[i][0] = (dp[i - 1][0] + dp[i - 2][0] + 2 * dp[i - 1][1]) % kMod;

dp[i][1] = (dp[i - 2][0] + dp[i - 1][1]) % kMod;

}

return dp[N][0];

}

};

Solution 2: DP

Another way to think about this problem

define: dp[i] ways to completely covert the i*2 board.

dp[0] = 1 # {}

dp[1] = 1 # {|}

dp[2] = 2 # {||, =}

dp[3] = 5 # {|||, |=, =|, ⌊⌉, ⌈⌋} = dp[2] ⊗ {|} + dp[1] ⊗ {=} + dp[0] ⊗ {⌊⌉, ⌈⌋}

dp[4] = 11 # dp[3] ⊗ {|} + dp[2] ⊗ {=} + dp[1] ⊗ {⌊⌉, ⌈⌋} + dp[0] ⊗ {⌊¯⌋,⌈_⌉}

dp[5] = 24 # dp[4] ⊗ {|} + dp[3] ⊗ {=} + 2*(dp[2] + dp[1] + dp[0])

...

dp[n] = dp[n-1] + dp[n-2] + 2*(dp[n-3] + ... + dp[0])

= dp[n-1] + dp[n-3] + [dp[n-2] + dp[n-3] + 2*(dp[n-4] + ... + dp[0])]

= dp[n-1] + dp[n-3] + dp[n-1]

= 2*dp[n-1] + dp[n-3]

C++

// Author: Huahua

// Running time: 3 ms

class Solution {

public:

int numTilings(int N) {

constexpr int kMod = 1000000007;

vector<long> dp(N + 1, 1);

dp[2] = 2;

for (int i = 3; i <= N; ++i)

dp[i] = (dp[i - 3] + dp[i - 1] * 2) % kMod;

return dp[N];

}

};

花花酱 LeetCode 787. Cheapest Flights Within K Stops

By zxi on February 22, 2018

题目大意：给你一些城市之间的机票价格，问从src到dst的最少需要花多少钱，最多可以中转k个机场。

There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.

Now given all the cities and fights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.

Example 1:

Input:

n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]

src = 0, dst = 2, k = 1

Output: 200

Explanation:

The graph looks like this:

The cheapest price from city <code>0</code> to city <code>2</code> with at most 1 stop costs 200, as marked red in the picture.

Example 2:

Input:

n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]

src = 0, dst = 2, k = 0

Output: 500

Explanation:

The graph looks like this:

The cheapest price from city <code>0</code> to city <code>2</code> with at most 0 stop costs 500, as marked blue in the picture.

Note:

The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
The size of flights will be in range [0, n * (n - 1) / 2].
The format of each flight will be (src, dst, price).
The price of each flight will be in the range [1, 10000].
k is in the range of [0, n - 1].
There will not be any duplicated flights or self cycles.

Solution 1: DFS

w/o prunning TLE

w/ prunning Accepted

C++

// Author: Huahua

// Running time: 36 ms

class Solution {

public:

int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {

g_.clear();

for (const auto& e : flights)

g_[e[0]].emplace_back(e[1], e[2]);

vector<int> visited(n, 0);

visited[src] = 1;

int ans = INT_MAX;

dfs(src, dst, K + 1, 0, visited, ans);

return ans == INT_MAX ? - 1 : ans;

}

private:

unordered_map<int, vector<pair<int,int>>> g_;

void dfs(int src, int dst, int k, int cost, vector<int>& visited, int& ans) {

if (src == dst) {

ans = cost;

return;

}

if (k == 0) return;

for (const auto& p : g_[src]) {

if (visited[p.first]) continue; // do not visit the same city twice.

if (cost + p.second > ans) continue; // IMPORTANT!!! prunning

visited[p.first] = 1;

dfs(p.first, dst, k - 1, cost + p.second, visited, ans);

visited[p.first] = 0;

}

};

Solution 2: BFS

C++

// Author: Huahua

// Running time: 20 ms

class Solution {

public:

int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {

unordered_map<int, vector<pair<int,int>>> g;

for (const auto& e : flights)

g[e[0]].emplace_back(e[1], e[2]);

int ans = INT_MAX;

queue<pair<int,int>> q;

q.push({src, 0});

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

int curr = q.front().first;

int cost = q.front().second;

q.pop();

if (curr == dst)

ans = min(ans, cost);

for (const auto& p : g[curr]) {

if (cost + p.second > ans) continue; // Important: prunning

q.push({p.first, cost + p.second});

}

if (steps++ > K) break;

}

return ans == INT_MAX ? - 1 : ans;

}

};

Solution 3: Bellman-Ford algorithm

dp[k][i]: min cost from src to i taken up to k flights (k-1 stops)

init: dp[0:k+2][src] = 0

transition: dp[k][i] = min(dp[k-1][j] + price[j][i])

ans: dp[K+1][dst]

Time complexity: O(k * |flights|) / O(k*n^2)

Space complexity: O(k*n) -> O(n)

w/o space compression O(k*n)

C++ O(k*n)

// Author: Huahua

// Running time: 15 ms

class Solution {

public:

int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {

constexpr int kInfCost = 1e9;

vector<vector<int>> dp(K + 2, vector<int>(n, kInfCost));

dp[0][src] = 0;

for (int i = 1; i <= K + 1; ++i) {

dp[i][src] = 0;

for (const auto& p : flights)

dp[i][p[1]] = min(dp[i][p[1]], dp[i-1][p[0]] + p[2]);

}

return dp[K + 1][dst] >= kInfCost ? -1 : dp[K + 1][dst];

}

};

C++ O(n)

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {

constexpr int kInfCost = 1e9;

vector<int> cost(n, kInfCost);

cost[src] = 0;

for (int i = 0; i <= K; ++i) {

vector<int> tmp(cost);

for (const auto& p : flights)

tmp[p[1]] = min(tmp[p[1]], cost[p[0]] + p[2]);

cost.swap(tmp);

}

return cost[dst] >= kInfCost ? -1 : cost[dst];

}

};

Java

// Author: Huahua

// Running time: 11 ms

class Solution {

public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {

final int kInfCost = 1<<30;

int[] cost = new int[n];

Arrays.fill(cost, kInfCost);

cost[src] = 0;

for (int i = 0; i <= K; ++i) {

int[] tmp = cost.clone();

for(int[] p: flights)

tmp[p[1]] = Math.min(tmp[p[1]], cost[p[0]] + p[2]);

cost = tmp;

}

return cost[dst] >= kInfCost ? -1 : cost[dst];

}

Python3

"""

Author: Huahua

Running time: 132 ms

"""

class Solution:

def findCheapestPrice(self, n, flights, src, dst, K):

kInfCost = 1e9

cost = [kInfCost for _ in range(n)]

cost[src] = 0

for i in range(K + 1):

tmp = list(cost)

for p in flights:

tmp[p[1]] = min(tmp[p[1]], cost[p[0]] + p[2])

cost = tmp

return -1 if cost[dst] >= 1e9 else cost[dst]

花花酱 LeetCode 309. Best Time to Buy and Sell Stock with Cooldown

By zxi on January 6, 2018

题目大意：给你每天的股价，没有交易次数限制，但是卖出后要休息一天才能再买进。问你最大收益是多少？

Say you have an array for which the i^th element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

prices = [1, 2, 3, 0, 2]

maxProfit = 3

transactions = [buy, sell, cooldown, buy, sell]

Idea:

Solution:

Time complexity: O(n)

Space complexity: O(1)

C++

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

int maxProfit(vector<int>& prices) {

int sold = 0;

int rest = 0;

int hold = INT_MIN;

for (const int price : prices) {

int prev_sold = sold;

sold = hold + price;

hold = max(hold, rest - price);

rest = max(rest, prev_sold);

}

return max(rest, sold);

}

};

Related Problems:

花花酱 LeetCode 121. Best Time to Buy and Sell Stock