Posts tagged as “math”

花花酱 LeetCode 2147. Number of Ways to Divide a Long Corridor

By zxi on February 4, 2022

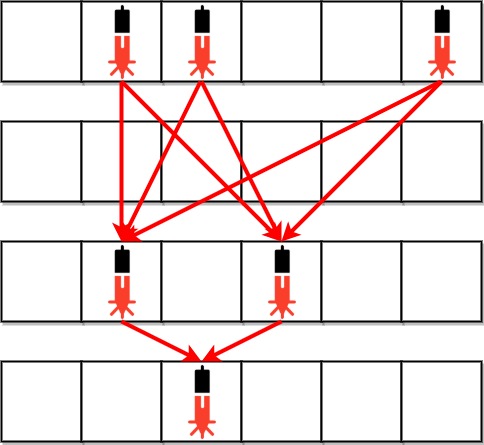
Along a long library corridor, there is a line of seats and decorative plants. You are given a 0-indexed string corridor of length n consisting of letters 'S' and 'P' where each 'S' represents a seat and each 'P' represents a plant.

One room divider has already been installed to the left of index 0, and another to the right of index n - 1. Additional room dividers can be installed. For each position between indices i - 1 and i (1 <= i <= n - 1), at most one divider can be installed.

Divide the corridor into non-overlapping sections, where each section has exactly two seats with any number of plants. There may be multiple ways to perform the division. Two ways are different if there is a position with a room divider installed in the first way but not in the second way.

Return the number of ways to divide the corridor. Since the answer may be very large, return it modulo 10⁹ + 7. If there is no way, return 0.

Example 1:

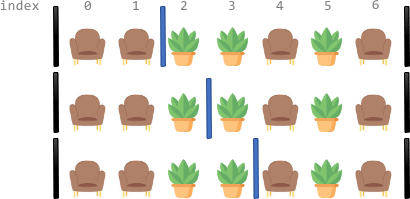
Input: corridor = "SSPPSPS"
Output: 3
Explanation: There are 3 different ways to divide the corridor.
The black bars in the above image indicate the two room dividers already installed.
Note that in each of the ways, each section has exactly two seats.

Example 2:

Input: corridor = "PPSPSP"
Output: 1
Explanation: There is only 1 way to divide the corridor, by not installing any additional dividers.
Installing any would create some section that does not have exactly two seats.

Example 3:

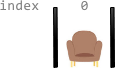
Input: corridor = "S"
Output: 0
Explanation: There is no way to divide the corridor because there will always be a section that does not have exactly two seats.

Constraints:

n == corridor.length
1 <= n <= 10⁵
corridor[i] is either 'S' or 'P'.

Solution: Combination

If the 2k-th seat is positioned at j, and the 2k+1-th seat is at i. There are (i – j) ways to split between these two groups.

ans = prod{i_k – j_k}

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int numberOfWays(string corridor) {

constexpr int kMod = 1e9 + 7;

long ans = 1;

long k = 0;

for (long i = 0, j = 0; i < corridor.size(); ++i) {

if (corridor[i] != 'S') continue;

if (++k > 2 && k & 1)

ans = ans * (i - j) % kMod;

j = i;

}

return (k >= 2 && k % 2 == 0) ? ans : 0;

}

};

花花酱 LeetCode 2145. Count the Hidden Sequences

By zxi on January 31, 2022

You are given a 0-indexed array of n integers differences, which describes the differences between each pair of consecutive integers of a hidden sequence of length (n + 1). More formally, call the hidden sequence hidden, then we have that differences[i] = hidden[i + 1] - hidden[i].

You are further given two integers lower and upper that describe the inclusive range of values [lower, upper] that the hidden sequence can contain.

For example, given differences = [1, -3, 4], lower = 1, upper = 6, the hidden sequence is a sequence of length 4 whose elements are in between 1 and 6 (inclusive).
- [3, 4, 1, 5] and [4, 5, 2, 6] are possible hidden sequences.
- [5, 6, 3, 7] is not possible since it contains an element greater than 6.
- [1, 2, 3, 4] is not possible since the differences are not correct.

Return the number of possible hidden sequences there are. If there are no possible sequences, return 0.

Example 1:

Input: differences = [1,-3,4], lower = 1, upper = 6
Output: 2
Explanation: The possible hidden sequences are:
- [3, 4, 1, 5]
- [4, 5, 2, 6]
Thus, we return 2.

Example 2:

Input: differences = [3,-4,5,1,-2], lower = -4, upper = 5
Output: 4
Explanation: The possible hidden sequences are:
- [-3, 0, -4, 1, 2, 0]
- [-2, 1, -3, 2, 3, 1]
- [-1, 2, -2, 3, 4, 2]
- [0, 3, -1, 4, 5, 3]
Thus, we return 4.

Example 3:

Input: differences = [4,-7,2], lower = 3, upper = 6
Output: 0
Explanation: There are no possible hidden sequences. Thus, we return 0.

Constraints:

n == differences.length
1 <= n <= 10⁵
-10⁵ <= differences[i] <= 10⁵
-10⁵ <= lower <= upper <= 10⁵

Solution: Math

Find the min and max of the cumulative sum of the differences.

Ans = max(0, upper – lower – (hi – lo) + 1)

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int numberOfArrays(vector<int>& differences, int lower, int upper) {

long long s = 0;

long long hi = 0;

long long lo = 0;

for (int d : differences) {

s += d;

hi = max(hi, s);

lo = min(lo, s);

}

return max(0LL, upper - lower - (hi - lo) + 1);

}

};

花花酱 LeetCode 2139. Minimum Moves to Reach Target Score

By zxi on January 30, 2022

You are playing a game with integers. You start with the integer 1 and you want to reach the integer target.

In one move, you can either:

Increment the current integer by one (i.e., x = x + 1).
Double the current integer (i.e., x = 2 * x).

You can use the increment operation any number of times, however, you can only use the double operation at most maxDoubles times.

Given the two integers target and maxDoubles, return the minimum number of moves needed to reach target starting with 1.

Example 1:

Input: target = 5, maxDoubles = 0
Output: 4
Explanation: Keep incrementing by 1 until you reach target.

Example 2:

Input: target = 19, maxDoubles = 2
Output: 7
Explanation: Initially, x = 1
Increment 3 times so x = 4
Double once so x = 8
Increment once so x = 9
Double again so x = 18
Increment once so x = 19

Example 3:

Input: target = 10, maxDoubles = 4
Output: 4
Explanation:Initially, x = 1
Increment once so x = 2
Double once so x = 4
Increment once so x = 5
Double again so x = 10

Constraints:

1 <= target <= 10⁹
0 <= maxDoubles <= 100

Solution: Reverse + Greedy

If num is odd, decrement it by 1. Divide num by 2 until maxdoubles times. Apply decrementing until 1 reached.

ex1: 19 (dec)-> 18 (div1)-> 9 (dec) -> 8 (div2)-> 4 (dec)-> 3 (dec)-> 2 (dec)-> 1

Time complexity: O(logn)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minMoves(int target, int maxDoubles) {

int ans = 0;

while (maxDoubles-- && target != 1) {

if (target & 1)

--target, ++ans;

++ans;

target >>= 1;

}

ans += (target - 1);

return ans;

}

};

花花酱 LeetCode 2125. Number of Laser Beams in a Bank

By zxi on January 2, 2022

Anti-theft security devices are activated inside a bank. You are given a 0-indexed binary string array bank representing the floor plan of the bank, which is an m x n 2D matrix. bank[i] represents the i^th row, consisting of '0's and '1's. '0' means the cell is empty, while'1' means the cell has a security device.

There is one laser beam between any two security devices if both conditions are met:

The two devices are located on two different rows: r₁ and r₂, where r₁ < r₂.
For each row i where r₁ < i < r₂, there are no security devices in the i^th row.

Laser beams are independent, i.e., one beam does not interfere nor join with another.

Return the total number of laser beams in the bank.

Example 1:

Input: bank = ["011001","000000","010100","001000"]
Output: 8
Explanation: Between each of the following device pairs, there is one beam. In total, there are 8 beams:
 * bank[0][1] -- bank[2][1]
 * bank[0][1] -- bank[2][3]
 * bank[0][2] -- bank[2][1]
 * bank[0][2] -- bank[2][3]
 * bank[0][5] -- bank[2][1]
 * bank[0][5] -- bank[2][3]
 * bank[2][1] -- bank[3][2]
 * bank[2][3] -- bank[3][2]
Note that there is no beam between any device on the 0^th row with any on the 3^rd row.
This is because the 2^nd row contains security devices, which breaks the second condition.

Example 2:

Input: bank = ["000","111","000"]
Output: 0
Explanation: There does not exist two devices located on two different rows.

Constraints:

m == bank.length
n == bank[i].length
1 <= m, n <= 500
bank[i][j] is either '0' or '1'.

Solution: Rule of product

Just need to remember the # of devices of prev non-empty row.
# of beams between two non-empty row equals to row[i] * row[j]
ans += prev * curr

Time complexity: O(m*n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int numberOfBeams(vector<string>& bank) {

int ans = 0;

int prev = 0;

for (const string& row : bank)

if (int curr = count(begin(row), end(row), '1')) {

ans += prev * curr;

prev = curr;

}

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def numberOfBeams(self, bank: List[str]) -> int:

ans = prev = 0

for row in bank:

if curr := row.count('1'):

ans += prev * curr

prev = curr

return ans

花花酱 LeetCode 1998. GCD Sort of an Array

By zxi on December 31, 2021

You are given an integer array nums, and you can perform the following operation any number of times on nums:

Swap the positions of two elements nums[i] and nums[j] if gcd(nums[i], nums[j]) > 1 where gcd(nums[i], nums[j]) is the greatest common divisor of nums[i] and nums[j].

Return true if it is possible to sort nums in non-decreasing order using the above swap method, or false otherwise.

Example 1:

Input: nums = [7,21,3]
Output: true
Explanation: We can sort [7,21,3] by performing the following operations:
- Swap 7 and 21 because gcd(7,21) = 7. nums = [21,7,3]
- Swap 21 and 3 because gcd(21,3) = 3. nums = [3,7,21]

Example 2:

Input: nums = [5,2,6,2]
Output: false
Explanation: It is impossible to sort the array because 5 cannot be swapped with any other element.

Example 3:

Input: nums = [10,5,9,3,15]
Output: true
We can sort [10,5,9,3,15] by performing the following operations:
- Swap 10 and 15 because gcd(10,15) = 5. nums = [15,5,9,3,10]
- Swap 15 and 3 because gcd(15,3) = 3. nums = [3,5,9,15,10]
- Swap 10 and 15 because gcd(10,15) = 5. nums = [3,5,9,10,15]

Constraints:

1 <= nums.length <= 3 * 10⁴
2 <= nums[i] <= 10⁵

Solution: Union-Find

Let nums[j]’s target position be i. In order to put nums[j] to pos i by swapping. nums[i] and nums[j] must be in the same connected component. There is an edge between two numbers if they have gcd > 1.

We union two numbers if their have gcd > 1. However, it will be TLE if we do all pairs . Thus, for each number, we union it with its divisors instead.

Time complexity: O(n²) TLE -> O(sum(sqrt(nums[i]))) <= O(n*sqrt(m))
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

bool gcdSort(vector<int>& nums) {

const int m = *max_element(begin(nums), end(nums));

const int n = nums.size();

vector<int> p(m + 1);

iota(begin(p), end(p), 0);

function<int(int)> find = [&](int x) {

return p[x] == x ? x : (p[x] = find(p[x]));

};

for (int x : nums)

for (int d = 2; d <= sqrt(x); ++d)

if (x % d == 0)

p[find(x)] = p[find(x / d)] = find(d);

vector<int> sorted(nums);

sort(begin(sorted), end(sorted));

for (int i = 0; i < n; ++i)

if (find(sorted[i]) != find(nums[i]))

return false;

return true;

}

};