花花酱 LeetCode 480. Sliding Window Median

By zxi on January 28, 2018

题目大意：让你求移动窗口的中位数。

Problem:

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Examples:

[2,3,4] , the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Your job is to output the median array for each window in the original array.

For example,
Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.

Window position Median

--------------- -----

[1 3 -1] -3 5 3 6 7 1

1 [3 -1 -3] 5 3 6 7 -1

1 3 [-1 -3 5] 3 6 7 -1

1 3 -1 [-3 5 3] 6 7 3

1 3 -1 -3 [5 3 6] 7 5

1 3 -1 -3 5 [3 6 7] 6

Therefore, return the median sliding window as [1,-1,-1,3,5,6].

Note:
You may assume k is always valid, ie: k is always smaller than input array’s size for non-empty array.

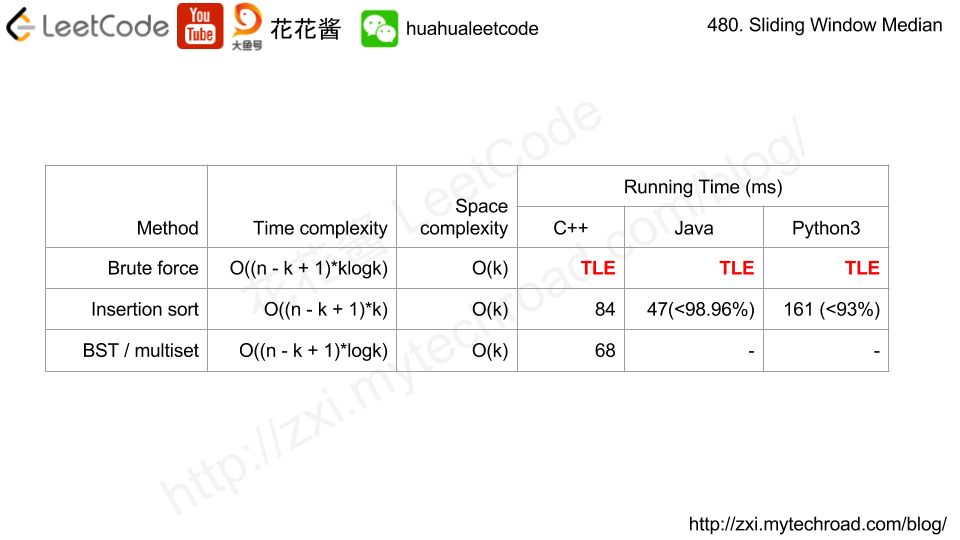
Solution 0: Brute Force

Time complexity: O(n*klogk) TLE 32/42 test cases passed

Solution 1: Insertion Sort

Time complexity: O(k*logk + (n – k + 1)*k)

Space complexity: O(k)

C++ / vector

// Author: Huahua

// Running time: 99 ms

class Solution {

public:

vector<double> medianSlidingWindow(vector<int>& nums, int k) {

vector<double> ans;

if (k == 0) return ans;

vector<int> window(nums.begin(), nums.begin() + k - 1);

std::sort(window.begin(), window.end());

for (int i = k - 1; i < nums.size(); ++i) {

window.push_back(nums[i]);

auto it = prev(window.end(), 1);

auto const insertion_point =

std::upper_bound(window.begin(), it, *it);

std::rotate(insertion_point, it, it + 1);

ans.push_back((static_cast<double>(window[k / 2]) + window[(k - 1) / 2]) / 2);

window.erase(std::find(window.begin(), window.end(), nums[i - k + 1]));

}

return ans;

}

};

C++ / vector + binary_search for deletion.

// Author: Huahua

// Running time: 84 ms

class Solution {

public:

vector<double> medianSlidingWindow(vector<int>& nums, int k) {

vector<double> ans;

if (k == 0) return ans;

vector<int> window(nums.begin(), nums.begin() + k - 1);

std::sort(window.begin(), window.end());

for (int i = k - 1; i < nums.size(); ++i) {

window.push_back(nums[i]);

auto it = prev(window.end(), 1);

auto const insertion_point =

std::upper_bound(window.begin(), it, *it);

std::rotate(insertion_point, it, it + 1);

ans.push_back((static_cast<double>(window[k / 2]) + window[(k - 1) / 2]) / 2);

window.erase(std::lower_bound(window.begin(), window.end(), nums[i - k + 1]));

}

return ans;

}

};

Java

// Author: Huahua

// Running time: 60 ms

class Solution {

public double[] medianSlidingWindow(int[] nums, int k) {

if (k == 0) return new double[0];

double[] ans = new double[nums.length - k + 1];

int[] window = new int[k];

for (int i = 0; i < k; ++i)

window[i] = nums[i];

Arrays.sort(window);

for (int i = k; i <= nums.length; ++i) {

ans[i - k] = ((double)window[k / 2] + window[(k - 1)/2]) / 2;

if (i == nums.length) break;

remove(window, nums[i - k]);

insert(window, nums[i]);

}

return ans;

}

// Insert val into window, window[k - 1] is empty before inseration

private void insert(int[] window, int val) {

int i = 0;

while (i < window.length - 1 && val > window[i]) ++i;

int j = window.length - 1;

while (j > i) window[j] = window[--j];

window[j] = val;

}

// Remove val from window and shrink it.

private void remove(int[] window, int val) {

int i = 0;

while (i < window.length && val != window[i]) ++i;

while (i < window.length - 1) window[i] = window[++i];

}

Java / Binary Search

// Author: Huahua

// Running time: 47 ms (<98.96%)

class Solution {

public double[] medianSlidingWindow(int[] nums, int k) {

if (k == 0) return new double[0];

double[] ans = new double[nums.length - k + 1];

int[] window = new int[k];

for (int i = 0; i < k; ++i)

window[i] = nums[i];

Arrays.sort(window);

for (int i = k; i <= nums.length; ++i) {

ans[i - k] = ((double)window[k / 2] + window[(k - 1)/2]) / 2;

if (i == nums.length) break;

remove(window, nums[i - k]);

insert(window, nums[i]);

}

return ans;

}

// Insert val into window, window[k - 1] is empty before inseration

private void insert(int[] window, int val) {

int i = Arrays.binarySearch(window, val);

if (i < 0) i = - i - 1;

int j = window.length - 1;

while (j > i) window[j] = window[--j];

window[j] = val;

}

// Remove val from window and shrink it.

private void remove(int[] window, int val) {

int i = Arrays.binarySearch(window, val);

while (i < window.length - 1) window[i] = window[++i];

}

Python

"""

Author: Huahua

Running time: 161 ms (< 93.75%)

"""

class Solution:

def medianSlidingWindow(self, nums, k):

if k == 0: return []

ans = []

window = sorted(nums[0:k])

for i in range(k, len(nums) + 1):

ans.append((window[k // 2] + window[(k - 1) // 2]) / 2.0)

if i == len(nums): break

index = bisect.bisect_left(window, nums[i - k])

window.pop(index)

bisect.insort_left(window, nums[i])

return ans

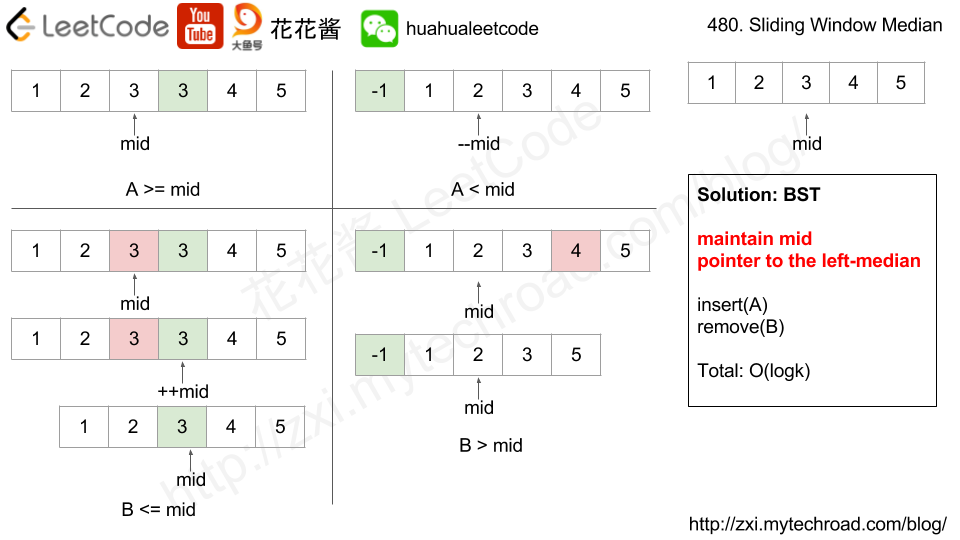
Solution 2: BST

// Author: Huahua

// Running time: 68 ms

class Solution {

public:

vector<double> medianSlidingWindow(vector<int>& nums, int k) {

vector<double> ans;

if (k == 0) return ans;

multiset<int> window(nums.begin(), nums.begin() + k);

auto mid = next(window.begin(), (k - 1) / 2);

for (int i = k; i <= nums.size(); ++i) {

ans.push_back((static_cast<double>(*mid) +

*next(mid, (k + 1) % 2)) / 2.0);

if (i == nums.size()) break;

window.insert(nums[i]);

if (nums[i] < *mid) --mid;

if (nums[i - k] <= *mid) ++mid;

window.erase(window.lower_bound(nums[i - k]));

}

return ans;

}

};

Related Problems:

花花酱 LeetCode 4. Median of Two Sorted Arrays

By zxi on November 8, 2017

题目大意：求两个已经排序的数组的中位数（如果合并后）。

Problem:

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

Example 1:

nums1 = [1, 3]

nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]

nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

Idea:

Binary Search

Time complexity: O(log(min(n1,n2)))

Space complexity: O(1)

Solution: Binary Search

C++

// Author: Huahua

// Runtime: 52 ms

class Solution {

public:

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {

const int n1 = nums1.size();

const int n2 = nums2.size();

// Make sure n1 <= n2

if (n1 > n2) return findMedianSortedArrays(nums2, nums1);

const int k = (n1 + n2 + 1) / 2;

int l = 0;

int r = n1;

while (l < r) {

const int m1 = l + (r - l) / 2;

const int m2 = k - m1;

if (nums1[m1] < nums2[m2 - 1])

l = m1 + 1;

else

r = m1;

}

const int m1 = l;

const int m2 = k - l;

const int c1 = max(m1 <= 0 ? INT_MIN : nums1[m1 - 1],

m2 <= 0 ? INT_MIN : nums2[m2 - 1]);

if ((n1 + n2) % 2 == 1)

return c1;

const int c2 = min(m1 >= n1 ? INT_MAX : nums1[m1],

m2 >= n2 ? INT_MAX : nums2[m2]);

return (c1 + c2) * 0.5;

}

};

Java

// Author: Huahua

// Runtime: 66 ms

class Solution {

public double findMedianSortedArrays(int[] nums1, int[] nums2) {

int n1 = nums1.length;

int n2 = nums2.length;

if (n1 > n2)

return findMedianSortedArrays(nums2, nums1);

int k = (n1 + n2 + 1) / 2;

int l = 0;

int r = n1;

while (l < r) {

int m1 = l + (r - l) / 2;

int m2 = k - m1;

if (nums1[m1] < nums2[m2 - 1])

l = m1 + 1;

else

r = m1;

}

int m1 = l;

int m2 = k - l;

int c1 = Math.max(m1 <= 0 ? Integer.MIN_VALUE : nums1[m1 - 1],

m2 <= 0 ? Integer.MIN_VALUE : nums2[m2 - 1]);

if ((n1 + n2) % 2 == 1)

return c1;

int c2 = Math.min(m1 >= n1 ? Integer.MAX_VALUE : nums1[m1],

m2 >= n2 ? Integer.MAX_VALUE : nums2[m2]);

return (c1 + c2) * 0.5;

}

Posts tagged as “median”

花花酱 LeetCode 480. Sliding Window Median

花花酱 LeetCode 4. Median of Two Sorted Arrays

Solution: Binary Search

C++

Java

Related Problem:

花花酱 LeetCode 295. Find Median from Data Stream O(logn) + O(1)

[ZOJ] 3612: Median