求合取余即可，余数就是答案。
Time complexity: O(n)
Space complexity: O(1)
|
1 2 3 4 5 6 |
class Solution { public: int minOperations(vector<int>& nums, int k) { return accumulate(begin(nums), end(nums), 0) % k; } }; |
Posts tagged as “mod”
Given a positive integer n, find the sum of all integers in the range [1, n] inclusive that are divisible by 3, 5, or 7.
Return an integer denoting the sum of all numbers in the given range satisfying the constraint.
Example 1:
Input: n = 7 Output: 21 Explanation: Numbers in the range[1, 7]that are divisible by3,5,or7are3, 5, 6, 7. The sum of these numbers is21.
Example 2:
Input: n = 10 Output: 40 Explanation: Numbers in the range[1, 10] that aredivisible by3,5,or7are3, 5, 6, 7, 9, 10. The sum of these numbers is 40.
Example 3:
Input: n = 9 Output: 30 Explanation: Numbers in the range[1, 9]that are divisible by3,5, or7are3, 5, 6, 7, 9. The sum of these numbers is30.
Constraints:
1 <= n <= 103
Solution: Mod
Time complexity: O(n)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 |
// Author: Huahua class Solution { public: int sumOfMultiples(int n) { int ans = 0; for (int i = 1; i <= n; ++i) { if (i % 3 == 0 || i % 5 == 0 || i % 7 == 0) ans += i; } return ans; } }; |
There are n people standing in a line labeled from 1 to n. The first person in the line is holding a pillow initially. Every second, the person holding the pillow passes it to the next person standing in the line. Once the pillow reaches the end of the line, the direction changes, and people continue passing the pillow in the opposite direction.
- For example, once the pillow reaches the
nthperson they pass it to then - 1thperson, then to then - 2thperson and so on.
Given the two positive integers n and time, return the index of the person holding the pillow after time seconds.
Example 1:
Input: n = 4, time = 5 Output: 2 Explanation: People pass the pillow in the following way: 1 -> 2 -> 3 -> 4 -> 3 -> 2. Afer five seconds, the pillow is given to the 2nd person.
Example 2:
Input: n = 3, time = 2 Output: 3 Explanation: People pass the pillow in the following way: 1 -> 2 -> 3. Afer two seconds, the pillow is given to the 3rd person.
Constraints:
2 <= n <= 10001 <= time <= 1000
Solution: Math
It takes n – 1 seconds from 1 to n and takes another n – 1 seconds back from n to 1.
So one around takes 2 * (n – 1) seconds. We can mod time with 2 * (n – 1).
After that if time < n – 1 answer is time + 1, otherwise answer is n – (time – (n – 1))
Time complexity: O(1)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 |
// Author: Huahua class Solution { public: int passThePillow(int n, int time) { time %= (2 * (n - 1)); return time > n - 1 ? n - (time - (n - 1)) : time + 1; } }; |
There are n students in a class numbered from 0 to n - 1. The teacher will give each student a problem starting with the student number 0, then the student number 1, and so on until the teacher reaches the student number n - 1. After that, the teacher will restart the process, starting with the student number 0 again.
You are given a 0-indexed integer array chalk and an integer k. There are initially k pieces of chalk. When the student number i is given a problem to solve, they will use chalk[i] pieces of chalk to solve that problem. However, if the current number of chalk pieces is strictly less than chalk[i], then the student number i will be asked to replace the chalk.
Return the index of the student that will replace the chalk.
Example 1:
Input: chalk = [5,1,5], k = 22 Output: 0 Explanation: The students go in turns as follows: - Student number 0 uses 5 chalk, so k = 17. - Student number 1 uses 1 chalk, so k = 16. - Student number 2 uses 5 chalk, so k = 11. - Student number 0 uses 5 chalk, so k = 6. - Student number 1 uses 1 chalk, so k = 5. - Student number 2 uses 5 chalk, so k = 0. Student number 0 does not have enough chalk, so they will have to replace it.
Example 2:
Input: chalk = [3,4,1,2], k = 25 Output: 1 Explanation: The students go in turns as follows: - Student number 0 uses 3 chalk so k = 22. - Student number 1 uses 4 chalk so k = 18. - Student number 2 uses 1 chalk so k = 17. - Student number 3 uses 2 chalk so k = 15. - Student number 0 uses 3 chalk so k = 12. - Student number 1 uses 4 chalk so k = 8. - Student number 2 uses 1 chalk so k = 7. - Student number 3 uses 2 chalk so k = 5. - Student number 0 uses 3 chalk so k = 2. Student number 1 does not have enough chalk, so they will have to replace it.
Constraints:
chalk.length == n1 <= n <= 1051 <= chalk[i] <= 1051 <= k <= 109
Solution: Math
Sum up all the students. k %= sum to skip all the middle rounds.
Time complexity: O(n)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 |
// Author: Huahua class Solution { public: int chalkReplacer(vector<int>& chalk, int k) { long sum = accumulate(begin(chalk), end(chalk), 0L); k %= sum; for (size_t i = 0; i < chalk.size(); ++i) if ((k -= chalk[i]) < 0) return i; return -1; } }; |
Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The ith round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]
Return an array of the most visited sectors sorted in ascending order.
Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).
Example 1:
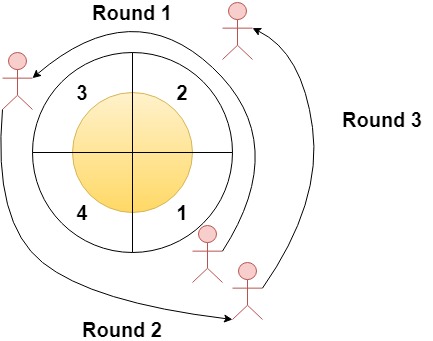
Input: n = 4, rounds = [1,3,1,2] Output: [1,2] Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows: 1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon) We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.
Example 2:
Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2] Output: [2]
Example 3:
Input: n = 7, rounds = [1,3,5,7] Output: [1,2,3,4,5,6,7]
Constraints:
2 <= n <= 1001 <= m <= 100rounds.length == m + 11 <= rounds[i] <= nrounds[i] != rounds[i + 1]for0 <= i < m
Solution: Simulation
Time complexity: O(m*n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
class Solution { public: vector<int> mostVisited(int n, vector<int>& rounds) { vector<int> counts(n); counts[rounds[0] - 1] = 1; for (int i = 1; i < rounds.size(); ++i) for (int s = rounds[i - 1]; ; ++s) { ++counts[s %= n]; if (s == rounds[i] - 1) break; } const int max_count = *max_element(begin(counts), end(counts)); vector<int> ans; for (int i = 0; i < n; ++i) if (counts[i] == max_count) ans.push_back(i + 1); return ans; } }; |