Posts tagged as “search”

花花酱 LeetCode 1368. Minimum Cost to Make at Least One Valid Path in a Grid

By zxi on February 29, 2020

Given a m x ngrid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some invalid signs on the cells of the grid which points outside the grid.

You will initially start at the upper left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path doesn’t have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

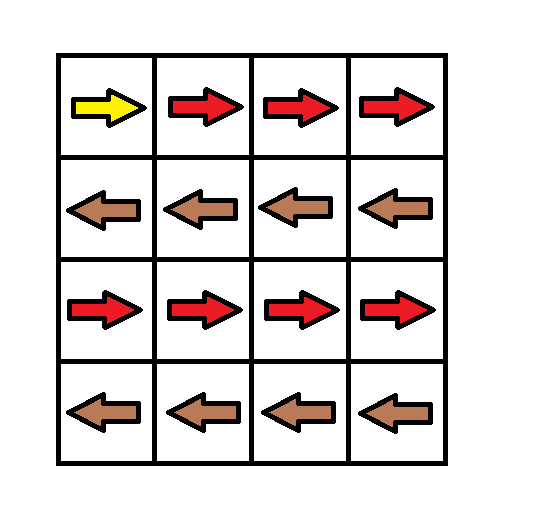
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

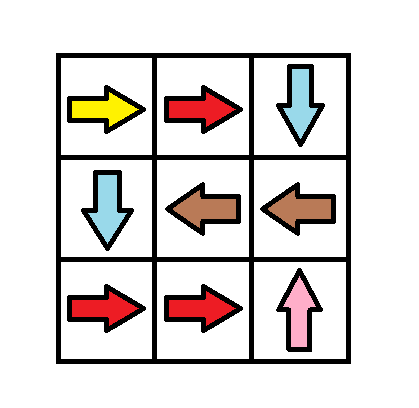
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

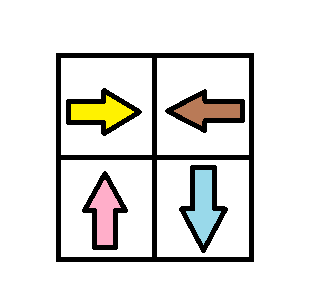
Input: grid = [[1,2],[4,3]]
Output: 1

Example 4:

Input: grid = [[2,2,2],[2,2,2]]
Output: 3

Example 5:

Input: grid = [[4]]
Output: 0

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100

Solution 1: Lazy BFS (fake DP)

dp[i][j] := min steps to reach (i, j)

Time complexity: O((m+n)*m*n)
Space complexity: O(m*n)

C++

// Author: Huahua

class Solution {

public:

int minCost(vector<vector<int>>& grid) {

int m = grid.size();

int n = grid[0].size();

vector<vector<int>> dp(m, vector<int>(n, INT_MAX / 2));

dp[0][0] = 0;

auto solve = [&](int x, int y) {

int& v = dp[y][x];

if (x > 0) v = min(v, dp[y][x - 1] + (grid[y][x - 1] != 1));

if (y > 0) v = min(v, dp[y - 1][x] + (grid[y - 1][x] != 3));

if (x < n - 1) v = min(v, dp[y][x + 1] + (grid[y][x + 1] != 2));

if (y < m - 1) v = min(v, dp[y + 1][x] + (grid[y + 1][x] != 4));

};

// At most m + n steps to propagate the results to (m - 1, n -1).

for (int k = 0; k <= (m + n); ++k) {

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

solve(x, y);

for (int y = m - 1; y >= 0; --y)

for (int x = n - 1; x >= 0; --x)

solve(x, y);

}

return dp[m - 1][n - 1];

}

};

C++

// Author: Huahua, 88 ms / 22.9 MB

class Solution {

public:

int minCost(vector<vector<int>>& grid) {

const int m = grid.size();

const int n = grid[0].size();

vector<vector<int>> dp(m, vector<int>(n, INT_MAX / 2));

dp[0][0] = 0;

while (true) {

auto prev(dp);

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j) {

if (i > 0) dp[i][j] = min(dp[i][j], dp[i - 1][j] + (grid[i - 1][j] != 3));

if (j > 0) dp[i][j] = min(dp[i][j], dp[i][j - 1] + (grid[i][j - 1] != 1));

}

for (int i = m - 1; i >= 0; --i)

for (int j = n - 1; j >= 0; --j) {

if (i != m - 1) dp[i][j] = min(dp[i][j], dp[i + 1][j] + (grid[i + 1][j] != 4));

if (j != n - 1) dp[i][j] = min(dp[i][j], dp[i][j + 1] + (grid[i][j + 1] != 2));

}

if (prev == dp) break; // optimal solution obtained.

}

return dp[m - 1][n - 1];

}

};

Solution 2: 0-1 BFS

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

// Author: Huahua

class Solution {

public:

int minCost(vector<vector<int>>& grid) {

const int m = grid.size();

const int n = grid[0].size();

deque<pair<int, int>> q{{0, 0}};

vector<char> seen(m * n);

vector<vector<int>> dirs{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

while (!q.empty()) {

auto [p, cost] = q.front(); q.pop_front();

int x = p % n, y = p / n;

if (x == n - 1 && y == m - 1) return cost;

if (seen[p]++) continue;

for (int i = 0; i < 4; ++i) {

int tx = x + dirs[i][0], ty = y + dirs[i][1];

int tp = ty * n + tx;

if (tx < 0 || ty < 0 || tx >= n || ty >= m || seen[tp]) continue;

if (grid[y][x] == i + 1)

q.emplace_front(tp, cost);

else

q.emplace_back(tp, cost + 1);

}

return -1;

}

};

花花酱 LeetCode 1306. Jump Game III

By zxi on December 29, 2019

Given an array of non-negative integers arr, you are initially positioned at start index of the array. When you are at index i, you can jump to i + arr[i] or i - arr[i], check if you can reach to any index with value 0.

Notice that you can not jump outside of the array at any time.

Example 1:

Input: arr = [4,2,3,0,3,1,2], start = 5
Output: true
Explanation: 
All possible ways to reach at index 3 with value 0 are: 
index 5 -> index 4 -> index 1 -> index 3 
index 5 -> index 6 -> index 4 -> index 1 -> index 3

Example 2:

Input: arr = [4,2,3,0,3,1,2], start = 0
Output: true 
Explanation: 
One possible way to reach at index 3 with value 0 is: 
index 0 -> index 4 -> index 1 -> index 3

Example 3:

Input: arr = [3,0,2,1,2], start = 2
Output: false
Explanation: There is no way to reach at index 1 with value 0.

Constraints:

1 <= arr.length <= 5 * 10^4
0 <= arr[i] < arr.length
0 <= start < arr.length

Solution: BFS / DFS

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

bool canReach(vector<int>& arr, int start) {

const int n = arr.size();

vector<int> seen(n);

seen[start] = 1;

queue<int> q;

q.push(start);

while (q.size()) {

int cur = q.front();

q.pop();

if (arr[cur] == 0) return true;

for (int i : {-1, 1}) {

int t = cur + i * arr[cur];

if (t < 0 || t >= n || seen[t]) continue;

q.push(t);

seen[t] = 1;

}

return false;

}

};

花花酱 LeetCode 1284. Minimum Number of Flips to Convert Binary Matrix to Zero Matrix

By zxi on December 8, 2019

Given a m x n binary matrix mat. In one step, you can choose one cell and flip it and all the four neighbours of it if they exist (Flip is changing 1 to 0 and 0 to 1). A pair of cells are called neighboors if they share one edge.

Return the minimum number of steps required to convert mat to a zero matrix or -1 if you cannot.

Binary matrix is a matrix with all cells equal to 0 or 1 only.

Zero matrix is a matrix with all cells equal to 0.

Example 1:

Input: mat = [[0,0],[0,1]]
Output: 3
Explanation: One possible solution is to flip (1, 0) then (0, 1) and finally (1, 1) as shown.

Example 2:

Input: mat = [[0]]
Output: 0
Explanation: Given matrix is a zero matrix. We don't need to change it.

Example 3:

Input: mat = [[1,1,1],[1,0,1],[0,0,0]]
Output: 6

Example 4:

Input: mat = [[1,0,0],[1,0,0]]
Output: -1
Explanation: Given matrix can't be a zero matrix

Constraints:

m == mat.length
n == mat[0].length
1 <= m <= 3
1 <= n <= 3
mat[i][j] is 0 or 1.

Solution: BFS + bitmask

Time complexity: O(2^(m*n))
Space complexity: O(2^(m*n))

C++

// Author: Huahua

class Solution {

public:

int minFlips(vector<vector<int>>& mat) {

const int m = mat.size();

const int n = mat[0].size();

const vector<int> dirs{0, 1, 0, -1, 0, 0};

auto flip = [&](int s, int x, int y) {

for (int i = 0; i < 5; ++i) {

const int tx = x + dirs[i];

const int ty = y + dirs[i + 1];

if (tx < 0 || tx >= n || ty < 0 || ty >= m) continue;

s ^= (1 << ty * n + tx);

}

return s;

};

int steps = 0;

queue<int> q;

vector<int> seen(1 << (n * m));

int start = 0;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

start |= (mat[y][x] << (y * n + x));

q.push(start);

seen[start] = 1;

while (!q.empty()) {

int size = q.size();

while (size--) {

int s = q.front();

if (s == 0) return steps;

q.pop();

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x) {

int t = flip(s, x, y);

if (seen[t]) continue;

seen[t] = 1;

q.push(t);

}

++steps;

}

return -1;

}

};

花花酱 LeetCode 1263. Minimum Moves to Move a Box to Their Target Location

By zxi on November 26, 2019

Storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.

The game is represented by a grid of size n*m, where each element is a wall, floor, or a box.

Your task is move the box 'B' to the target position 'T' under the following rules:

Player is represented by character 'S' and can move up, down, left, right in the grid if it is a floor (empy cell).
Floor is represented by character '.' that means free cell to walk.
Wall is represented by character '#' that means obstacle (impossible to walk there).
There is only one box 'B' and one target cell 'T' in the grid.
The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
The player cannot walk through the box.

Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.

Example 1:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#",".","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.

Example 2:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#","#","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: -1

Example 3:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T",".",".","#","#"],
               ["#",".","#","B",".","#"],
               ["#",".",".",".",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 5
Explanation:  push the box down, left, left, up and up.

Example 4:

Input: grid = [["#","#","#","#","#","#","#"],
               ["#","S","#",".","B","T","#"],
               ["#","#","#","#","#","#","#"]]
Output: -1

Constraints:

1 <= grid.length <= 20
1 <= grid[i].length <= 20
grid contains only characters '.', '#', 'S' , 'T', or 'B'.
There is only one character 'S', 'B' and 'T' in the grid.

Solution: BFS + DFS

BFS to search by push steps to find miminal number of pushes. Each time we move from the previous position (initial position or last push position) to a new push position. Use DFS to check that whether that path exist or not.

C++

// Author: Huahua

struct Node {

int bx;

int by;

int px;

int py;

int key() const { return ((by * 20 + bx) << 16) | (py * 20 + px); }

};

class Solution {

public:

int minPushBox(vector<vector<char>>& grid) {

const int n = grid.size();

const int m = grid[0].size();

Node start;

Node end;

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x)

if (grid[y][x] == 'B') {

start.bx = x;

start.by = y;

} else if (grid[y][x] == 'S') {

start.px = x;

start.py = y;

} else if (grid[y][x] == 'T') {

end.bx = x;

end.by = y;

}

auto hasPath = [&](const Node& cur, int tx, int ty) {

vector<int> seen(m*n);

function<bool(int, int)> dfs = [&](int x, int y) {

if (x < 0 || x >= m || y < 0 || y >= n || grid[y][x] == '#')

return false;

if (x == cur.bx && y == cur.by) return false;

int key = y * m + x;

if (seen[key]) return false;

seen[key] = 1;

if (x == tx && y == ty) return true;

return dfs(x + 1, y) || dfs(x - 1, y) || dfs(x, y + 1) || dfs(x, y - 1);

};

return dfs(cur.px, cur.py);

};

auto canPush = [&](const Node& cur, int dx, int dy, Node* nxt) {

const int bx = cur.bx + dx;

const int by = cur.by + dy;

if (bx < 0 || bx >= m || by < 0 || by >= n || grid[by][bx] == '#')

return false;

if (!hasPath(cur, cur.bx - dx, cur.by - dy)) return false;

nxt->bx = bx;

nxt->by = by;

nxt->px = cur.bx;

nxt->py = cur.by;

return true;

};

const vector<int> dirs{0, -1, 0, 1, 0};

unordered_set<int> seen;

queue<Node> q;

q.push(start);

int steps = 0;

while (q.size()) {

int size = q.size();

while (size--) {

Node cur = q.front();

q.pop();

for (int i = 0; i < 4; ++i) {

Node nxt;

if (!canPush(cur, dirs[i], dirs[i + 1], &nxt) ||

seen.count(nxt.key()))

continue;

if (nxt.bx == end.bx && nxt.by == end.by) return steps + 1;

seen.insert(nxt.key());

q.push(nxt);

}

++steps;

}

return -1;

}

};

**Solution: A* + BFS**

g : history = # of pushes
h: heuristics = Manhattan distance from the current box position to the target position, always <= actual moves.
f = g + h

C++

100

101

// Author: Huahua, 4 ms, 17.5 MB

struct Node {

int bx;

int by;

int px;

int py;

int h;

int g;

int key() const {

return ((by * m + bx) << 2) | ((bx - px) + 1) | ((by - py) + 1) >> 1;

}

int f() const { return g + h; }

bool operator< (const Node& o) const {

return f() > o.f();

}

static int m;

};

int Node::m;

class Solution {

public:

int minPushBox(vector<vector<char>>& grid) {

const vector<int> dirs{0, -1, 0, 1, 0};

const int n = grid.size();

const int m = Node::m = grid[0].size();

Node start;

Node end;

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x)

if (grid[y][x] == 'B') {

start.bx = x;

start.by = y;

} else if (grid[y][x] == 'S') {

start.px = x;

start.py = y;

} else if (grid[y][x] == 'T') {

end.bx = x;

end.by = y;

}

auto isValid = [&](int x, int y) {

return !(x < 0 || x >= m || y < 0 || y >= n || grid[y][x] == '#');

};

auto hasPath = [&](const Node& cur, int tx, int ty) {

if (!isValid(tx, ty)) return false;

vector<int> seen(m*n);

queue<int> q;

q.push(cur.py * m + cur.px);

seen[cur.py * m + cur.px] = 1;

while (q.size()) {

int x = q.front() % m;

int y = q.front() / m;

q.pop();

for (int i = 0; i < 4; ++i) {

int nx = x + dirs[i];

int ny = y + dirs[i + 1];

if (!isValid(nx, ny)) continue;

if (nx == cur.bx && ny == cur.by) continue;

if (nx == tx && ny == ty) return true;

if (seen[ny * m + nx]++) continue;

q.push(ny * m + nx);

}

return false;

};

auto canPush = [&](const Node& cur, int dx, int dy, Node* nxt) {

nxt->bx = cur.bx + dx;

nxt->by = cur.by + dy;

nxt->px = cur.bx;

nxt->py = cur.by;

nxt->g = cur.g + 1;

nxt->h = abs(nxt->bx - end.bx) + abs(nxt->by - end.by);

if (!isValid(nxt->bx, nxt->by)) return false;

return hasPath(cur, cur.bx - dx, cur.by - dy);

};

vector<int> seen(m*n*4);

priority_queue<Node> q;

start.g = 0;

start.h = abs(start.bx - end.bx) + abs(start.by - end.by);

q.push(start);

while (q.size()) {

Node cur = q.top();

q.pop();

for (int i = 0; i < 4; ++i) {

Node nxt;

if (!canPush(cur, dirs[i], dirs[i + 1], &nxt) || seen[nxt.key()]++) continue;

if (nxt.bx == end.bx && nxt.by == end.by) return nxt.g;

q.push(nxt);

}

return -1;

}

};

花花酱 LeetCode 1255. Maximum Score Words Formed by Letters

By zxi on November 9, 2019

Given a list of words, list of single letters (might be repeating) and score of every character.

Return the maximum score of any valid set of words formed by using the given letters (words[i] cannot be used two or more times).

It is not necessary to use all characters in letters and each letter can only be used once. Score of letters 'a', 'b', 'c', … ,'z' is given by score[0], score[1], … , score[25] respectively.

Example 1:

Input: words = ["dog","cat","dad","good"], letters = ["a","a","c","d","d","d","g","o","o"], score = [1,0,9,5,0,0,3,0,0,0,0,0,0,0,2,0,0,0,0,0,0,0,0,0,0,0]
Output: 23
Explanation:
Score  a=1, c=9, d=5, g=3, o=2
Given letters, we can form the words "dad" (5+1+5) and "good" (3+2+2+5) with a score of 23.
Words "dad" and "dog" only get a score of 21.

Example 2:

Input: words = ["xxxz","ax","bx","cx"], letters = ["z","a","b","c","x","x","x"], score = [4,4,4,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,5,0,10]
Output: 27
Explanation:
Score  a=4, b=4, c=4, x=5, z=10
Given letters, we can form the words "ax" (4+5), "bx" (4+5) and "cx" (4+5) with a score of 27.
Word "xxxz" only get a score of 25.

Example 3:

Input: words = ["leetcode"], letters = ["l","e","t","c","o","d"], score = [0,0,1,1,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,1,0,0,0,0,0,0]
Output: 0
Explanation:
Letter "e" can only be used once.

Constraints:

1 <= words.length <= 14
1 <= words[i].length <= 15
1 <= letters.length <= 100
letters[i].length == 1
score.length == 26
0 <= score[i] <= 10
words[i], letters[i] contains only lower case English letters.

Solution: Combination

Time complexity: O(2^n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maxScoreWords(vector<string>& words, vector<char>& letters, vector<int>& score) {

vector<int> counts(26);

vector<int> scores(words.size());

for (char c : letters) ++counts[c - 'a'];

for (int i = 0; i < words.size(); ++i)

for (char c : words[i]) scores[i] += score[c - 'a'];

int ans = 0;

function<void(int, int)> dfs = [&](int s, int cur) {

if (cur > ans) ans = cur;

for (int i = s; i < words.size(); ++i) {

bool valid = true;

for (char c : words[i]) valid &= --counts[c - 'a'] >= 0;

if (valid) dfs(i + 1, cur + scores[i]);

for (char c : words[i]) ++counts[c - 'a'];

}

};

dfs(0, 0);

return ans;

}

};