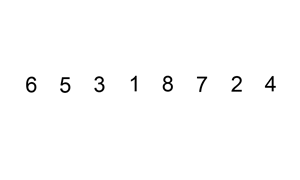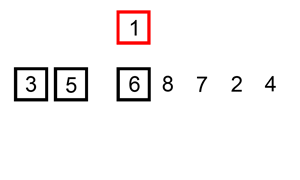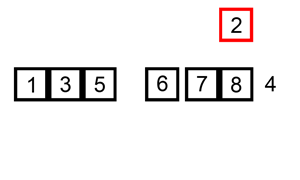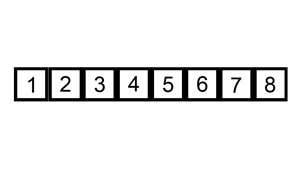You are given a 0-indexed integer array nums, where nums[i] represents the score of the ith student. You are also given an integer k.
Pick the scores of any k students from the array so that the difference between the highest and the lowest of the k scores is minimized.
Return the minimum possible difference.
Example 1:
Input: nums = [90], k = 1 Output: 0 Explanation: There is one way to pick score(s) of one student: - [90]. The difference between the highest and lowest score is 90 - 90 = 0. The minimum possible difference is 0.
Example 2:
Input: nums = [9,4,1,7], k = 2 Output: 2 Explanation: There are six ways to pick score(s) of two students: - [9,4,1,7]. The difference between the highest and lowest score is 9 - 4 = 5. - [9,4,1,7]. The difference between the highest and lowest score is 9 - 1 = 8. - [9,4,1,7]. The difference between the highest and lowest score is 9 - 7 = 2. - [9,4,1,7]. The difference between the highest and lowest score is 4 - 1 = 3. - [9,4,1,7]. The difference between the highest and lowest score is 7 - 4 = 3. - [9,4,1,7]. The difference between the highest and lowest score is 7 - 1 = 6. The minimum possible difference is 2.
Constraints:
1 <= k <= nums.length <= 10000 <= nums[i] <= 105
Solution: Sliding Window
Sort the array, to minimize the difference, k numbers must be consecutive (i.e, from a subarray). We use a sliding window size of k and try all possible subarrays.
Ans = min{(nums[k – 1] – nums[0]), (nums[k] – nums[1]), … (nums[n – 1] – nums[n – k])}
Time complexity: O(nlogn)
Space complexity: O(1)
C++
|
1 2 3 4 5 6 7 8 9 10 11 |
// Author: Huahua class Solution { public: int minimumDifference(vector<int>& nums, int k) { int ans = INT_MAX; sort(begin(nums), end(nums)); for (int i = k - 1; i < nums.size(); ++i) ans = min(ans, nums[i] - nums[i - k + 1]); return ans; } }; |