Posts tagged as “subarray”

花花酱 LeetCode 410. Split Array Largest Sum

By zxi on July 3, 2018

Problem

Given an array which consists of non-negative integers and an integer m, you can split the array into m non-empty continuous subarrays. Write an algorithm to minimize the largest sum among these m subarrays.

Note:
If n is the length of array, assume the following constraints are satisfied:

1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)

Examples:

Input:
nums = [7,2,5,10,8]
m = 2

Output:
18

Explanation:
There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8],
where the largest sum among the two subarrays is only 18.

Solution: DP

Time complexity: O(n^2*m)

Space complexity: O(n*m)

C++ / Recursion + Memorization

// Author: Huahua

// Running time: 111 ms

class Solution {

public:

int splitArray(vector<int>& nums, int m) {

const int n = nums.size();

sums_ = vector<int>(n);

mem_ = vector<vector<int>>(n, vector<int>(m + 1, INT_MAX));

sums_[0] = nums[0];

for (int i = 1; i < n; ++i)

sums_[i] = sums_[i - 1] + nums[i];

return splitArray(nums, n - 1, m);

}

private:

vector<vector<int>> mem_;

vector<int> sums_;

// min of largest sum of spliting nums[0] ~ nums[k] into m groups

int splitArray(const vector<int>& nums, int k, int m) {

if (m == 1) return sums_[k];

if (m > k + 1) return INT_MAX;

if (mem_[k][m] != INT_MAX) return mem_[k][m];

int ans = INT_MAX;

for (int i = 0; i < k; ++i)

ans = min(ans, max(splitArray(nums, i, m - 1), sums_[k] - sums_[i]));

return mem_[k][m] = ans;

}

};

C++ / DP

// Author: Huahua

// Running time: 90 ms

class Solution {

public:

int splitArray(vector<int>& nums, int m) {

const int n = nums.size();

vector<int> sums(n);

// dp[i][j] := min of largest sum of splitting nums[0] ~ nums[j] into i groups.

vector<vector<int>> dp(m + 1, vector<int>(n, INT_MAX));

sums[0] = nums[0];

for (int i = 1; i < n; ++i)

sums[i] = sums[i - 1] + nums[i];

for (int i = 0; i < n; ++i)

dp[1][i] = sums[i];

for (int i = 2; i <= m; ++i)

for (int j = i - 1; j < n; ++j)

for (int k = 0; k < j; ++k)

dp[i][j] = min(dp[i][j], max(dp[i - 1][k], sums[j] - sums[k]));

return dp[m][n - 1];

}

};

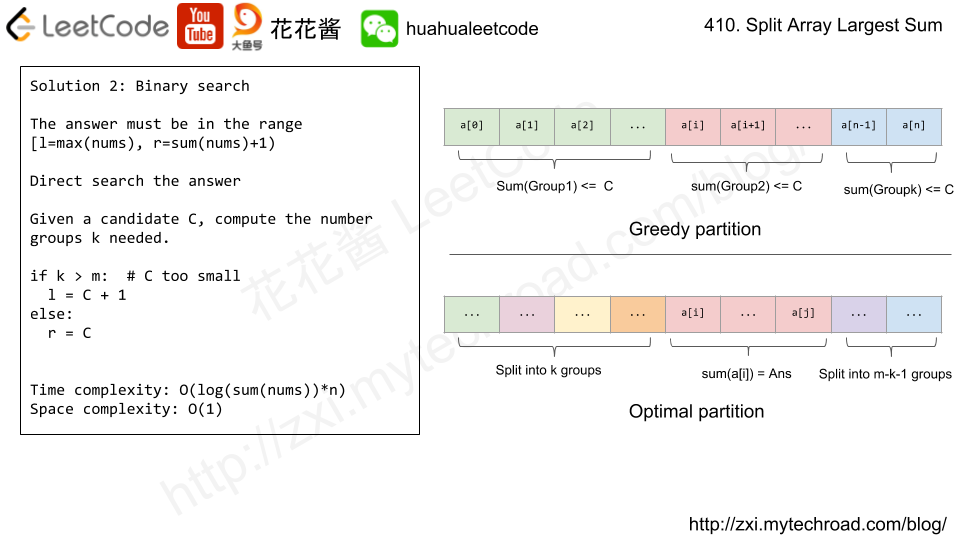
Solution: Binary Search

Time complexity: O(log(sum(nums))*n)

Space complexity: O(1)

// Author: Huahua

// Running time: 3 ms

class Solution {

public:

int splitArray(vector<int>& nums, int m) {

long l = *max_element(begin(nums), end(nums));

long r = accumulate(begin(nums), end(nums), 0L) + 1;

while (l < r) {

long limit = (r - l) / 2 + l;

if (min_groups(nums, limit) > m)

l = limit + 1;

else

r = limit;

}

return l;

}

private:

int min_groups(const vector<int>& nums, long limit) {

long sum = 0;

int groups = 1;

for (int num : nums) {

if (sum + num > limit) {

sum = num;

++groups;

} else {

sum += num;

}

return groups;

}

};

花花酱 LeetCode 845. Longest Mountain in Array

By zxi on June 3, 2018

Problem

题目大意：找出最长的山形子数组。

https://leetcode.com/problems/longest-mountain-in-array/description/

Let’s call any (contiguous) subarray B (of A) a mountain if the following properties hold:

B.length >= 3
There exists some 0 < i < B.length - 1 such that B[0] < B[1] < ... B[i-1] < B[i] > B[i+1] > ... > B[B.length - 1]

(Note that B could be any subarray of A, including the entire array A.)

Given an array A of integers, return the length of the longest mountain.

Return 0 if there is no mountain.

Example 1:

Input: [2,1,4,7,3,2,5]
Output: 5
Explanation: The largest mountain is [1,4,7,3,2] which has length 5.

Example 2:

Input: [2,2,2]
Output: 0
Explanation: There is no mountain.

Note:

0 <= A.length <= 10000
0 <= A[i] <= 10000

Solution: DP

Three passes

Time complexity: O(n)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 24 ms

class Solution {

public:

int longestMountain(vector<int>& A) {

vector<int> inc(A.size());

vector<int> dec(A.size());

for (int i = 1; i < A.size(); ++i)

if (A[i] > A[i - 1]) inc[i] = inc[i - 1] + 1;

for (int i = A.size() - 2; i > 0; --i)

if (A[i] > A[i + 1]) dec[i] = dec[i + 1] + 1;

int ans = 0;

for (int i = 0; i < A.size(); ++i)

if (inc[i] && dec[i])

ans = max(ans, inc[i] + dec[i] + 1);

return ans >= 3 ? ans : 0;

}

};

One pass

Time complexity: O(n)

Space complexity: O(1)

// Author: Huahua

// Running time: 24 ms

class Solution {

public:

int longestMountain(vector<int>& A) {

int inc = 0;

int dec = 0;

int ans = 0;

for (int i = 1; i < A.size(); ++i) {

if (dec && A[i] > A[i - 1] || A[i] == A[i - 1])

dec = inc = 0;

inc += A[i] > A[i - 1];

dec += A[i] < A[i - 1];

if (inc && dec)

ans = max(ans, inc + dec + 1);

}

return ans >= 3 ? ans : 0;

}

};

花花酱 LeetCode 413. Arithmetic Slices

By zxi on March 17, 2018

题目大意：返回所有子数组中等差数列的个数。

Problem

https://leetcode.com/problems/arithmetic-slices/description/

A sequence of number is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.

For example, these are arithmetic sequence:

1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9

The following sequence is not arithmetic.

1, 1, 2, 5, 7

A zero-indexed array A consisting of N numbers is given. A slice of that array is any pair of integers (P, Q) such that 0 <= P < Q < N.

A slice (P, Q) of array A is called arithmetic if the sequence:
A[P], A[p + 1], …, A[Q – 1], A[Q] is arithmetic. In particular, this means that P + 1 < Q.

The function should return the number of arithmetic slices in the array A.

Example:

A = [1, 2, 3, 4]

return: 3, for 3 arithmetic slices in A: [1, 2, 3], [2, 3, 4] and [1, 2, 3, 4] itself.

Solution 0: Reduction

Reduce the problem to # of all 1 sub arrays.

B[i – 2] = is_slice(A[i], A[i+1], A[i+2])

Time Complexity: O(n)

Space Complexity: O(n)

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numberOfArithmeticSlices(vector<int>& A) {

if (A.size() < 3) return 0;

vector<int> B(A.size() - 2, 0);

for (int i = 2; i < A.size() ; ++i) {

if (A[i - 1] - A[i - 2] == A[i] - A[i - 1])

B[i - 2] = 1;

}

return all1SubArrays(B);

}

private:

// return number of arrays whose values are all ones.

int all1SubArrays(const vector<int>& A) {

int sum = 0;

int curr = 0;

for (int i = 0; i < A.size(); ++i)

if (A[i]) sum += ++curr;

else curr = 0;

return sum;

}

};

Solution 1: Combined

C++

Time complexity: O(n)

Space complexity: O(1)

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int numberOfArithmeticSlices(vector<int>& A) {

int sum = 0;

int curr = 0;

for (int i = 2; i < A.size() ; ++i) {

if (A[i - 1] - A[i - 2] == A[i] - A[i - 1]) {

sum += ++curr;

} else {

curr = 0;

}

return sum;

}

};

Posts tagged as “subarray”

花花酱 LeetCode 410. Split Array Largest Sum

Problem

Solution: DP

Solution: Binary Search

花花酱 LeetCode 845. Longest Mountain in Array

Problem

Solution: DP

花花酱 LeetCode 413. Arithmetic Slices

Problem

Example:

Solution 0: Reduction

Solution 1: Combined

Related Problems:

花花酱 LeetCode 795. Number of Subarrays with Bounded Maximum

花花酱 LeetCode 654. Maximum Binary Tree