Posts tagged as “xor”

花花酱 LeetCode 1442. Count Triplets That Can Form Two Arrays of Equal XOR

By zxi on May 11, 2020

Given an array of integers arr.

We want to select three indices i, j and k where (0 <= i < j <= k < arr.length).

Let’s define a and b as follows:

a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]
b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]

Note that ^ denotes the bitwise-xor operation.

Return the number of triplets (i, j and k) Where a == b.

Example 1:

Input: arr = [2,3,1,6,7]
Output: 4
Explanation: The triplets are (0,1,2), (0,2,2), (2,3,4) and (2,4,4)

Example 2:

Input: arr = [1,1,1,1,1]
Output: 10

Example 3:

Input: arr = [2,3]
Output: 0

Example 4:

Input: arr = [1,3,5,7,9]
Output: 3

Example 5:

Input: arr = [7,11,12,9,5,2,7,17,22]
Output: 8

Constraints:

1 <= arr.length <= 300
1 <= arr[i] <= 10^8

Solution 1: Brute Force (TLE)

Time complexity: O(n^4)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countTriplets(vector<int>& arr) {

const int n = arr.size();

int ans = 0;

for (int i = 0; i < n; ++i)

for (int j = i + 1; j < n; ++j)

for (int k = j; k < n; ++k) {

int a = 0;

int b = 0;

for (int t = i; t < j; ++t)

a ^= arr[t];

for (int t = j; t <= k; ++t)

b ^= arr[t];

if (a == b) ++ans;

}

return ans;

}

};

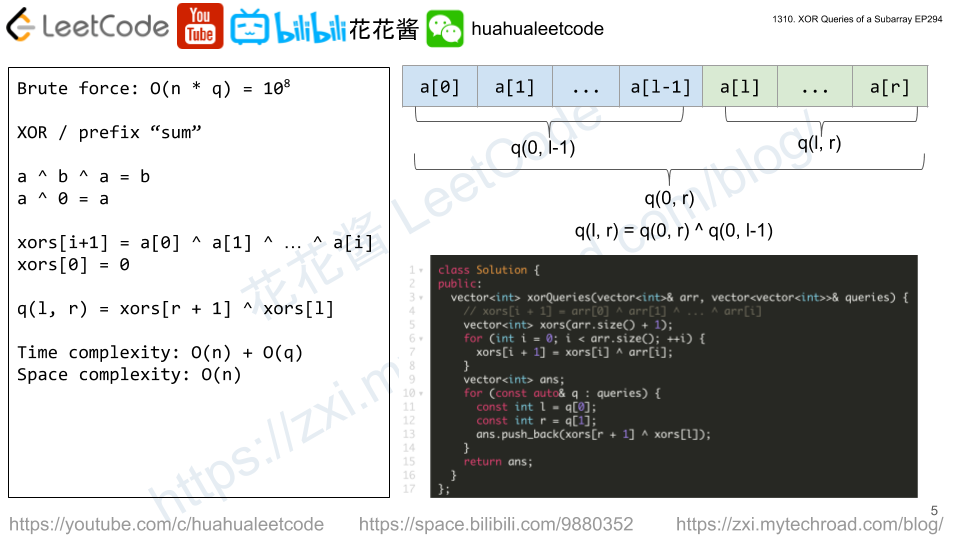
Solution 2: Prefix XORs

Let xors[i] = arr[0] ^ arr[1] ^ … ^ arr[i-1]
arr[i] ^ arr[i + 1] ^ … ^ arr[j – 1] = (arr[0] ^ … ^ arr[j – 1]) ^ (arr[0] ^ … ^ arr[i-1]) = xors[j] ^ xors[i]

We then can compute a and b in O(1) time.

Time complexity: O(n^3)
Space complexity: O(n)

C++

// Author: Huahua, 232 ms

class Solution {

public:

int countTriplets(vector<int>& arr) {

const int n = arr.size();

int ans = 0;

vector<int> xors(n + 1);

for (int i = 0; i < n; ++i)

xors[i + 1] = xors[i] ^ arr[i];

for (int i = 0; i < n; ++i)

for (int j = i + 1; j < n; ++j)

for (int k = j; k < n; ++k) {

const int a = xors[j] ^ xors[i];

const int b = xors[k + 1] ^ xors[j];

if (a == b) ++ans;

}

return ans;

}

};

Solution 3: Prefix XORs II

a = arr[i] ^ arr[i + 1] ^ … ^ arr[j – 1]
b = arr[j] ^ arr[j + 1] ^ … ^ arr[k]
a == b => a ^ b == 0
XORs(i ~ k) == 0
XORS(0 ~ k) ^ XORs(0 ~ i – 1) = 0

Problem => find all pairs of (i – 1, k) such that xors[k+1] == xors[i]
For each pair (i – 1, k), there are k – i positions we can insert j.

Time complexity: O(n^2)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countTriplets(vector<int>& arr) {

const int n = arr.size();

int ans = 0;

vector<int> xors(n + 1);

for (int i = 0; i < n; ++i)

xors[i + 1] = xors[i] ^ arr[i];

for (int i = 0; i < n; ++i)

for (int k = i + 1; k < n; ++k)

if (xors[k + 1] == xors[i])

ans += k - i;

return ans;

}

};

Solution 3: HashTable

Similar to target sum, use a hashtable to store the frequency of each prefix xors.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

// Author: Huahua 4 ms

class Solution {

public:

int countTriplets(vector<int>& arr) {

const int n = arr.size();

int ans = 0;

unordered_map<int, int> freq{{0, 1}};

unordered_map<int, int> sum;

int X = 0;

for (int i = 0; i < n; ++i) {

X ^= arr[i];

ans += freq[X] * i - sum[X];

++freq[X];

sum[X] += i + 1;

}

return ans;

}

};

花花酱 LeetCode 1310. XOR Queries of a Subarray

By zxi on January 5, 2020

Given the array arr of positive integers and the array queries where queries[i] = [L_i,R_i], for each query i compute the XOR of elements from L_i to Ri (that is, arr[L_i] xor arr[L_i+1] xor ... xor arr[R_i] ). Return an array containing the result for the given queries.

Example 1:

Input: arr = [1,3,4,8], queries = [[0,1],[1,2],[0,3],[3,3]]
Output: [2,7,14,8] 
Explanation: 
The binary representation of the elements in the array are:
1 = 0001 
3 = 0011 
4 = 0100 
8 = 1000 
The XOR values for queries are:
[0,1] = 1 xor 3 = 2 
[1,2] = 3 xor 4 = 7 
[0,3] = 1 xor 3 xor 4 xor 8 = 14 
[3,3] = 8

Example 2:

Input: arr = [4,8,2,10], queries = [[2,3],[1,3],[0,0],[0,3]]
Output: [8,0,4,4]

Constraints:

1 <= arr.length <= 3 * 10^4
1 <= arr[i] <= 10^9
1 <= queries.length <= 3 * 10^4
queries[i].length == 2
0 <= queries[i][0] <= queries[i][1] < arr.length

Solution: Prefix Sum

Time complexity: O(n) + O(q)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> xorQueries(vector<int>& arr, vector<vector<int>>& queries) {

// xors[i + 1] = arr[0] ^ arr[1] ^ ... ^ arr[i]

vector<int> xors(arr.size() + 1);

for (int i = 0; i < arr.size(); ++i) {

xors[i + 1] = xors[i] ^ arr[i];

}

vector<int> ans;

for (const auto& q : queries) {

const int l = q[0];

const int r = q[1];

ans.push_back(xors[r + 1] ^ xors[l]);

}

return ans;

}

};

tby

花花酱 LeetCode 1252. Cells with Odd Values in a Matrix

By zxi on November 9, 2019

Given n and m which are the dimensions of a matrix initialized by zeros and given an array indices where indices[i] = [ri, ci]. For each pair of [ri, ci] you have to increment all cells in row ri and column ci by 1.

Return the number of cells with odd values in the matrix after applying the increment to all indices.

Example 1:

Input: n = 2, m = 3, indices = [[0,1],[1,1]]
Output: 6
Explanation: Initial matrix = [[0,0,0],[0,0,0]].
After applying first increment it becomes [[1,2,1],[0,1,0]].
The final matrix will be [[1,3,1],[1,3,1]] which contains 6 odd numbers.

Example 2:

Input: n = 2, m = 2, indices = [[1,1],[0,0]]
Output: 0
Explanation: Final matrix = [[2,2],[2,2]]. There is no odd number in the final matrix.

Constraints:

1 <= n <= 50
1 <= m <= 50
1 <= indices.length <= 100
0 <= indices[i][0] < n
0 <= indices[i][1] < m

Solution 1: Simulation

Time complexity: O((n+m)*k + n*m)
Space complexity: O(n*m)

C++

// Author: Huahua

class Solution {

public:

int oddCells(int n, int m, vector<vector<int>>& indices) {

vector<vector<int>> a(n, vector<int>(m));

for (const auto& idx : indices) {

for (int x = 0; x < m; ++x) ++a[idx[0]][x];

for (int y = 0; y < n; ++y) ++a[y][idx[1]];

}

int ans = 0;

for (int i = 0; i < n; ++i)

for (int j = 0; j < m; ++j)

ans += a[i][j] & 1;

return ans;

}

};

Solution 2: Counting

For each row and column, compute how many times it will be increased (odd or even).
For each a[i][j], check how many times the i-th row and j-th column were increased, if the sum is odd then a[i][j] will odd.
Time complexity: O(n*m + k)
Space complexity: O(n+m)

C++

// Author: Huahua

class Solution {

public:

int oddCells(int n, int m, vector<vector<int>>& indices) {

vector<int> cols(m);

vector<int> rows(n);

for (const auto& idx : indices) {

rows[idx[0]] ^= 1;

cols[idx[1]] ^= 1;

}

int ans = 0;

for (int i = 0; i < n; ++i)

for (int j = 0; j < m; ++j)

ans += rows[i] ^ cols[j];

return ans;

}

};

花花酱 LeetCode 810. Chalkboard XOR Game

By zxi on May 2, 2018

Problem

We are given non-negative integers nums[i] which are written on a chalkboard. Alice and Bob take turns erasing exactly one number from the chalkboard, with Alice starting first. If erasing a number causes the bitwise XOR of all the elements of the chalkboard to become 0, then that player loses. (Also, we’ll say the bitwise XOR of one element is that element itself, and the bitwise XOR of no elements is 0.)

Also, if any player starts their turn with the bitwise XOR of all the elements of the chalkboard equal to 0, then that player wins.

Return True if and only if Alice wins the game, assuming both players play optimally.

Example:
Input: nums = [1, 1, 2]
Output: false
Explanation: 
Alice has two choices: erase 1 or erase 2. 
If she erases 1, the nums array becomes [1, 2]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 2 = 3. Now Bob can remove any element he wants, because Alice will be the one to erase the last element and she will lose. 
If Alice erases 2 first, now nums becomes [1, 1]. The bitwise XOR of all the elements of the chalkboard is 1 XOR 1 = 0. Alice will lose.

Notes:

1 <= N <= 1000.
0 <= nums[i] <= 2^16.

Solution: Math

Time complexity: O(n)

Space complexity: O(1)

// Author: Huahua

// Running time: 15 ms

class Solution {

public:

bool xorGame(vector<int>& nums) {

if (nums.size() % 2 == 0) return true;

int x = 0;

for (int num : nums) x ^= num;

return x == 0;

}

};

花花酱 LeetCode 627. Swap Salary

By zxi on April 3, 2018

Problem

https://leetcode.com/problems/swap-salary/description/

Given a table salary, such as the one below, that has m=male and f=female values. Swap all f and m values (i.e., change all f values to m and vice versa) with a single update query and no intermediate temp table.For example:

| id | name | sex | salary |
|----|------|-----|--------|
| 1  | A    | m   | 2500   |
| 2  | B    | f   | 1500   |
| 3  | C    | m   | 5500   |
| 4  | D    | f   | 500    |

After running your query, the above salary table should have the following rows:

| id | name | sex | salary |
|----|------|-----|--------|
| 1  | A    | f   | 2500   |
| 2  | B    | m   | 1500   |
| 3  | C    | f   | 5500   |
| 4  | D    | m   | 500    |

Solution: XOR

# Author: Huahua

# Running time: 309 ms

update salary set sex = char(ascii('f') ^ ascii('m') ^ ascii(sex))