Posts published in “Binary Search”

花花酱 LeetCode 2141. Maximum Running Time of N Computers

By zxi on January 30, 2022

You have n computers. You are given the integer n and a 0-indexed integer array batteries where the i^th battery can run a computer for batteries[i] minutes. You are interested in running all n computers simultaneously using the given batteries.

Initially, you can insert at most one battery into each computer. After that and at any integer time moment, you can remove a battery from a computer and insert another battery any number of times. The inserted battery can be a totally new battery or a battery from another computer. You may assume that the removing and inserting processes take no time.

Note that the batteries cannot be recharged.

Return the maximum number of minutes you can run all the n computers simultaneously.

Example 1:

Input: n = 2, batteries = [3,3,3]
Output: 4
Explanation: 
Initially, insert battery 0 into the first computer and battery 1 into the second computer.
After two minutes, remove battery 1 from the second computer and insert battery 2 instead. Note that battery 1 can still run for one minute.
At the end of the third minute, battery 0 is drained, and you need to remove it from the first computer and insert battery 1 instead.
By the end of the fourth minute, battery 1 is also drained, and the first computer is no longer running.
We can run the two computers simultaneously for at most 4 minutes, so we return 4.

Example 2:

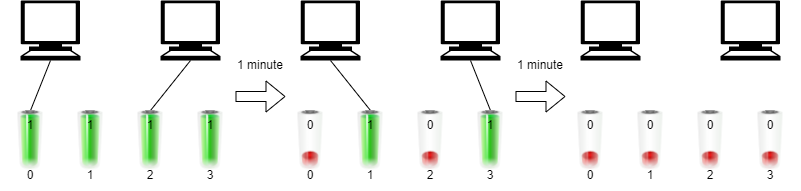
Input: n = 2, batteries = [1,1,1,1]
Output: 2
Explanation: 
Initially, insert battery 0 into the first computer and battery 2 into the second computer. 
After one minute, battery 0 and battery 2 are drained so you need to remove them and insert battery 1 into the first computer and battery 3 into the second computer. 
After another minute, battery 1 and battery 3 are also drained so the first and second computers are no longer running.
We can run the two computers simultaneously for at most 2 minutes, so we return 2.

Constraints:

1 <= n <= batteries.length <= 10⁵
1 <= batteries[i] <= 10⁹

Solution: Binary Search

Find the smallest L that we can not run, ans = L – 1.

For a guessing m, we check the total battery powers T = sum(min(m, batteries[i])), if T >= m * n, it means there is a way (doesn’t need to figure out how) to run n computers for m minutes by fully unitize those batteries.

Proof: If T >= m*n holds, there are two cases:

There are only n batteries, can not swap, but each of them has power >= m.
At least one of the batteries have power less than m, but there are more than n batteries and total power is sufficient, we can swap them with others.

Time complexity: O(Slogn) where S = sum(batteries)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

long long maxRunTime(int n, vector<int>& batteries) {

long long l = 0;

long long r = accumulate(begin(batteries), end(batteries), 0LL) + 1;

while (l < r) {

long long m = l + (r - l) / 2;

long long t = 0;

for (long long b : batteries)

t += min(m, b);

if (m * n > t) // smallest m that does not fit.

r = m;

else

l = m + 1;

}

return l - 1; // greatest m that fits.

}

};

花花酱 LeetCode 1995. Count Special Quadruplets

By zxi on December 31, 2021

Given a 0-indexed integer array nums, return the number of distinct quadruplets (a, b, c, d) such that:

nums[a] + nums[b] + nums[c] == nums[d], and
a < b < c < d

Example 1:

Input: nums = [1,2,3,6]
Output: 1
Explanation: The only quadruplet that satisfies the requirement is (0, 1, 2, 3) because 1 + 2 + 3 == 6.

Example 2:

Input: nums = [3,3,6,4,5]
Output: 0
Explanation: There are no such quadruplets in [3,3,6,4,5].

Example 3:

Input: nums = [1,1,1,3,5]
Output: 4
Explanation: The 4 quadruplets that satisfy the requirement are:
- (0, 1, 2, 3): 1 + 1 + 1 == 3
- (0, 1, 3, 4): 1 + 1 + 3 == 5
- (0, 2, 3, 4): 1 + 1 + 3 == 5
- (1, 2, 3, 4): 1 + 1 + 3 == 5

Constraints:

4 <= nums.length <= 50
1 <= nums[i] <= 100

Solution 1: Brute force (224ms)

Enumerate a, b, c, d.

Time complexity: O(C(n, 4)) = O(n⁴/24)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countQuadruplets(vector<int>& nums) {

const int n = nums.size();

int ans = 0;

for (int a = 0; a < n; ++a)

for (int b = a + 1; b < n; ++b)

for (int c = b + 1; c < n; ++c)

for (int d = c + 1; d < n; ++d)

ans += nums[a] + nums[b] + nums[c] == nums[d];

return ans;

}

};

Solution 2: Static frequency table + binary search (39ms)

For each element, we store its indices (sorted).

Given a, b, c, target t = nums[a] + nums[b] + nums[c], we check the hashtable and use binary search to find how many times it occurred after index c.

Time complexity: O(n³/6*logn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int countQuadruplets(vector<int>& nums) {

constexpr int kMax = 100;

const int n = nums.size();

int ans = 0;

vector<vector<int>> m(kMax + 1);

for (int i = 0; i < n; ++i)

m[nums[i]].push_back(i);

for (int a = 0; a < n; ++a)

for (int b = a + 1; b < n; ++b)

for (int c = b + 1; c < n; ++c) {

const int t = nums[a] + nums[b] + nums[c];

if (t > kMax) continue;

ans += end(m[t]) - lower_bound(begin(m[t]), end(m[t]), c + 1);

}

return ans;

}

};

Solution 3: Dynamic frequency table (29ms)

Similar to 花花酱 LeetCode 1. Two Sum, we dynamically add elements (from right to left) into the hashtable.

Time complexity: O(n³/6)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int countQuadruplets(vector<int>& nums) {

constexpr int kMax = 100;

const int n = nums.size();

int ans = 0;

vector<int> m(kMax + 1);

// for every c we had seen, we can use it as target (nums[d]).

for (int c = n - 1; c >= 0; ++m[nums[c--]])

for (int a = 0; a < c; ++a)

for (int b = a + 1; b < c; ++b) {

const int t = nums[a] + nums[b] + nums[c];

if (t > kMax) continue;

ans += m[t];

}

return ans;

}

};

花花酱 LeetCode 1300. Sum of Mutated Array Closest to Target

By zxi on December 24, 2021

Given an integer array arr and a target value target, return the integer value such that when we change all the integers larger than value in the given array to be equal to value, the sum of the array gets as close as possible (in absolute difference) to target.

In case of a tie, return the minimum such integer.

Notice that the answer is not neccesarilly a number from arr.

Example 1:

Input: arr = [4,9,3], target = 10
Output: 3
Explanation: When using 3 arr converts to [3, 3, 3] which sums 9 and that's the optimal answer.

Example 2:

Input: arr = [2,3,5], target = 10
Output: 5

Example 3:

Input: arr = [60864,25176,27249,21296,20204], target = 56803
Output: 11361

Constraints:

1 <= arr.length <= 10⁴
1 <= arr[i], target <= 10⁵

Solution: Binary Search

Find the smallest number x s.t. sum of the mutated array is >= target. Answer must be either x or x – 1.

Note, the search range should be [0, max(arr))

Time complexity: O(nlogm)
Space complexity: O(1)

C++

// Author: Huahua]

class Solution {

public:

int findBestValue(vector<int>& arr, int target) {

int l = 0;

int r = *max_element(begin(arr), end(arr));

int ans = 0;

auto sum = [&](int v) {

int ans = 0;

for (int x : arr)

ans += min(x, v);

return ans;

};

while (l < r) {

int m = l + (r - l) / 2;

if (sum(m) >= target)

r = m;

else

l = m + 1;

}

return abs(sum(l) - target) < abs(sum(l - 1) - target) ? l : l - 1;

}

};

花花酱 LeetCode 2111. Minimum Operations to Make the Array K-Increasing

By zxi on December 22, 2021

You are given a 0-indexed array arr consisting of n positive integers, and a positive integer k.

The array arr is called K-increasing if arr[i-k] <= arr[i] holds for every index i, where k <= i <= n-1.

For example, arr = [4, 1, 5, 2, 6, 2] is K-increasing for k = 2 because:
- arr[0] <= arr[2] (4 <= 5)
- arr[1] <= arr[3] (1 <= 2)
- arr[2] <= arr[4] (5 <= 6)
- arr[3] <= arr[5] (2 <= 2)
However, the same arr is not K-increasing for k = 1 (because arr[0] > arr[1]) or k = 3 (because arr[0] > arr[3]).

In one operation, you can choose an index i and change arr[i] into any positive integer.

Return the minimum number of operations required to make the array K-increasing for the given k.

Example 1:

Input: arr = [5,4,3,2,1], k = 1
Output: 4
Explanation:
For k = 1, the resultant array has to be non-decreasing.
Some of the K-increasing arrays that can be formed are [5,6,7,8,9], [1,1,1,1,1], [2,2,3,4,4]. All of them require 4 operations.
It is suboptimal to change the array to, for example, [6,7,8,9,10] because it would take 5 operations.
It can be shown that we cannot make the array K-increasing in less than 4 operations.

Example 2:

Input: arr = [4,1,5,2,6,2], k = 2
Output: 0
Explanation:
This is the same example as the one in the problem description.
Here, for every index i where 2 <= i <= 5, arr[i-2] <=arr[i].
Since the given array is already K-increasing, we do not need to perform any operations.

Example 3:

Input: arr = [4,1,5,2,6,2], k = 3
Output: 2
Explanation:
Indices 3 and 5 are the only ones not satisfying arr[i-3] <= arr[i] for 3 <= i <= 5.
One of the ways we can make the array K-increasing is by changing arr[3] to 4 and arr[5] to 5.
The array will now be [4,1,5,4,6,5].
Note that there can be other ways to make the array K-increasing, but none of them require less than 2 operations.

Constraints:

1 <= arr.length <= 10⁵
1 <= arr[i], k <= arr.length

Solution: Longest increasing subsequence

if k = 1, we need to modify the following arrays
1. [a[0], a[1], a[2], …]
if k = 2, we need to modify the following arrays
1. [a[0], a[2], a[4], …]
2. [a[1], a[3], a[5], …]
if k = 3, we need to modify the following arrays
1. [a[0], a[3], a[6], …]
2. [a[1], a[4], a[7], …]
3. [a[2], a[5], a[8], …]
…

These arrays are independent of each other, we just need to find LIS of it, # ops = len(arr) – LIS(arr).
Ans = sum(len(arr_i) – LIS(arr_i)) 1 <= i <= k

Reference: 花花酱 LeetCode 300. Longest Increasing Subsequence

Time complexity: O(k * (n/k)* log(n/k)) = O(n * log(n/k))
Space complexity: O(n/k)

C++

// Author: Huahua

class Solution {

public:

int kIncreasing(vector<int>& arr, int k) {

auto LIS = [](const vector<int>& nums) {

vector<int> lis;

for (int x : nums)

if (lis.empty() || lis.back() <= x)

lis.push_back(x);

else

*upper_bound(begin(lis), end(lis), x) = x;

return lis.size();

};

const int n = arr.size();

int ans = 0;

for (int i = 0; i < k; ++i) {

vector<int> cur;

for (int j = i; j < n; j += k)

cur.push_back(arr[j]);

ans += cur.size() - LIS(cur);

}

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def kIncreasing(self, arr: List[int], k: int) -> int:

def LIS(arr: List[int]) -> int:

lis = []

for x in arr:

if not lis or lis[-1] <= x:

lis.append(x)

else:

lis[bisect_right(lis, x)] = x

return len(lis)

return sum(len(arr[i::k]) - LIS(arr[i::k]) for i in range(k))

花花酱 LeetCode 81. Search in Rotated Sorted Array II

By zxi on November 29, 2021

There is an integer array nums sorted in non-decreasing order (not necessarily with distinct values).

Before being passed to your function, nums is rotated at an unknown pivot index k (0 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,4,4,5,6,6,7] might be rotated at pivot index 5 and become [4,5,6,6,7,0,1,2,4,4].

Given the array nums after the rotation and an integer target, return true if target is in nums, or false if it is not in nums.

You must decrease the overall operation steps as much as possible.

Example 1:

Input: nums = [2,5,6,0,0,1,2], target = 0
Output: true

Example 2:

Input: nums = [2,5,6,0,0,1,2], target = 3
Output: false

Constraints:

1 <= nums.length <= 5000
-10⁴ <= nums[i] <= 10⁴
nums is guaranteed to be rotated at some pivot.
-10⁴ <= target <= 10⁴

Solution: Binary search or divide and conquer

If current range is ordered, use binary search, Otherwise, divide and conquer.

Time complexity: O(logn) best, O(n) worst
Space complexity: O(logn)

C++

// Author: Huahua

class Solution {

public:

bool search(vector<int>& A, int target) {

return search(A, 0, A.size() - 1, target);

}

private:

bool search(vector<int>& A, int l, int r, int target) {

if (l > r) return 0;

if (l == r) return target == A[l];

int mid = l + (r - l) / 2;

if (A[l] < A[mid] && A[mid] < A[r])

return (target <= A[mid]) ? search(A, l, mid, target) : search(A, mid + 1, r, target);

else

return search(A, l, mid, target) || search(A, mid + 1, r, target);

}

};