Posts published in “Hard”

花花酱 LeetCode 321. Create Maximum Number

By zxi on November 14, 2017

Problem:

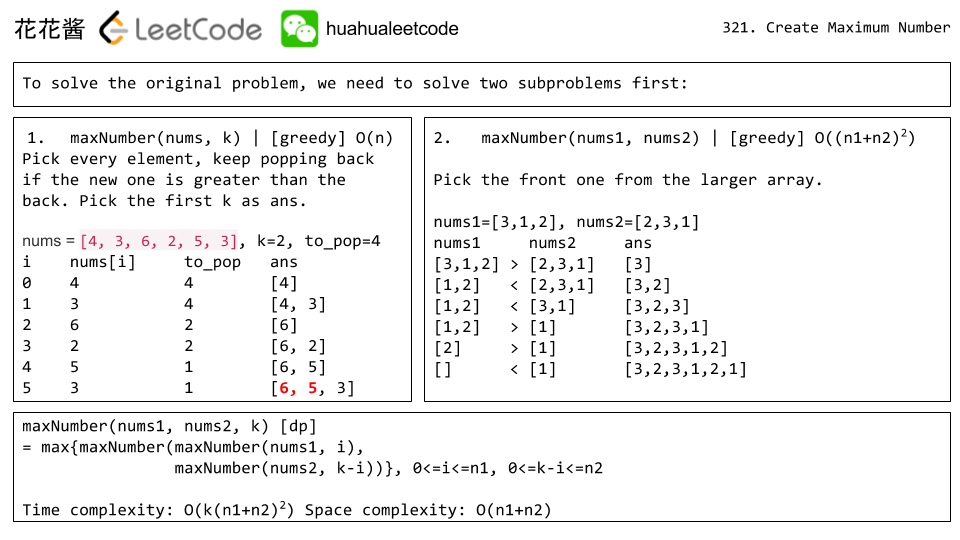
Given two arrays of length m and n with digits 0-9 representing two numbers. Create the maximum number of length k <= m + n from digits of the two. The relative order of the digits from the same array must be preserved. Return an array of the k digits. You should try to optimize your time and space complexity.

Example 1:

nums1 = [3, 4, 6, 5]
nums2 = [9, 1, 2, 5, 8, 3]
k = 5
return [9, 8, 6, 5, 3]

Example 2:

nums1 = [6, 7]
nums2 = [6, 0, 4]
k = 5
return [6, 7, 6, 0, 4]

Example 3:

nums1 = [3, 9]
nums2 = [8, 9]
k = 3
return [9, 8, 9]

题目大意：给你两个数字数组和k，返回从两个数组中选取k个数字能够组成的最大值。

Idea: Greedy + DP

Solution:

Time complexity: O(k * (n1+n2)^2)

Space complexity: O(n1+n2)

C++

// Author: Huahua

// Runtime: 26 ms

class Solution {

public:

vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {

vector<int> ans;

const int n1 = nums1.size();

const int n2 = nums2.size();

for (int i = max(0, k - n2); i <= min(k, n1); ++i)

ans = max(ans, maxNumber(maxNumber(nums1, i),

maxNumber(nums2, k - i)));

return ans;

}

private:

vector<int> maxNumber(const vector<int>& nums, int k) {

vector<int> ans(k);

int j = 0;

for (int i = 0; i < nums.size(); ++i) {

while (j > 0 && nums[i] > ans[j - 1]

&& nums.size() - i > k - j) --j;

if (j < k) ans[j++] = nums[i];

}

return ans;

}

vector<int> maxNumber(const vector<int>& nums1, const vector<int>& nums2) {

vector<int> ans(nums1.size() + nums2.size());

auto s1 = nums1.cbegin();

auto e1 = nums1.cend();

auto s2 = nums2.cbegin();

auto e2 = nums2.cend();

int index = 0;

while (s1 != e1 || s2 != e2)

ans[index++] =

lexicographical_compare(s1, e1, s2, e2) ? *s2++ : *s1++;

return ans;

}

};

Java

// Author: Huahua

// Runtime: 18 ms

class Solution {

public int[] maxNumber(int[] nums1, int[] nums2, int k) {

int[] best = new int[0];

for (int i = Math.max(0, k - nums2.length);

i <= Math.min(k, nums1.length); ++i)

best = max(best, 0,

maxNumber(maxNumber(nums1, i),

maxNumber(nums2, k - i)), 0);

return best;

}

private int[] maxNumber(int[] nums, int k) {

int[] ans = new int[k];

int j = 0;

for (int i = 0; i < nums.length; ++i) {

while (j > 0 && nums[i] > ans[j - 1]

&& nums.length - i > k - j) --j;

if (j < k)

ans[j++] = nums[i];

}

return ans;

}

private int[] maxNumber(int[] nums1, int[] nums2) {

int[] ans = new int[nums1.length + nums2.length];

int s1 = 0;

int s2 = 0;

int index = 0;

while (s1 != nums1.length || s2 != nums2.length)

ans[index++] = max(nums1, s1, nums2, s2) == nums1 ?

nums1[s1++] : nums2[s2++];

return ans;

}

private int[] max(int[] nums1, int s1, int[] nums2, int s2) {

for (int i = s1; i < nums1.length; ++i) {

int j = s2 + i - s1;

if (j >= nums2.length) return nums1;

if (nums1[i] < nums2[j]) return nums2;

if (nums1[i] > nums2[j]) return nums1;

}

return nums2;

}

花花酱 LeetCode 4. Median of Two Sorted Arrays

By zxi on November 8, 2017

题目大意：求两个已经排序的数组的中位数（如果合并后）。

Problem:

There are two sorted arrays nums1 and nums2 of size m and n respectively.

Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).

Example 1:

nums1 = [1, 3]

nums2 = [2]

The median is 2.0

Example 2:

nums1 = [1, 2]

nums2 = [3, 4]

The median is (2 + 3)/2 = 2.5

Idea:

Binary Search

Time complexity: O(log(min(n1,n2)))

Space complexity: O(1)

Solution: Binary Search

C++

// Author: Huahua

// Runtime: 52 ms

class Solution {

public:

double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {

const int n1 = nums1.size();

const int n2 = nums2.size();

// Make sure n1 <= n2

if (n1 > n2) return findMedianSortedArrays(nums2, nums1);

const int k = (n1 + n2 + 1) / 2;

int l = 0;

int r = n1;

while (l < r) {

const int m1 = l + (r - l) / 2;

const int m2 = k - m1;

if (nums1[m1] < nums2[m2 - 1])

l = m1 + 1;

else

r = m1;

}

const int m1 = l;

const int m2 = k - l;

const int c1 = max(m1 <= 0 ? INT_MIN : nums1[m1 - 1],

m2 <= 0 ? INT_MIN : nums2[m2 - 1]);

if ((n1 + n2) % 2 == 1)

return c1;

const int c2 = min(m1 >= n1 ? INT_MAX : nums1[m1],

m2 >= n2 ? INT_MAX : nums2[m2]);

return (c1 + c2) * 0.5;

}

};

Java

// Author: Huahua

// Runtime: 66 ms

class Solution {

public double findMedianSortedArrays(int[] nums1, int[] nums2) {

int n1 = nums1.length;

int n2 = nums2.length;

if (n1 > n2)

return findMedianSortedArrays(nums2, nums1);

int k = (n1 + n2 + 1) / 2;

int l = 0;

int r = n1;

while (l < r) {

int m1 = l + (r - l) / 2;

int m2 = k - m1;

if (nums1[m1] < nums2[m2 - 1])

l = m1 + 1;

else

r = m1;

}

int m1 = l;

int m2 = k - l;

int c1 = Math.max(m1 <= 0 ? Integer.MIN_VALUE : nums1[m1 - 1],

m2 <= 0 ? Integer.MIN_VALUE : nums2[m2 - 1]);

if ((n1 + n2) % 2 == 1)

return c1;

int c2 = Math.min(m1 >= n1 ? Integer.MAX_VALUE : nums1[m1],

m2 >= n2 ? Integer.MAX_VALUE : nums2[m2]);

return (c1 + c2) * 0.5;

}

Related Problem:

[解题报告] LeetCode 295. Find Median from Data Stream O(logn) + O(1)

花花酱 LeetCode 719. Find K-th Smallest Pair Distance

By zxi on October 29, 2017

题目大意：给你一个数组，返回所有数对中，绝对值差第k小的值。

Problem:

Given an integer array, return the k-th smallest distance among all the pairs. The distance of a pair (A, B) is defined as the absolute difference between A and B.

Example 1:

Input:

nums = [1,3,1]

k = 1

Output: 0

Explanation:

Here are all the pairs:

(1,3) -> 2

(1,1) -> 0

(3,1) -> 2

Then the 1st smallest distance pair is (1,1), and its distance is 0.

Note:

2 <= len(nums) <= 10000.
0 <= nums[i] < 1000000.
1 <= k <= len(nums) * (len(nums) - 1) / 2.

Idea

Bucket sort

Binary search / dp

Solution

C++ / binary search

// Author: Huahua

// Runtime: 9 ms

class Solution {

public:

int smallestDistancePair(vector<int>& nums, int k) {

std::sort(nums.begin(), nums.end());

int n = nums.size();

int l = 0;

int r = nums.back() - nums.front();

while (l <= r) {

int cnt = 0;

int j = 0;

int m = l + (r - l) / 2;

for (int i = 0; i < n; ++i) {

while (j < n && nums[j] - nums[i] <= m) ++j;

cnt += j - i - 1;

}

cnt >= k ? r = m - 1 : l = m + 1;

}

return l;

}

};

C++ / bucket sort w/ vector O(n^2)

// Author: Huahua

// Runtime: 549 ms

class Solution {

public:

int smallestDistancePair(vector<int>& nums, int k) {

std::sort(nums.begin(), nums.end());

const int N = nums.back();

vector<int> count(N + 1, 0);

const int n = nums.size();

for (int i = 0; i < n; ++i)

for (int j = i + 1; j < n; ++j)

++count[nums[j] - nums[i]];

for (int i = 0; i <= N; ++i) {

k -= count[i];

if (k <= 0) return i;

}

return 0;

}

};

Related Problems:

花花酱 LeetCode 699. Falling Squares

By zxi on October 24, 2017

题目大意：方块落下后会堆叠在重叠的方块之上，问每一块方块落下之后最高的方块的高度是多少？

Problem:

On an infinite number line (x-axis), we drop given squares in the order they are given.

The i-th square dropped (positions[i] = (left, side_length)) is a square with the left-most point being positions[i][0] and sidelength positions[i][1].

The square is dropped with the bottom edge parallel to the number line, and from a higher height than all currently landed squares. We wait for each square to stick before dropping the next.

The squares are infinitely sticky on their bottom edge, and will remain fixed to any positive length surface they touch (either the number line or another square). Squares dropped adjacent to each other will not stick together prematurely.

Return a list ans of heights. Each height ans[i] represents the current highest height of any square we have dropped, after dropping squares represented by positions[0], positions[1], ..., positions[i].

Example 1:

Input: [[1, 2], [2, 3], [6, 1]]

Output: [2, 5, 5]

Explanation:

After the first drop of

positions[0] = [1, 2]:

_aa

-------

The maximum height of any square is 2.

After the second drop of

positions[1] = [2, 3]:

__aaa

_aa__

--------------

The maximum height of any square is 5.

The larger square stays on top of the smaller square despite where its center

of gravity is, because squares are infinitely sticky on their bottom edge.

After the third drop of

positions[1] = [6, 1]:

__aaa

_aa

_aa___a

--------------

The maximum height of any square is still 5.

Thus, we return an answer of

[2, 5, 5]

Example 2:

Input: [[100, 100], [200, 100]]

Output: [100, 100]

Explanation: Adjacent squares don't get stuck prematurely - only their bottom edge can stick to surfaces.

Note:

1 <= positions.length <= 1000.
1 <= positions[i][0] <= 10^8.
1 <= positions[i][1] <= 10^6.

Idea:

Range query with map

Solution:

C++ map

// Author: Huahua

// Runtime: 29 ms

class Solution {

public:

vector<int> fallingSquares(vector<pair<int, int>>& positions) {

vector<int> ans;

map<pair<int, int>, int> b; // {{start, end}, height}

int maxHeight = INT_MIN;

for (const auto& kv: positions) {

int start = kv.first;

int size = kv.second;

int end = start + size;

// first range intersect with new_interval

auto it = b.upper_bound({start, end});

if (it != b.begin()) {

auto it2 = it;

if ((--it2)->first.second > start) it = it2;

}

int baseHeight = 0;

vector<tuple<int, int, int>> ranges;

while (it != b.end() && it->first.first < end) {

const int s = it->first.first;

const int e = it->first.second;

const int h = it->second;

if (s < start) ranges.emplace_back(s, start, h);

if (e > end) ranges.emplace_back(end, e, h);

// max height of intesected ranges

baseHeight = max(baseHeight, h);

it = b.erase(it);

}

int newHeight = size + baseHeight;

b[{start, end}] = newHeight;

for (const auto& range: ranges)

b[{get<0>(range), get<1>(range)}] = get<2>(range);

maxHeight = max(maxHeight, newHeight);

ans.push_back(maxHeight);

}

return ans;

}

};

C++ vector without merge

// Author: Huahua

// Runtime: 46 ms

class Solution {

public:

vector<int> fallingSquares(vector<pair<int, int>>& positions) {

vector<int> ans;

vector<Interval> intervals;

int maxHeight = INT_MIN;

for (const auto& kv: positions) {

int start = kv.first;

int end = start + kv.second;

int baseHeight = 0;

for (const Interval& interval : intervals) {

if (interval.start >= end || interval.end <= start)

continue;

baseHeight = max(baseHeight, interval.height);

}

int height = kv.second + baseHeight;

intervals.push_back(Interval(start, end, height));

maxHeight = max(maxHeight, height);

ans.push_back(maxHeight);

}

return ans;

}

private:

struct Interval {

int start;

int end;

int height;

Interval(int start, int end, int height)

: start(start), end(end), height(height) {}

};

C++ / vector with merge (slower)

// Author: Huahua

// Runtime: 86 ms

class Solution {

public:

vector<int> fallingSquares(vector<pair<int, int>>& positions) {

vector<int> ans;

vector<Interval> intervals;

int maxHeight = INT_MIN;

for (const auto& kv: positions) {

vector<Interval> tmp;

int start = kv.first;

int end = start + kv.second;

int baseHeight = 0;

for (const Interval& interval : intervals) {

if (interval.start >= end || interval.end <= start) {

tmp.push_back(interval);

continue;

}

baseHeight = max(baseHeight, interval.height);

if (interval.start < start || interval.end > end)

tmp.push_back(interval);

}

int height = kv.second + baseHeight;

tmp.push_back(Interval(start, end, height));

intervals.swap(tmp);

maxHeight = max(maxHeight, height);

ans.push_back(maxHeight);

}

return ans;

}

private:

struct Interval {

int start;

int end;

int height;

Interval(int start, int end, int height)

: start(start), end(end), height(height) {}

};

Related Problems:

[解题报告] LeetCode 715. Range Module
[解题报告] LeetCode 218. The Skyline Problem
[解题报告] LeetCode 57. Insert Interval

花花酱 LeetCode 715. Range Module

By zxi on October 22, 2017

Problem:

A Range Module is a module that tracks ranges of numbers. Your task is to design and implement the following interfaces in an efficient manner.

addRange(int left, int right) Adds the half-open interval [left, right), tracking every real number in that interval. Adding an interval that partially overlaps with currently tracked numbers should add any numbers in the interval [left, right) that are not already tracked.
queryRange(int left, int right) Returns true if and only if every real number in the interval [left, right) is currently being tracked.
removeRange(int left, int right) Stops tracking every real number currently being tracked in the interval [left, right).

Example 1:

addRange(10, 20): null

removeRange(14, 16): null

queryRange(10, 14): true (Every number in [10, 14) is being tracked)

queryRange(13, 15): false (Numbers like 14, 14.03, 14.17 in [13, 15) are not being tracked)

queryRange(16, 17): true (The number 16 in [16, 17) is still being tracked, despite the remove operation)

Note:

A half open interval [left, right) denotes all real numbers left <= x < right.
0 < left < right < 10^9 in all calls to addRange, queryRange, removeRange.
The total number of calls to addRange in a single test case is at most 1000.
The total number of calls to queryRange in a single test case is at most 5000.
The total number of calls to removeRange in a single test case is at most 1000.

Idea:

map / ordered ranges

Solution:

C++ / vector

// Author: Huahua

// Runtime: 276 ms

class RangeModule {

public:

RangeModule() {}

void addRange(int left, int right) {

vector<pair<int, int>> new_ranges;

bool inserted = false;

for (const auto& kv : ranges_) {

if (kv.first > right && !inserted) {

new_ranges.emplace_back(left, right);

inserted = true;

}

if (kv.second < left || kv.first > right) {

new_ranges.push_back(kv);

} else {

left = min(left, kv.first);

right = max(right, kv.second);

}

if (!inserted) new_ranges.emplace_back(left, right);

ranges_.swap(new_ranges);

}

bool queryRange(int left, int right) {

const int n = ranges_.size();

int l = 0;

int r = n - 1;

// Binary search

while (l <= r) {

int m = l + (r - l) / 2;

if (ranges_[m].second < left)

l = m + 1;

else if (ranges_[m].first > right)

r = m - 1;

else

return ranges_[m].first <= left && ranges_[m].second >= right;

}

return false;

}

void removeRange(int left, int right) {

vector<pair<int, int>> new_ranges;

for (const auto& kv : ranges_) {

if (kv.second <= left || kv.first >= right) {

new_ranges.push_back(kv);

} else {

if (kv.first < left)

new_ranges.emplace_back(kv.first, left);

if (kv.second > right)

new_ranges.emplace_back(right, kv.second);

}

ranges_.swap(new_ranges);

}

vector<pair<int, int>> ranges_;

};

C++ / map

// Author: Huahua

// Runtime: 199 ms

class RangeModule {

public:

RangeModule() {}

void addRange(int left, int right) {

IT l, r;

getOverlapRanges(left, right, l, r);

// At least one range overlapping with [left, right)

if (l != r) {

// Merge intervals into [left, right)

auto last = r; --last;

left = min(left, l->first);

right = max(right, last->second);

// Remove all overlapped ranges

ranges_.erase(l, r);

}

// Add a new/merged range

ranges_[left] = right;

}

bool queryRange(int left, int right) {

IT l, r;

getOverlapRanges(left, right, l, r);

// No overlapping range

if (l == r) return false;

return l->first <= left && l->second >= right;

}

void removeRange(int left, int right) {

IT l, r;

getOverlapRanges(left, right, l, r);

// No overlapping range

if (l == r) return;

auto last = r; --last;

int start = min(left, l->first);

int end = max(right, last->second);

// Delete overlapping ranges

ranges_.erase(l, r);

if (start < left) ranges_[start] = left;

if (end > right) ranges_[right] = end;

}

private:

typedef map<int, int>::iterator IT;

map<int, int> ranges_;

void getOverlapRanges(int left, int right, IT& l, IT& r) {

l = ranges_.upper_bound(left);

r = ranges_.upper_bound(right);

if (l != ranges_.begin())

if ((--l)->second < left) l++;

}

};

Related Problems: