Posts published in “Dynamic Programming”

花花酱 LeetCode 960. Delete Columns to Make Sorted III

By zxi on December 19, 2018

We are given an array A of N lowercase letter strings, all of the same length.

Now, we may choose any set of deletion indices, and for each string, we delete all the characters in those indices.

For example, if we have an array A = ["babca","bbazb"] and deletion indices {0, 1, 4}, then the final array after deletions is ["bc","az"].

Suppose we chose a set of deletion indices D such that after deletions, the final array has every element (row) in lexicographic order.

For clarity, A[0] is in lexicographic order (ie. A[0][0] <= A[0][1] <= ... <= A[0][A[0].length - 1]), A[1] is in lexicographic order (ie. A[1][0] <= A[1][1] <= ... <= A[1][A[1].length - 1]), and so on.

Return the minimum possible value of D.length.

Example 1:

Input: ["babca","bbazb"]
Output: 3
Explanation: After deleting columns 0, 1, and 4, the final array is A = ["bc", "az"].
Both these rows are individually in lexicographic order (ie. A[0][0] <= A[0][1] and A[1][0] <= A[1][1]).
Note that A[0] > A[1] - the array A isn't necessarily in lexicographic order.

Example 2:

Input: ["edcba"]
Output: 4
Explanation: If we delete less than 4 columns, the only row won't be lexicographically sorted.

Example 3:

Input: ["ghi","def","abc"]
Output: 0
Explanation: All rows are already lexicographically sorted.

Note:

1 <= A.length <= 100
1 <= A[i].length <= 100

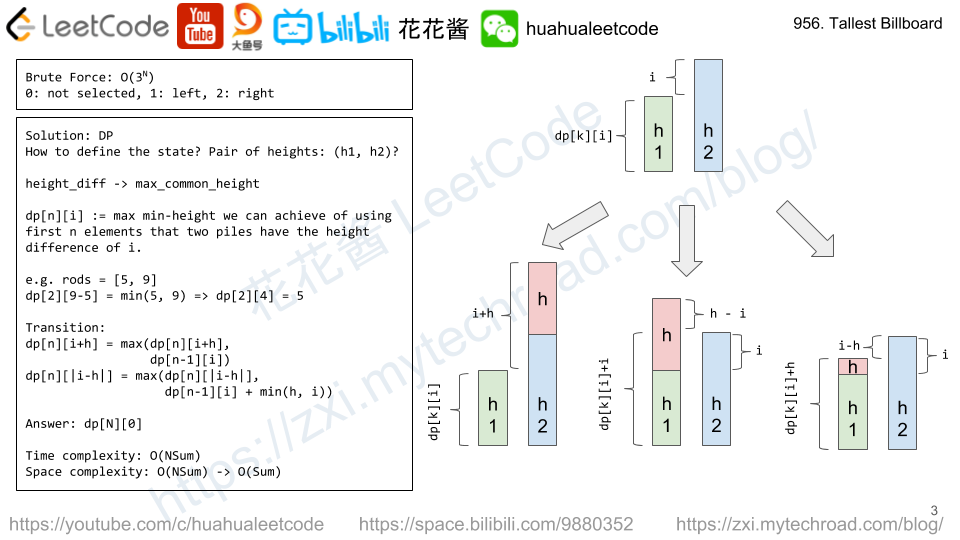
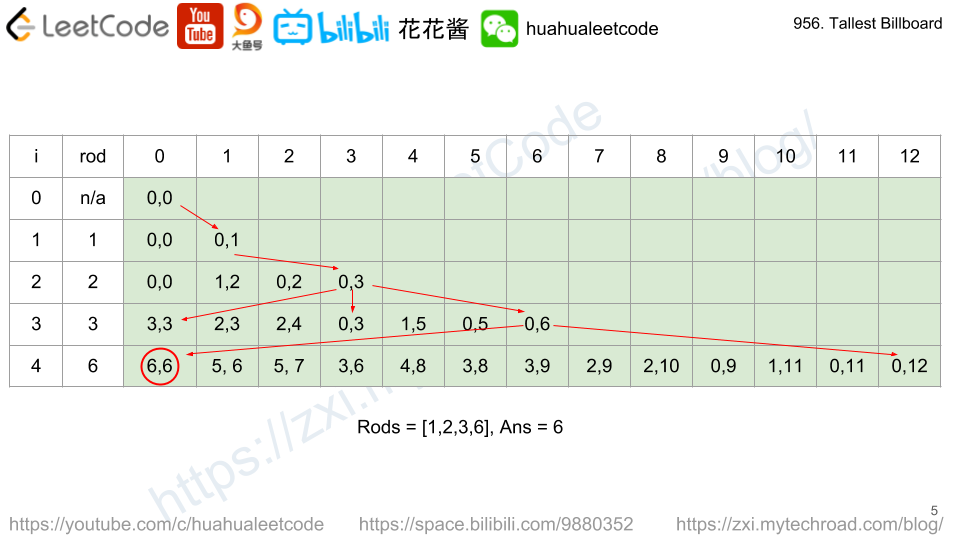
Solution: DP

dp[i] := max length of increasing sub-sequence (of all strings) ends with i-th letter.
dp[i] = max(dp[j] + 1) if all A[*][j] <= A[*][i], j < i
Time complexity: (n*L^2)
Space complexity: O(L)

C++

// Author: Huahua, running time: 24 ms

class Solution {

public:

int minDeletionSize(vector<string>& A) {

vector<int> dp(A[0].length(), 1);

for (int i = 0; i < A[0].length(); ++i)

for (int j = 0; j < i; ++j) {

bool valid = true;

for (const auto& a : A)

if (a[j] > a[i]) {

valid = false;

break;

}

if (valid) dp[i] = max(dp[i], dp[j] + 1);

}

return A[0].length() - *max_element(begin(dp), end(dp));

}

};

Python3

// Author: Huahua, running time: 176 ms

class Solution:

def minDeletionSize(self, A):

n = len(A[0])

dp = [1] * n

for i in range(1, n):

for j in range(i):

valid = True

for a in A:

if a[j] > a[i]:

valid = False

break

if valid:

dp[i] = max(dp[i], dp[j] + 1)

return n - max(dp)

花花酱 LeetCode 956. Tallest Billboard

By zxi on December 9, 2018

Problem

You are installing a billboard and want it to have the largest height. The billboard will have two steel supports, one on each side. Each steel support must be an equal height.

You have a collection of rods which can be welded together. For example, if you have rods of lengths 1, 2, and 3, you can weld them together to make a support of length 6.

Return the largest possible height of your billboard installation. If you cannot support the billboard, return 0.

Example 1:

Input: [1,2,3,6]
Output: 6
Explanation: We have two disjoint subsets {1,2,3} and {6}, which have the same sum = 6.

Example 2:

Input: [1,2,3,4,5,6]
Output: 10
Explanation: We have two disjoint subsets {2,3,5} and {4,6}, which have the same sum = 10.

Example 3:

Input: [1,2]
Output: 0
Explanation: The billboard cannot be supported, so we return 0.

Note:

0 <= rods.length <= 20
1 <= rods[i] <= 1000
The sum of rods is at most 5000.

Solution: DP

如果直接暴力搜索的话时间复杂度是O(3^N)，铁定超时。对于每一根我们可以选择1、放到左边，2、放到右边，3、不使用。最后再看一下左边和右边是否相同。

题目的数据规模中的这句话非常重要：

The sum of rods is at most 5000.

这句话就是告诉你算法的时间复杂度和sum of rods有关系，通常需要使用DP。

由于每根柱子只能使用一次（让我们想到了回复 01背包），但是我们怎么去描述放到左边还是放到右边呢？

Naive的方法是用 dp[i] 表示使用前i个柱子能够构成的柱子高度的集合。

e.g. dp[i] = {(h1, h2)}, h1 <= h2

和暴力搜索比起来DP已经对状态进行了压缩，因为我并不需要关心h1, h2是通过哪些（在我之前的）柱子构成了，我只关心它们的当前高度。

然后我可以选择

1、不用第i根柱子

2、放到低的那一堆

3、放到高的那一堆

状态转移的伪代码：

for h1, h2 in dp[i – 1]:

dp[i] += (h1, h2) # not used

dp[i] += (h1, h2 + h) # put on higher

if h1 + h < h2:

dp[i] += (h1 + h, h2) # put on lower

else:

dp[i] += (h2, h1 + h) # put on lower

假设 rods=[1,1,2]

dp[0] = {(0,0)}

dp[1] = {(0,0), (0,1)}

dp[2] = {(0,0), (0,1), (0,2), (1,1)}

dp[3] = {(0,0), (0,1), (0,2), (0,3), (0,4), (1,1), (1,2), (1,3), (2,2)}

但是dp[i]这个集合的大小可能达到sum^2，所以还是会超时…

时间复杂度 O(n*sum^2)

空间复杂度 O(n*sum^2) 可降维至 O(sum^2)

革命尚未成功，同志仍需努力!

all pairs的cost太大，我们还需要继续压缩状态！

重点来了

通过观察发现，若有2个pairs：

(h1, h2), (h3, h4),

h1 <= h2, h3 <= h4, h1 < h3, h2 – h1 = h4 – h3 即 高度差 相同

如果 min(h1, h2) < min(h3, h4) 那么(h1, h2) 不可能产生最优解，直接舍弃。

因为如果后面的柱子可以构成 h4 – h3/h2 – h1 填补高度差，使得两根柱子一样高，那么答案就是 h2 和 h4。但h2 < h4，所以最优解只能来自后者。

举个例子：我有 (1, 3) 和 (2, 4) 两个pairs，它们的高度差都是2，假设我还有一个长度为2的柱子，那么我可以构成(1+2, 3) 以及 (2+2, 4)，虽然这两个都是解。但是后者的高度要大于前者，所以前者无法构成最优解，也就没必要存下来。

所以，我们可以把状态压缩到高度差，对于相同的高度差，我只存h1最大的。

我们用 dp[i][j] 来表示使用前i个柱子，高度差为j的情况下最大的公共高度h1是多少。

状态转移（如下图）

dp[i][j] = max(dp[i][j], dp[i – 1][j])

dp[i][j+h] = max(dp[i][j + h], dp[i – 1][j])

dp[i][|j-h|] = max(dp[i][|j-h|], dp[i – 1][j] + min(j, h))

时间复杂度 O(nsum)

空间复杂度 O(nsum) 可降维至 O(sum)

dp[i] := max common height of two piles of height difference i.

e.g. y1 = 5, y2 = 9 => dp[9 – 5] = min(5, 9) => dp[4] = 5.

answer: dp[0]

Time complexity: O(n*Sum)

Space complexity: O(Sum)

C++ hashmap

// Author: Huahua, 172 ms

class Solution {

public:

int tallestBillboard(vector<int>& rods) {

unordered_map<int, int> dp;

dp[0] = 0;

for (int rod : rods) {

auto cur = dp;

for (const auto& kv : cur) {

const int k = kv.first;

dp[k + rod] = max(dp[k + rod], cur[k]);

dp[abs(k - rod)] = max(dp[abs(k - rod)], cur[k] + min(rod, k));

}

return dp[0];

}

};

C++ / array

// Author: Huahua, 8 ms

class Solution {

public:

int tallestBillboard(vector<int>& rods) {

const int s = accumulate(begin(rods), end(rods), 0);

vector<int> dp(s + 1, -1);

dp[0] = 0;

for (int rod : rods) {

vector<int> cur(dp);

for (int i = 0; i <= s - rod; ++i) {

if (cur[i] < 0) continue;

dp[i + rod] = max(dp[i + rod], cur[i]);

dp[abs(i - rod)] = max(dp[abs(i - rod)], cur[i] + min(rod, i));

}

return dp[0];

}

};

C++/2D array

// Author: Huahua, 12 ms

class Solution {

public:

int tallestBillboard(vector<int>& rods) {

const int n = rods.size();

const int s = accumulate(begin(rods), end(rods), 0);

// dp[i][j] := min(h1, h2), j = abs(h1 - h2)

vector<vector<int>> dp(n + 1, vector<int>(s + 1, -1));

dp[0][0] = 0;

for (int i = 1; i <= n; ++i) {

int h = rods[i - 1];

for (int j = 0; j <= s - h; ++j) {

if (dp[i - 1][j] < 0) continue;

// not used

dp[i][j] = max(dp[i][j], dp[i - 1][j]);

// put on the taller one

dp[i][j + h] = max(dp[i][j + h], dp[i - 1][j]);

// put on the shorter one

dp[i][abs(j - h)] = max(dp[i][abs(j - h)], dp[i - 1][j] + min(h, j));

}

return dp[n][0];

}

};

花花酱 LeetCode 940. Distinct Subsequences II

By zxi on November 14, 2018

Problem

Given a string S, count the number of distinct, non-empty subsequences of S .

Since the result may be large, return the answer modulo 10^9 + 7.

Example 1:

Input: "abc"
Output: 7
Explanation: The 7 distinct subsequences are "a", "b", "c", "ab", "ac", "bc", and "abc".

Example 2:

Input: "aba"
Output: 6
Explanation: The 6 distinct subsequences are "a", "b", "ab", "ba", "aa" and "aba".

Example 3:

Input: "aaa"
Output: 3
Explanation: The 3 distinct subsequences are "a", "aa" and "aaa".

Note:

S contains only lowercase letters.
1 <= S.length <= 2000

Solution: DP

counts[i][j] := # of distinct sub sequences of s[1->i] and ends with letter j. (‘a'<= j <= ‘z’)

Initialization:

counts[*][*] = 0

Transition:

counts[i][j] = sum(counts[i-1]) + 1 if s[i] == j else counts[i-1][j]

ans = sum(counts[n])

e.g. S = “abc”

counts[1] = {‘a’ : 1}
counts[2] = {‘a’ : 1, ‘b’ : 1 + 1 = 2}
counts[3] = {‘a’ : 1, ‘b’ : 2, ‘c’: 1 + 2 + 1 = 4}
ans = sum(counts[3]) = 1 + 2 + 4 = 7

Time complexity: O(N*26)

Space complexity: O(N*26) -> O(26)

C++

// Author: Huahua, running time: 12 ms

class Solution {

public:

int distinctSubseqII(string S) {

constexpr int kMod = 1e9 + 7;

std::vector<int> counts(26);

for (char c : S)

counts[c - 'a'] = accumulate(begin(counts), end(counts), 1L) % kMod;

return accumulate(begin(counts), end(counts), 0L) % kMod;

}

};

Python3

# Author: Huahua, running time: 64 ms

class Solution:

def distinctSubseqII(self, S):

kMod = 10**9 + 7

dp = {}

for c in S:

dp[c] = (sum(dp.values()) + 1) % kMod

return sum(dp.values()) % kMod

Knapsack Problem 背包问题

By zxi on November 10, 2018

Videos

上期节目中我们对动态规划做了一个总结，这期节目我们来聊聊背包问题。

背包问题是一个NP-complete的组合优化问题，Search的方法需要O(2^N)时间才能获得最优解。而使用动态规划，我们可以在伪多项式（pseudo-polynomial time）时间内获得最优解。

0-1 Knapsack Problem 0-1背包问题

Problem

Given N items, w[i] is the weight of the i-th item and v[i] is value of the i-th item. Given a knapsack with capacity W. Maximize the total value. Each item can be use 0 or 1 time.

0-1背包问题的通常定义是：一共有N件物品，第i件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够获得的最大价值是多少？每件物品可以使用0次或者1次。

例子：

重量 w = [1, 1, 2, 2]

价值 v = [1, 3, 4, 5]

背包承重 W = 4

最大价值为9，可以选第1,2,4件物品，也可以选第3，4件物品；总重量为4，总价值为9。

动态规划的状态转移方程为：

1	dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]] + v[i])

Solutions

Search

def knapsack01DFS(w, v, W):

def dfs(s, cur_w, cur_v, ans):

ans[0] = max(ans[0], cur_v)

if s == N: return

for i in range(s, N):

if cur_w + w[i] <= W:

dfs(i + 1, cur_w + w[i], cur_v + v[i], ans)

ans = [0]

dfs(0, 0, 0, ans)

return ans[0]

DP2

def knapsack01(w, v, W):

dp = [[0] * (W + 1) for _ in range(N+1)]

for i in range(1, N + 1):

dp[i] = dp[i-1].clone()

for j in range(w[i], W + 1):

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1])

return max(dp[N])

DP1/tmp

def knapsack01R(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

tmp = list(dp)

for j in range(w[i], W + 1):

tmp[j] = max(tmp[j], dp[j - w[i]] + v[i])

dp = tmp

return max(dp)

DP1/push

def knapsack01R2(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

for j in range(W, w[i] - 1, -1):

dp[j] = max(dp[j], dp[j - w[i]] + v[i])

return max(dp)

DP1/pull

def knapsack01R1(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

for j in range(W - w[i], -1, -1):

dp[j + w[i]] = max(dp[j + w[i]], dp[j] + v[i])

return max(dp)

Unbounded Knapsack Problem 完全背包

完全背包、多重背包是常见的变形。和01背包的区别在于，完全背包每件物品可以使用无限多次，而多重背包每件物品最多可以使用n[i]次。两个问题都可以转换成01背包问题进行求解。

但是Naive的转换会大大增加时间复杂度：

完全背包：“复制”第i件物品到一共有 W/w[i] 件

多重背包：“复制”第i件物品到一共有 n[i] 件

然后直接调用01背包进行求解。

时间复杂度：

完全背包 O(Σ(W/w[i])*W)

多重背包 O(Σn[i]*W)

不难看出时间复杂度 = O(物品数量*背包承重)

背包承重是给定的，要降低运行时候，只有减少物品数量。但怎样才能减少总的物品数量呢？

这就涉及到二进制思想：任何一个正整数都可以用 (1, 2, 4, …, 2^K)的组合来表示。例如14 = 2 + 4 + 8。
原本需要放入14件相同的物品，现在只需要放入3件（重量和价值是原物品的2倍，4倍，8倍）。大幅降低了总的物品数量从而降低运行时间。

完全背包：对于第i件物品，我们只需要创建k = log(W/w[i])件虚拟物品即可。

每件虚拟物品的重量和价值为：1*(w[i], v[i]), 2*(w[i], v[i]), …, 2^k*(w[i], v[i])。

多重背包：对于第i件物品，我们只需要创建k + 1件虚拟物品即可，其中k = log(n[i])。

每件虚拟物品的重量和价值为：1*(w[i], v[i]), 2*(w[i], v[i]), …, 2^(k-1)*(w[i], v[i]), 以及 (n[i] – 2^k – 1) * (w[i], v[i])。

例如：n[i] = 14, k = 3, 虚拟物品的倍数为 1, 2, 4 和 7，这4个数组合可以组成1 ~ 14中的任何一个数，并且不会>14，即不超过n[i]。

二进制转换后直接调用01背包即可

时间复杂度：

完全背包 O(Σlog(W/w[i])*W)

多重背包 O(Σlog(n[i])*W)

空间复杂度 O(W)

其实完全背包和多重背包都可以在 O(NW)时间内完成，前者在视频中有讲到，后者属于超纲内容，以后有机会再和大家深入分享。

Bounded Knapsack Problem 多重背包

花花酱 LeetCode 935. Knight Dialer

By zxi on November 4, 2018

Problem

https://leetcode.com/problems/knight-dialer/description/

A chess knight can move as indicated in the chess diagram below:

This time, we place our chess knight on any numbered key of a phone pad (indicated above), and the knight makes N-1 hops. Each hop must be from one key to another numbered key.

Each time it lands on a key (including the initial placement of the knight), it presses the number of that key, pressing N digits total.

How many distinct numbers can you dial in this manner?

Since the answer may be large, output the answer modulo 10^9 + 7.

Example 1:

Input: 1
Output: 10

Example 2:

Input: 2
Output: 20

Example 3:

Input: 3
Output: 46

Note:

1 <= N <= 5000

Solution: DP

V1

We can define dp[k][i][j] as # of ways to dial and the last key is (j, i) after k steps

Note: dp[*][3][0], dp[*][3][2] are always zero for all the steps.

Init: dp[0][i][j] = 1

Transition: dp[k][i][j] = sum(dp[k – 1][i + dy][j + dx]) 8 ways of move from last step.

ans = sum(dp[k])

Time complexity: O(kmn) or O(k * 12 * 8) = O(k)

Space complexity: O(kmn) -> O(mn) or O(12*8) = O(1)

V2

define dp[k][i] as # of ways to dial and the last key is i after k steps

init: dp[0][0:10] = 1

transition: dp[k][i] = sum(dp[k-1][j]) that j can move to i

ans: sum(dp[k])

Time complexity: O(k * 10) = O(k)

Space complexity: O(k * 10) -> O(10) = O(1)

C++ V1

// Author: Huahua, 96 ms

class Solution {

public:

int knightDialer(int N) {

constexpr int kMod = 1e9 + 7;

int dirs[8][2] = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};

vector<vector<int>> dp(4, vector<int>(3, 1));

dp[3][0] = dp[3][2] = 0;

for (int k = 1; k < N; ++k) {

vector<vector<int>> tmp(4, vector<int>(3));

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 3; ++j) {

if (i == 3 && j != 1) continue;

for (int d = 0; d < 8; ++d) {

int tx = j + dirs[d][0];

int ty = i + dirs[d][1];

if (tx < 0 || ty < 0 || tx >= 3 || ty >= 4) continue;

tmp[i][j] = (tmp[i][j] + dp[ty][tx]) % kMod;

}

dp.swap(tmp);

}

int ans = 0;

for (int i = 0; i < 4; ++i)

for (int j = 0; j < 3; ++j)

ans = (ans + dp[i][j]) % kMod;

return ans;

}

};

C++ V2

// Author: Huahua, 24 ms

public:

int knightDialer(int N) {

constexpr int kMod = 1e9 + 7;

vector<vector<int>> moves{{4,6},{8,6},{7,9},{4,8},{3,9,0},{},{1,7,0},{2,6},{1,3},{2,4}};

vector<int> dp(10, 1);

for (int k = 1; k < N; ++k) {

vector<int> tmp(10);

for (int i = 0; i < 10; ++i)

for (int nxt : moves[i])

tmp[nxt] = (tmp[nxt] + dp[i]) % kMod;

dp.swap(tmp);

}

int ans = 0;

for (int i = 0; i < 10; ++i)

ans = (ans + dp[i]) % kMod;

return ans;

}

};

Posts published in “Dynamic Programming”

花花酱 LeetCode 960. Delete Columns to Make Sorted III

Solution: DP

C++

Python3

花花酱 LeetCode 956. Tallest Billboard

Problem

Solution: DP

C++ hashmap

C++ / array

C++/2D array

花花酱 LeetCode 940. Distinct Subsequences II

Problem

Solution: DP

C++

Python3

Knapsack Problem 背包问题

Videos

0-1 Knapsack Problem 0-1背包问题

Problem

Solutions

Search

DP2

DP1/tmp

DP1/push

DP1/pull

Unbounded Knapsack Problem 完全背包

Bounded Knapsack Problem 多重背包

花花酱 LeetCode 935. Knight Dialer

Problem

Solution: DP

V1

V2

C++ V1

C++ V2

Related Problem