Posts published in “Geometry”

花花酱 LeetCode 1779. Find Nearest Point That Has the Same X or Y Coordinate

By zxi on March 6, 2021

You are given two integers, x and y, which represent your current location on a Cartesian grid: (x, y). You are also given an array points where each points[i] = [a_i, b_i] represents that a point exists at (a_i, b_i). A point is valid if it shares the same x-coordinate or the same y-coordinate as your location.

Return the index (0-indexed) of the valid point with the smallest Manhattan distance from your current location. If there are multiple, return the valid point with the smallest index. If there are no valid points, return -1.

The Manhattan distance between two points (x₁, y₁) and (x₂, y₂) is abs(x₁ - x₂) + abs(y₁ - y₂).

Example 1:

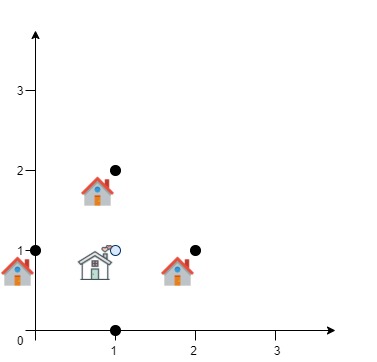
Input: x = 3, y = 4, points = [[1,2],[3,1],[2,4],[2,3],[4,4]]
Output: 2
Explanation: Of all the points, only [3,1], [2,4] and [4,4] are valid. Of the valid points, [2,4] and [4,4] have the smallest Manhattan distance from your current location, with a distance of 1. [2,4] has the smallest index, so return 2.

Example 2:

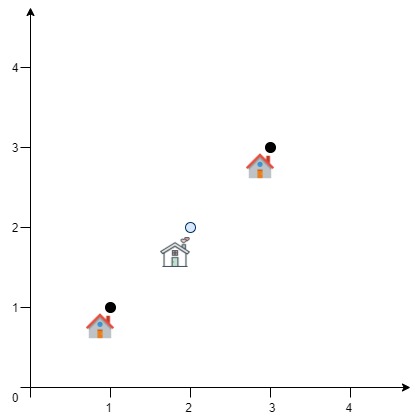
Input: x = 3, y = 4, points = [[3,4]]
Output: 0
Explanation: The answer is allowed to be on the same location as your current location.

Example 3:

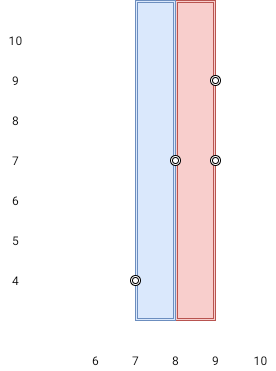
Input: x = 3, y = 4, points = [[2,3]]
Output: -1
Explanation: There are no valid points.

Constraints:

1 <= points.length <= 10⁴
points[i].length == 2
1 <= x, y, a_i, b_i <= 10⁴

Solution: Brute Force

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int nearestValidPoint(int x, int y, vector<vector<int>>& points) {

int min_dist = INT_MAX;

int ans = -1;

for (int i = 0; i < points.size(); ++i) {

const int dx = abs(points[i][0] - x);

const int dy = abs(points[i][1] - y);

if (dx * dy == 0 && dx + dy < min_dist) {

min_dist = dx + dy;

ans = i;

}

return ans;

}

};

花花酱 LeetCode 1739. Building Boxes

By zxi on January 23, 2021

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

You can place the boxes anywhere on the floor.
If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return the minimum possible number of boxes touching the floor.

Example 1:

Input: n = 3
Output: 3
Explanation: The figure above is for the placement of the three boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 2:

Input: n = 4
Output: 3
Explanation: The figure above is for the placement of the four boxes.
These boxes are placed in the corner of the room, where the corner is on the left side.

Example 3:

Input: n = 10
Output: 6
Explanation: The figure above is for the placement of the ten boxes.
These boxes are placed in the corner of the room, where the corner is on the back side.

Constraints:

1 <= n <= 10⁹

Solution: Geometry

Step 1: Build a largest pyramid that has less then n cubes, whose base area is d*(d+1) / 2
Step 2: Build a largest triangle with cubes left, whose base area is l, l*(l + 1) / 2 >= left

Time complexity: O(n^(1/3))
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int minimumBoxes(int n) {

int d = 0;

int l = 0;

while (n - (d + 1) * (d + 2) / 2 > 0) {

n -= (d + 1) * (d + 2) / 2;

++d;

}

while (n > 0) n -= ++l;

return d * (d + 1) / 2 + l;

}

};

花花酱 LeetCode 1725. Number Of Rectangles That Can Form The Largest Square

By zxi on January 17, 2021

You are given an array rectangles where rectangles[i] = [l_i, w_i] represents the i^th rectangle of length l_i and width w_i.

You can cut the i^th rectangle to form a square with a side length of k if both k <= l_i and k <= w_i. For example, if you have a rectangle [4,6], you can cut it to get a square with a side length of at most 4.

Let maxLen be the side length of the largest square you can obtain from any of the given rectangles.

Return the number of rectangles that can make a square with a side length of maxLen.

Example 1:

Input: rectangles = [[5,8],[3,9],[5,12],[16,5]]
Output: 3
Explanation: The largest squares you can get from each rectangle are of lengths [5,3,5,5].
The largest possible square is of length 5, and you can get it out of 3 rectangles.

Example 2:

Input: rectangles = [[2,3],[3,7],[4,3],[3,7]]
Output: 3

Constraints:

1 <= rectangles.length <= 1000
rectangles[i].length == 2
1 <= l_i, w_i <= 10⁹
l_i != w_i

Solution: Running Max of Shortest Edge

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countGoodRectangles(vector<vector<int>>& rectangles) {

int cur = 0;

int ans = 0;

for (const auto& r : rectangles) {

if (min(r[0], r[1]) > cur) {

cur = min(r[0], r[1]);

ans = 0;

}

if (min(r[0], r[1]) == cur) ++ans;

}

return ans;

}

};

花花酱 LeetCode 1515. Best Position for a Service Centre

By zxi on November 30, 2020

A delivery company wants to build a new service centre in a new city. The company knows the positions of all the customers in this city on a 2D-Map and wants to build the new centre in a position such that the sum of the euclidean distances to all customers is minimum.

Given an array positions where positions[i] = [x_i, y_i] is the position of the ith customer on the map, return the minimum sum of the euclidean distances to all customers.

In other words, you need to choose the position of the service centre [x_centre, y_centre] such that the following formula is minimized:

Answers within 10^-5 of the actual value will be accepted.

Example 1:

Input: positions = [[0,1],[1,0],[1,2],[2,1]]
Output: 4.00000
Explanation: As shown, you can see that choosing [x_centre, y_centre] = [1, 1] will make the distance to each customer = 1, the sum of all distances is 4 which is the minimum possible we can achieve.

Example 2:

Input: positions = [[1,1],[3,3]]
Output: 2.82843
Explanation: The minimum possible sum of distances = sqrt(2) + sqrt(2) = 2.82843

Example 3:

Input: positions = [[1,1]]
Output: 0.00000

Example 4:

Input: positions = [[1,1],[0,0],[2,0]]
Output: 2.73205
Explanation: At the first glance, you may think that locating the centre at [1, 0] will achieve the minimum sum, but locating it at [1, 0] will make the sum of distances = 3.
Try to locate the centre at [1.0, 0.5773502711] you will see that the sum of distances is 2.73205.
Be careful with the precision!

Example 5:

Input: positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]]
Output: 32.94036
Explanation: You can use [4.3460852395, 4.9813795505] as the position of the centre.

Constraints:

1 <= positions.length <= 50
positions[i].length == 2
0 <= positions[i][0], positions[i][1] <= 100

Solution: Weiszfeld’s algorithm

Use Weiszfeld’s algorithm to compute geometric median of the samples.

Time complexity: O(f(epsilon) * O)
Space complexity: O(1)

C++

template<typename T1, typename T2>

double dist(const vector<T1>& a, const vector<T2>& b) {

return sqrt((a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]));

};

class Solution {

public:

double getMinDistSum(vector<vector<int>>& positions) {

constexpr double kDelta = 1e-7;

constexpr double kEpsilon = 1e-15;

vector<double> c{-1, -1};

double ans = 0;

while (true) {

ans = 0;

double nx = 0, ny = 0;

double denominator = 0;

for (const auto& p : positions) {

double d = dist(c, p) + kEpsilon;

ans += d;

nx += p[0] / d;

ny += p[1] / d;

denominator += 1.0 / d;

}

vector<double> t{nx / denominator, ny / denominator};

if (dist(c, t) < kDelta) return ans;

c = t;

}

return -1;

}

};

花花酱 LeetCode 1637. Widest Vertical Area Between Two Points Containing No Points

By zxi on October 31, 2020

Given n points on a 2D plane where points[i] = [x_i, y_i], Return the widest vertical area between two points such that no points are inside the area.

A vertical area is an area of fixed-width extending infinitely along the y-axis (i.e., infinite height). The widest vertical area is the one with the maximum width.

Note that points on the edge of a vertical area are not considered included in the area.

Example 1:

Input: points = [[8,7],[9,9],[7,4],[9,7]]
Output: 1
Explanation: Both the red and the blue area are optimal.

Example 2:

Input: points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
Output: 3

Constraints:

n == points.length
2 <= n <= 10⁵
points[i].length == 2
0 <= x_i, y_i <= 10⁹

Solution: Sort by x coordinates

Time complexity: O(nlogn)
Space complexity: O(n)

C++

class Solution {

public:

int maxWidthOfVerticalArea(vector<vector<int>>& points) {

sort(begin(points), end(points), [](const auto& p1, const auto& p2) {

return p1[0] != p2[0] ? p1[0] < p2[0] : p1[1] < p2[1];

});

int ans = 0;

for (int i = 1; i < points.size(); ++i)

ans = max(ans, points[i][0] - points[i - 1][0]);

return ans;

}

};