Posts published in “Search”

花花酱 LeetCode 2002. Maximum Product of the Length of Two Palindromic Subsequences

By zxi on November 20, 2021

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return the maximum possible product of the lengths of the two palindromic subsequences.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

Example 1:

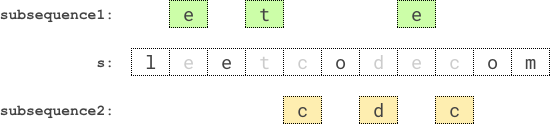
Input: s = "leetcodecom"
Output: 9
Explanation: An optimal solution is to choose "ete" for the 1^st subsequence and "cdc" for the 2^nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = "bb"
Output: 1
Explanation: An optimal solution is to choose "b" (the first character) for the 1^st subsequence and "b" (the second character) for the 2^nd subsequence.
The product of their lengths is: 1 * 1 = 1.

Example 3:

Input: s = "accbcaxxcxx"
Output: 25
Explanation: An optimal solution is to choose "accca" for the 1^st subsequence and "xxcxx" for the 2^nd subsequence.
The product of their lengths is: 5 * 5 = 25.

Constraints:

2 <= s.length <= 12
s consists of lowercase English letters only.

Solution 1: DFS

Time complexity: O(3ⁿ*n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maxProduct(string s) {

auto isPalindrom = [](const string& s) {

for (int i = 0; i < s.length(); ++i)

if (s[i] != s[s.size() - i - 1]) return false;

return true;

};

const int n = s.size();

vector<string> ss(3);

size_t ans = 0;

function<void(int)> dfs = [&](int i) -> void {

if (i == n) {

if (isPalindrom(ss[0]) && isPalindrom(ss[1]))

ans = max(ans, ss[0].size() * ss[1].size());

return;

}

for (int k = 0; k < 3; ++k) {

ss[k].push_back(s[i]);

dfs(i + 1);

ss[k].pop_back();

}

};

dfs(0);

return ans;

}

};

Solution: Subsets + Bitmask + All Pairs

Time complexity: O(2²ⁿ)
Space complexity: O(2ⁿ)

C++

// Author: Huahua

class Solution {

public:

int maxProduct(string s) {

auto isPalindrom = [](const string& s) {

for (int i = 0; i < s.length(); ++i)

if (s[i] != s[s.size() - i - 1]) return false;

return true;

};

const int n = s.size();

unordered_set<int> p;

for (int i = 0; i < (1 << n); ++i) {

string t;

for (int j = 0; j < n; ++j)

if (i >> j & 1) t.push_back(s[j]);

if (isPalindrom(t))

p.insert(i);

}

int ans = 0;

for (int s1 : p)

for (int s2 : p)

if (!(s1 & s2))

ans = max(ans, __builtin_popcount(s1) * __builtin_popcount(s2));

return ans;

}

};

花花酱 LeetCode 2065. Maximum Path Quality of a Graph

By zxi on November 7, 2021

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the i^th node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [u_j, v_j, time_j] indicates that there is an undirected edge between the nodes u_j and v_j,and it takes time_j seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node’s value is added at most once to the sum).

Return the maximum quality of a valid path.

Note: There are at most four edges connected to each node.

Example 1:

Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2:

Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3:

Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Example 4:

Input: values = [0,1,2], edges = [[1,2,10]], maxTime = 10
Output: 0
Explanation: 
The only path is 0. The total time taken is 0.
The only node visited is 0, giving a maximal path quality of 0.

Constraints:

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
All the pairs [u_j, v_j] are unique.
There are at most four edges connected to each node.
The graph may not be connected.

Solution: DFS

Given time >= 10 and maxTime <= 100, the path length is at most 10, given at most four edges connected to each node.
Time complexity: O(4¹⁰)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maximalPathQuality(vector<int>& values, vector<vector<int>>& edges, int maxTime) {

const int n = values.size();

vector<vector<pair<int, int>>> g(n);

for (const auto& e : edges) {

g[e[0]].emplace_back(e[1], e[2]);

g[e[1]].emplace_back(e[0], e[2]);

}

vector<int> seen(n);

int ans = 0;

function<void(int, int, int)> dfs = [&](int u, int t, int s) {

if (++seen[u] == 1) s += values[u];

if (u == 0) ans = max(ans, s);

for (auto [v, d] : g[u])

if (t + d <= maxTime) dfs(v, t + d, s);

if (--seen[u] == 0) s -= values[u];

};

dfs(0, 0, 0);

return ans;

}

};

花花酱 LeetCode 2059. Minimum Operations to Convert Number

By zxi on November 4, 2021

You are given a 0-indexed integer array nums containing distinct numbers, an integer start, and an integer goal. There is an integer x that is initially set to start, and you want to perform operations on x such that it is converted to goal. You can perform the following operation repeatedly on the number x:

If 0 <= x <= 1000, then for any index i in the array (0 <= i < nums.length), you can set x to any of the following:

x + nums[i]
x - nums[i]
x ^ nums[i] (bitwise-XOR)

Note that you can use each nums[i] any number of times in any order. Operations that set x to be out of the range 0 <= x <= 1000 are valid, but no more operations can be done afterward.

Return the minimum number of operations needed to convert x = start into goal, and -1 if it is not possible.

Example 1:

Input: nums = [1,3], start = 6, goal = 4
Output: 2
Explanation:
We can go from 6 → 7 → 4 with the following 2 operations.
- 6 ^ 1 = 7
- 7 ^ 3 = 4

Example 2:

Input: nums = [2,4,12], start = 2, goal = 12
Output: 2
Explanation:
We can go from 2 → 14 → 12 with the following 2 operations.
- 2 + 12 = 14
- 14 - 2 = 12

Example 3:

Input: nums = [3,5,7], start = 0, goal = -4
Output: 2
Explanation:
We can go from 0 → 3 → -4 with the following 2 operations. 
- 0 + 3 = 3
- 3 - 7 = -4
Note that the last operation sets x out of the range 0 <= x <= 1000, which is valid.

Example 4:

Input: nums = [2,8,16], start = 0, goal = 1
Output: -1
Explanation:
There is no way to convert 0 into 1.

Example 5:

Input: nums = [1], start = 0, goal = 3

Output: 3

Explanation:

We can go from 0 → 1 → 2 → 3 with the following 3 operations.

- 0 + 1 = 1

- 1 + 1 = 2

- 2 + 1 = 3

Constraints:

1 <= nums.length <= 1000
-10⁹ <= nums[i], goal <= 10⁹
0 <= start <= 1000
start != goal
All the integers in nums are distinct.

Solution: BFS

Time complexity: O(n*m)
Space complexity: O(m)

C++

// Author: Huahua

class Solution {

public:

int minimumOperations(vector<int>& nums, int start, int goal) {

vector<int> seen(1001);

queue<int> q{{start}};

for (int ans = 1, s = 1; !q.empty(); ++ans, s = q.size()) {

while (s--) {

int x = q.front(); q.pop();

for (int n : nums)

for (int t : {x + n, x - n, x ^ n})

if (t == goal)

return ans;

else if (t < 0 || t > 1000 || seen[t]++)

continue;

else

q.push(t);

}

return -1;

}

};

花花酱 LeetCode 2048. Next Greater Numerically Balanced Number

By zxi on October 25, 2021

An integer x is numerically balanced if for every digit d in the number x, there are exactly d occurrences of that digit in x.

Given an integer n, return the smallest numerically balanced number strictly greater than n.

Example 1:

Input: n = 1
Output: 22
Explanation: 
22 is numerically balanced since:
- The digit 2 occurs 2 times. 
It is also the smallest numerically balanced number strictly greater than 1.

Example 2:

Input: n = 1000
Output: 1333
Explanation: 
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times. 
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.

Example 3:

Input: n = 3000
Output: 3133
Explanation: 
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.

Constraints:

0 <= n <= 10⁶

Solution: Permutation

Time complexity: O(log(n)!)
Space complexity: O(log(n)) ?

C++

// Author: Huahua

class Solution {

public:

int nextBeautifulNumber(int n) {

const string t = to_string(n);

vector<int> nums{1,

22,

122, 333,

1333, 4444,

14444, 22333, 55555,

122333, 155555, 224444, 666666};

int ans = 1224444;

for (int num : nums) {

string s = to_string(num);

if (s.size() < t.size()) continue;

else if (s.size() > t.size()) {

ans = min(ans, num);

} else { // same length

do {

if (s > t) ans = min(ans, stoi(s));

} while (next_permutation(begin(s), end(s)));

}

return ans;

}

};

花花酱 LeetCode 2044. Count Number of Maximum Bitwise-OR Subsets

By zxi on October 17, 2021

Given an integer array nums, find the maximum possible bitwise OR of a subset of nums and return the number of different non-empty subsets with the maximum bitwise OR.

An array a is a subset of an array b if a can be obtained from b by deleting some (possibly zero) elements of b. Two subsets are considered different if the indices of the elements chosen are different.

The bitwise OR of an array a is equal to a[0] OR a[1] OR ... OR a[a.length - 1] (0-indexed).

Example 1:

Input: nums = [3,1]
Output: 2
Explanation: The maximum possible bitwise OR of a subset is 3. There are 2 subsets with a bitwise OR of 3:
- [3]
- [3,1]

Example 2:

Input: nums = [2,2,2]
Output: 7
Explanation: All non-empty subsets of [2,2,2] have a bitwise OR of 2. There are 2³ - 1 = 7 total subsets.

Example 3:

Input: nums = [3,2,1,5]
Output: 6
Explanation: The maximum possible bitwise OR of a subset is 7. There are 6 subsets with a bitwise OR of 7:
- [3,5]
- [3,1,5]
- [3,2,5]
- [3,2,1,5]
- [2,5]
- [2,1,5]

Constraints:

1 <= nums.length <= 16
1 <= nums[i] <= 10⁵

Solution: Brute Force

Try all possible subsets

Time complexity: O(n*2ⁿ)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int countMaxOrSubsets(vector<int>& nums) {

const int n = nums.size();

int max_or = 0;

int count = 0;

for (int s = 0; s < 1 << n; ++s) {

int cur_or = 0;

for (int i = 0; i < n; ++i)

if (s >> i & 1) cur_or |= nums[i];

if (cur_or > max_or) {

max_or = cur_or;

count = 1;

} else if (cur_or == max_or) {

++count;

}

return count;

}

};