Posts published in “Tree”

花花酱 LeetCode 295. Find Median from Data Stream O(logn) + O(1)

By zxi on September 12, 2017

Problem:

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

Examples:

[2,3,4] , the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

void addNum(int num) – Add a integer number from the data stream to the data structure.
double findMedian() – Return the median of all elements so far.

For example:

addNum(1)

addNum(2)

findMedian() = 1.5

addNum(3)

findMedian() = 2

Idea:

Min/Max heap
Balanced binary search tree

Time Complexity:

add(num): O(logn)

findMedian(): O(logn)

Solution1:

// Author: Huahua

// Running Time: 152 ms

class MedianFinder {

public:

/** initialize your data structure here. */

MedianFinder() {}

// l_.size() >= r_.size()

void addNum(int num) {

if (l_.empty() || num <= l_.top()) {

l_.push(num);

} else {

r_.push(num);

}

// Step 2: Balence left/right

if (l_.size() < r_.size()) {

l_.push(r_.top());

r_.pop();

} else if (l_.size() - r_.size() == 2) {

r_.push(l_.top());

l_.pop();

}

double findMedian() {

if (l_.size() > r_.size()) {

return static_cast<double>(l_.top());

} else {

return (static_cast<double>(l_.top()) + r_.top()) / 2;

}

private:

priority_queue<int, vector<int>, less<int>> l_; // max-heap

priority_queue<int, vector<int>, greater<int>> r_; // min-heap

};

Solution 2:

// Author: Huahua

// Running time: 172 ms

class MedianFinder {

public:

/** initialize your data structure here. */

MedianFinder(): l_(m_.cend()), r_(m_.cend()) {}

// O(logn)

void addNum(int num) {

if (m_.empty()) {

l_ = r_ = m_.insert(num);

return;

}

m_.insert(num);

const size_t n = m_.size();

if (n & 1) {

// odd number

if (num >= *r_) {

l_ = r_;

} else {

// num < *r_, l_ could be invalidated

l_ = --r_;

}

} else {

if (num >= *r_)

++r_;

else

--l_;

}

// O(1)

double findMedian() {

return (static_cast<double>(*l_) + *r_) / 2;

}

private:

multiset<int> m_;

multiset<int>::const_iterator l_; // current left median

multiset<int>::const_iterator r_; // current right median

};

Related Problems

花花酱 LeetCode 145. Binary Tree Postorder Traversal

By zxi on September 8, 2017

Problem:

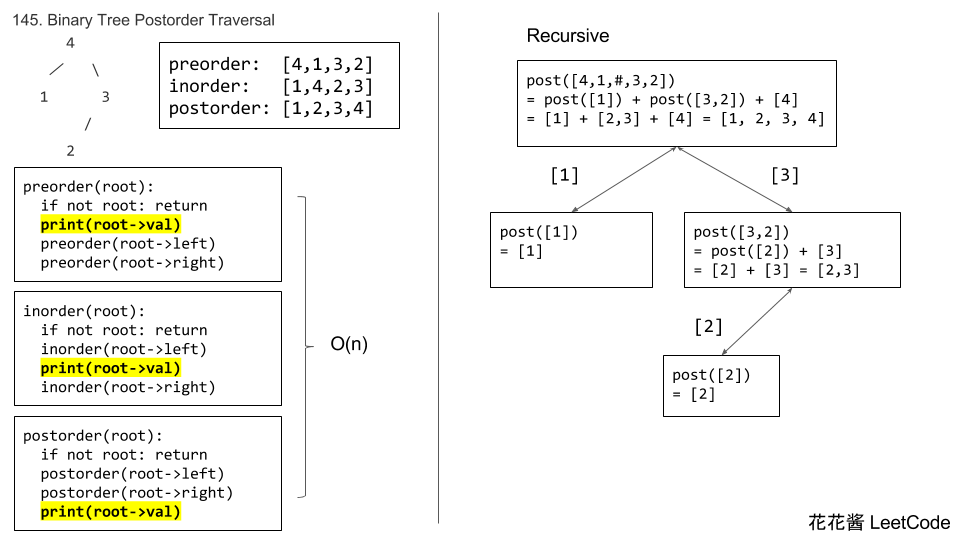
Given a binary tree, return the postorder traversal of its nodes’ values.

For example:
Given binary tree {1,#,2,3},

return [3,2,1].

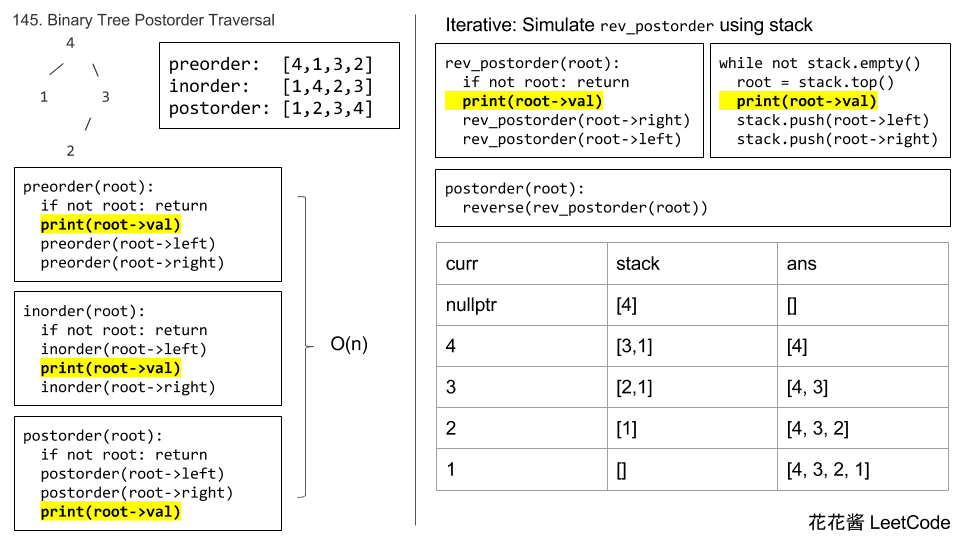
Note: Recursive solution is trivial, could you do it iteratively?

Solution 1:

// Author: Huahua

class Solution {

public:

vector<int> postorderTraversal(TreeNode* root) {

vector<int> ans;

postorderTraversal(root, ans);

return ans;

}

void postorderTraversal(TreeNode* root, vector<int>& ans) {

if (!root) return;

postorderTraversal(root->left, ans);

postorderTraversal(root->right, ans);

ans.push_back(root->val);

}

};

Solution 2:

// Author: Huahua

class Solution {

public:

vector<int> postorderTraversal(TreeNode* root) {

if (!root) return {};

vector<int> ans;

const vector<int> l = postorderTraversal(root->left);

const vector<int> r = postorderTraversal(root->right);

ans.insert(ans.end(), l.begin(), l.end());

ans.insert(ans.end(), r.begin(), r.end());

ans.push_back(root->val);

return ans;

}

};

Solution 3:

// Author: Huahua

class Solution {

public:

vector<int> postorderTraversal(TreeNode* root) {

if (!root) return {};

deque<int> ans;

stack<TreeNode*> s;

s.push(root);

while (!s.empty()) {

TreeNode* n = s.top();

s.pop();

ans.push_front(n->val); // O(1)

if (n->left) s.push(n->left);

if (n->right) s.push(n->right);

}

return vector<int>(ans.begin(), ans.end());

}

};

花花酱 LeetCode 637. Average of Levels in Binary Tree

By zxi on September 7, 2017

Problem:

Given a non-empty binary tree, return the average value of the nodes on each level in the form of an array.

Example 1:

Input:

/ \

9 20

/ \

15 7

Output: [3, 14.5, 11]

Explanation:

The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.

Hence return [3, 14.5, 11].

Time Complexity:

O(n)

Space Complexity:

O(h)

Solution 1:

BFS

// Author: Huahua

class Solution {

public:

vector<double> averageOfLevels(TreeNode* root) {

if(root == nullptr) return {};

vector<double> ans;

vector<TreeNode*> curr, next;

curr.push_back(root);

// process every level one by one

while(!curr.empty()) {

long long sum = 0;

for(const auto& node : curr) {

sum += node->val;

if (node->left) next.push_back(node->left);

if (node->right) next.push_back(node->right);

}

ans.push_back(static_cast<double>(sum) / curr.size());

curr.swap(next);

next.clear();

}

return ans;

}

};

Solution 2:

DFS

// Author: Huahua

class Solution {

public:

vector<double> averageOfLevels(TreeNode* root) {

if(root == nullptr) return {};

vector<pair<long long, int>> sum_count;

vector<double> ans;

preorder(root, 0, sum_count);

for(const auto& p : sum_count)

ans.push_back(static_cast<double>(p.first) / p.second);

return ans;

}

private:

void preorder(TreeNode* root, int depth, vector<pair<long long, int>>& sum_count) {

if(root == nullptr) return;

if(depth>=sum_count.size()) sum_count.push_back({0,0});

sum_count[depth].first += root->val;

++sum_count[depth].second;

preorder(root->left, depth+1, sum_count);

preorder(root->right, depth+1, sum_count);

}

};

Related Problems:

[解题报告] LeetCode 102. Binary Tree Level Order Traversal

花花酱 LeetCode 654. Maximum Binary Tree

By zxi on September 4, 2017

Given an integer array with no duplicates. A maximum tree building on this array is defined as follow:

The root is the maximum number in the array.
The left subtree is the maximum tree constructed from left part subarray divided by the maximum number.
The right subtree is the maximum tree constructed from right part subarray divided by the maximum number.

Construct the maximum tree by the given array and output the root node of this tree.

Example 1:

Input: [3,2,1,6,0,5]

Output: return the tree root node representing the following tree:

/ \

3 5

\ /

2 0

Idea:

Recursion

Solution:

With copy

Time complexity: O(nlogn) ~ O(n^2)

Space complexity: O(nlogn) ~ O(n^2)

running time 79ms

// Author: Huahua

class Solution {

public:

TreeNode* constructMaximumBinaryTree(vector<int>& nums) {

if(nums.empty()) return nullptr;

auto it = std::max_element(nums.begin(), nums.end());

TreeNode* root=new TreeNode(*it);

vector<int> left(nums.begin(), it);

vector<int> right(it+1, nums.end());

root->left = constructMaximumBinaryTree(left);

root->right = constructMaximumBinaryTree(right);

return root;

}

Without copy

Time complexity: O(nlogn) ~ O(n^2)

Space complexity: O(logn) ~ O(n)

running time 66ms

// Author: Huahua

class Solution {

public:

TreeNode* constructMaximumBinaryTree(vector<int>& nums) {

return makeMBT(nums, 0, nums.size());

}

private:

TreeNode* makeMBT(const vector<int>& nums, int begin, int end) {

if(begin>=end) return nullptr;

auto it = std::max_element(nums.begin() + begin, nums.begin() + end);

TreeNode* root=new TreeNode(*it);

int index = it - nums.begin();

root->left = makeMBT(nums, begin, index);

root->right = makeMBT(nums, index+1, end);

return root;

}

};

花花酱 LeetCode 669. Trim a Binary Search Tree

By zxi on September 4, 2017

Given a binary search tree and the lowest and highest boundaries as L and R, trim the tree so that all its elements lies in [L, R] (R >= L). You might need to change the root of the tree, so the result should return the new root of the trimmed binary search tree.

Example 1:

Input:

/ \

0 2

L = 1

R = 2

Output:

Example 2:

Input:

/ \

0 4

L = 1

R = 3

Output:

This problem can be solved with recursion

There 3 cases in total depends on the root value and L, R

Time complexity: O(n)

Space complexity: O(1)

Solution:

// Author: Huahua

class Solution {

public:

// No cleanup -> memory leak

TreeNode* trimBST(TreeNode* root, int L, int R) {

if(!root) return nullptr;

// val not in range, return the left/right subtrees

if(root->val < L) return trimBST(root->right, L, R);

if(root->val > R) return trimBST(root->left, L, R);

// val in [L, R], recusively trim left/right subtrees

root->left = trimBST(root->left, L, R);

root->right = trimBST(root->right, L, R);

return root;

}

};

The previous solution has potential memory leak for languages without garbage collection.

Here’s the full program to delete trimmed nodes.

// Author: Huahua

#include <iostream>

using namespace std;

struct TreeNode {

int val;

TreeNode *left;

TreeNode *right;

TreeNode(int x) : val(x), left(NULL), right(NULL) {}

};

class Solution {

public:

// With cleanup -> no memory leak

TreeNode*& trimBST(TreeNode*& root, int L, int R) {

if(!root) return root;

if(root->val < L) {

auto& result = trimBST(root->right, L, R);

deleteTree(root->left);

delete root;

root=nullptr;

return result;

} else if(root->val > R) {

auto& result = trimBST(root->left, L, R);

deleteTree(root->right);

delete root;

root=nullptr;

return result;

} else {

// recusively trim left/right subtrees

root->left = trimBST(root->left, L, R);

root->right = trimBST(root->right, L, R);

return root;

}

void deleteTree(TreeNode* &root) {

if(!root) return;

deleteTree(root->left);

deleteTree(root->right);

delete root;

root=nullptr;

}

};

void PrintTree(TreeNode* root) {

if(!root) {

cout<<"null ";

return;

};

if(!root->left && !root->right) {

cout<<root->val<<" ";

} else {

cout<<root->val<<" ";

PrintTree(root->left);

PrintTree(root->right);

}

int main()

{

TreeNode* root=new TreeNode(2);

root->left=new TreeNode(1);

root->right=new TreeNode(3);

PrintTree(root);

std::cout<<std::endl;

TreeNode* t = Solution().trimBST(root, 3, 4);

PrintTree(t);

std::cout<<std::endl;

// Original root was deleted

PrintTree(root);

std::cout<<std::endl;

return 0;

}

Example output

2 1 3

null