花花酱 LeetCode 1799. Maximize Score After N Operations

You are given nums, an array of positive integers of size 2 * n. You must perform n operations on this array.

In the ith operation (1-indexed), you will:

• Choose two elements, x and y.
• Receive a score of i * gcd(x, y).
• Remove x and y from nums.

Return the maximum score you can receive after performing n operations.

The function gcd(x, y) is the greatest common divisor of x and y.

Example 1:

Input: nums = [1,2]
Output: 1
Explanation: The optimal choice of operations is:
(1 * gcd(1, 2)) = 1

Example 2:

Input: nums = [3,4,6,8]
Output: 11
Explanation: The optimal choice of operations is:
(1 * gcd(3, 6)) + (2 * gcd(4, 8)) = 3 + 8 = 11

Example 3:

Input: nums = [1,2,3,4,5,6]
Output: 14
Explanation: The optimal choice of operations is:
(1 * gcd(1, 5)) + (2 * gcd(2, 4)) + (3 * gcd(3, 6)) = 1 + 4 + 9 = 14

Constraints:

• 1 <= n <= 7
• nums.length == 2 * n
• 1 <= nums[i] <= 106

Solution: Mask DP

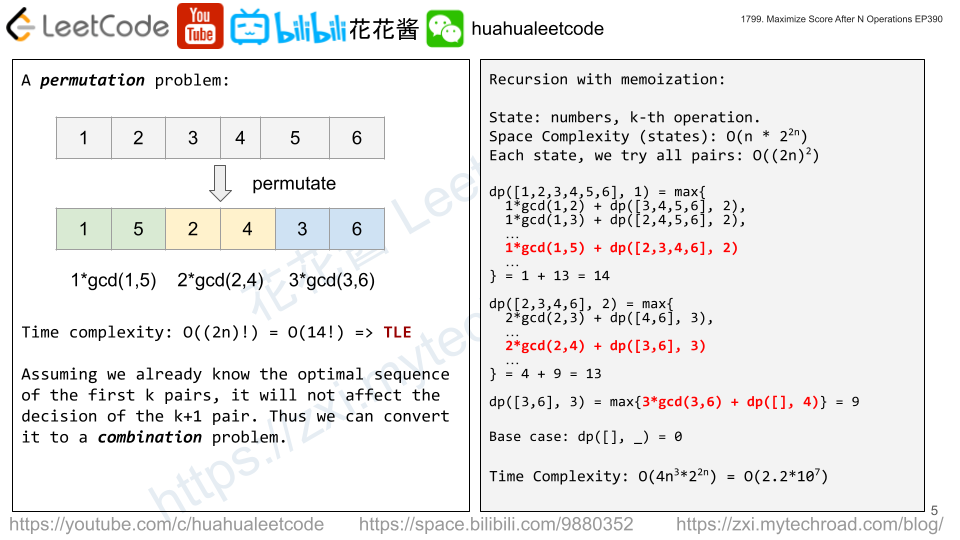
dp(mask, i) := max score of numbers (represented by a binary mask) at the i-th operations.
ans = dp(1, mask)
base case: dp = 0 if mask == 0
Transition: dp(mask, i) = max(dp(new_mask, i + 1) + i * gcd(nums[m], nums[n]))

Time complexity: O(n²*2²ⁿ)
Space complexity: O(2²ⁿ)

Bottom-Up