Problem

Given several boxes with different colors represented by different positive numbers.
You may experience several rounds to remove boxes until there is no box left. Each time you can choose some continuous boxes with the same color (composed of k boxes, k >= 1), remove them and get k*k points.
Find the maximum points you can get.

Example 1:
Input:

1	[1, 3, 2, 2, 2, 3, 4, 3, 1]

Output:

Explanation:

[1, 3, 2, 2, 2, 3, 4, 3, 1] 
----> [1, 3, 3, 4, 3, 1] (3*3=9 points) 
----> [1, 3, 3, 3, 1] (1*1=1 points) 
----> [1, 1] (3*3=9 points) 
----> [] (2*2=4 points)

Note: The number of boxes n would not exceed 100.

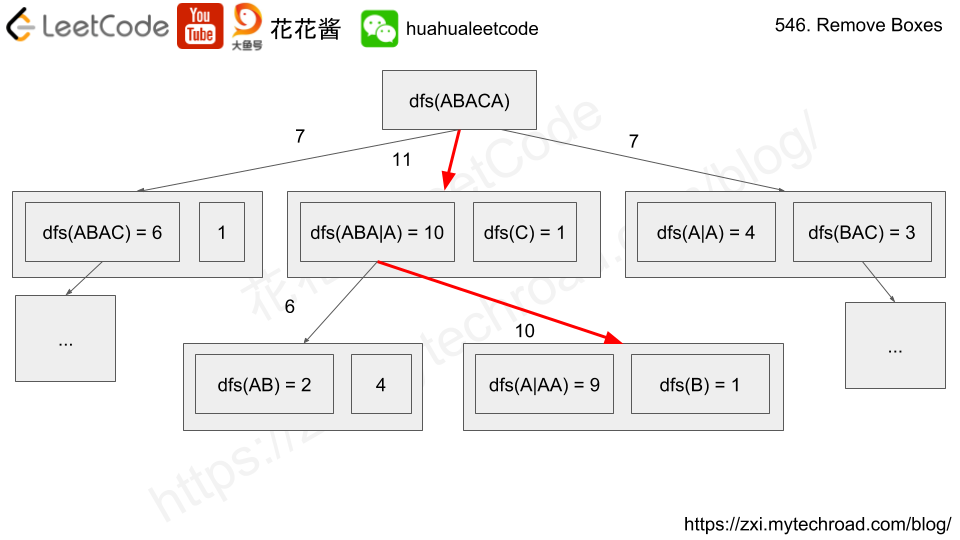
Solution: Recursion + Memorization

Use dp[l][r][k] to denote the max score of subarray box[l] ~ box[r] with k boxes after box[r] that have the same color as box[r]

box[l], box[l+1], …, box[r], box[r+1], …, box[r+k]

e.g. “CDABACAAAAA”

dp[2][6][4] is the max score of [ABACA] followed by [AAAA]
dp[2][6][3] is the max score of [ABACA] followed by [AAA]

base case: l > r, empty array, return 0.

Transition:
dp[l][r][k] = max(dp[l][r-1][0] + (k + 1)*(k + 1),  # case 1
                  dp[l][i][k+1] + dp[i+1][r-1][0])  # case 2
# "ABACA|AAAA" 
# case 1: dp("ABAC") + score("AAAAA") drop j and the tail.
# case 2: box[i] == box[r], l <= i < r, try all break points
# max({dp("A|AAAAA") + dp("BAC")}, {dp("ABA|AAAAA") + dp("C")})

Time complexity: O(n^4)

Space complexity: O(n^3)

C++

// Author: Huahua

// Running time: 196 ms

class Solution {

public:

int removeBoxes(vector<int>& boxes) {

const int n = boxes.size();

m_ = vector<vector<vector<int>>>(n, vector<vector<int>>(n, vector<int>(n)));

return dfs(boxes, 0, n - 1, 0);

}

private:

vector<vector<vector<int>>> m_;

int dfs(const vector<int>& boxes, int l, int r, int k) {

if (l > r) return 0;

if (m_[l][r][k] > 0) return m_[l][r][k];

m_[l][r][k] = dfs(boxes, l, r - 1, 0) + (k + 1) * (k + 1);

for (int i = l; i < r; ++i)

if (boxes[i] == boxes[r])

m_[l][r][k] = max(m_[l][r][k], dfs(boxes, l, i, k + 1) + dfs(boxes, i + 1, r - 1, 0));

return m_[l][r][k];

}

};

Optimized

// Author: Huahua

// Running time: 16 ms

int m[100][100][100];

class Solution {

public:

int removeBoxes(vector<int>& boxes) {

memset(m, 0, sizeof(m));

return dfs(boxes, 0, boxes.size() - 1, 0);

}

private:

int dfs(const vector<int>& boxes, int l, int r, int k) {

if (l > r) return 0;

if (m[l][r][k] > 0) return m[l][r][k];

int rr = r;

int kk = k;

while (l < r && boxes[r - 1] == boxes[r]) {--r; ++k;}

m[l][r][k] = dfs(boxes, l, r - 1, 0) + (k + 1) * (k + 1);

for (int i = l; i < r; ++i)

if (boxes[i] == boxes[r])

m[l][r][k] = max(m[l][r][k], dfs(boxes, l, i, k + 1) + dfs(boxes, i + 1, r - 1, 0));

for (int d = 1; d <= r - rr; ++d)

m[l][r + d][k - d] = m[l][r][k];

return m[l][r][k];

}

};

Use a HashTable to replace the 3D DP array since the DP array could be sparse when many consecutive boxes are the same color.

// Author: Huahua

// Running time: 8 ms (beats 100%)

class Solution {

public:

int removeBoxes(vector<int>& boxes) {

len_ = vector<int>(boxes.size());

for (int i = 1; i < boxes.size(); ++i)

if (boxes[i] == boxes[i - 1]) len_[i] = len_[i - 1] + 1;

return dfs(boxes, 0, boxes.size() - 1, 0);

}

private:

unordered_map<int, int> m_;

vector<int> len_;

int dfs(const vector<int>& boxes, int l, int r, int k) {

if (l > r) return 0;

k += len_[r];

r -= len_[r];

int key = (l * 100 + r) * 100 + k;

auto it = m_.find(key);

if (it != m_.end()) return it->second;

int& ans = m_[key];

ans = dfs(boxes, l, r - 1, 0) + (k + 1) * (k + 1);

for (int i = l; i < r; ++i)

if (boxes[i] == boxes[r])

ans = max(ans, dfs(boxes, l, i, k + 1) + dfs(boxes, i + 1, r - 1, 0));

return ans;

}

};

花花酱 LeetCode 546. Remove Boxes

Problem

Solution: Recursion + Memorization

Related Problems

Be First to Comment

Leave a Reply Cancel reply