Huahua's Tech Road

花花酱 LeetCode 1478. Allocate Mailboxes

By zxi on June 14, 2020

Given the array houses and an integer k. where houses[i] is the location of the ith house along a street, your task is to allocate k mailboxes in the street.

Return the minimum total distance between each house and its nearest mailbox.

The answer is guaranteed to fit in a 32-bit signed integer.

Example 1:

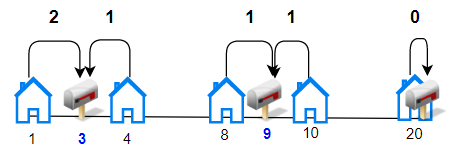
Input: houses = [1,4,8,10,20], k = 3
Output: 5
Explanation: Allocate mailboxes in position 3, 9 and 20.
Minimum total distance from each houses to nearest mailboxes is |3-1| + |4-3| + |9-8| + |10-9| + |20-20| = 5

Example 2:

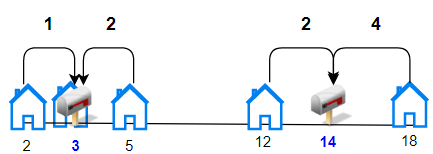
Input: houses = [2,3,5,12,18], k = 2
Output: 9
Explanation: Allocate mailboxes in position 3 and 14.
Minimum total distance from each houses to nearest mailboxes is |2-3| + |3-3| + |5-3| + |12-14| + |18-14| = 9.

Example 3:

Input: houses = [7,4,6,1], k = 1
Output: 8

Example 4:

Input: houses = [3,6,14,10], k = 4
Output: 0

Constraints:

n == houses.length
1 <= n <= 100
1 <= houses[i] <= 10^4
1 <= k <= n
Array houses contain unique integers.

Solution: DP

First, we need to sort the houses by their location.

This is a partitioning problem, e.g. optimal solution to partition first N houses into K groups. (allocating K mailboxes for the first N houses).

The key of this problem is to solve a base case, optimally allocating one mailbox for houses[i~j], The intuition is to put the mailbox in the middle location, this only works if there are only tow houses, or all the houses are evenly distributed. The correct location is the “median position” of a set of houses. For example, if the sorted locations are [1,2,3,100], the average will be 26 which costs 146 while the median is 2, and the cost becomes 100.

dp[i][k] := min cost to allocate k mailboxes houses[0~i].

base cases:

dp[i][1] = cost(0, i), min cost to allocate one mailbox.
dp[i][k] = 0 if k > i, more mailboxes than houses. // this is actually a pruning.

transition:

dp[i][k] = min(dp[p][k-1] + cost(p + 1, i)) 0 <= p < i,

allocate k-1 mailboxes for houses[0~p], and allocate one for houses[p+1~i]

ans:

dp[n-1][k]

Time complexity: O(n^3)
Space complexity: O(n^2) -> O(n)

C++

// Author: Huahua

class Solution {

public:

int minDistance(vector<int>& houses, int k) {

constexpr int kInf = 1e9;

const int n = houses.size();

sort(begin(houses), end(houses));

vector<vector<int>> dp(n + 1, vector<int>(n + 1, kInf));

vector<vector<int>> costs(n + 1, vector<int>(n + 1, kInf));

// min cost to allocate one mailbox for houses[i~j].

auto cost = [&](int i, int j) {

int& ans = costs[i][j];

if (ans != kInf) return ans;

const int m = i + (j - i) / 2;

int box = 0;

if ((j - i + 1) & 1) // odd number of houses.

box = houses[m];

else // even number of houses.

box = (houses[m] + houses[m + 1]) / 2;

ans = 0;

for (int h = i; h <= j; ++h)

ans += abs(houses[h] - box);

return ans;

};

// min cost to allocate k mailboxes for houses[0~i].

function<int(int, int)> solve = [&](int i, int k) {

if (k > i) return 0; // more mailboxs than houses.

if (k == 1) return cost(0, i);

int& ans = dp[i][k];

if (ans != kInf) return ans;

for (int p = 0; p < i; ++p)

ans = min(ans, solve(p, k - 1) + cost(p + 1, i));

return ans;

};

return solve(n - 1, k);

}

};

O(1) time to compute cost. O(n) Time and space for pre-processing.

C++

// Author: Huahua

vector<int> sums(n + 1);

for (int i = 1; i <= n; ++i)

sums[i] = sums[i - 1] + houses[i - 1];

// min cost to allocate one mailbox for houses[i~j].

auto cost = [&](int i, int j) {

const int m1 = (i + j) / 2;

const int m2 = (i + j + 1) / 2;

const int center = (houses[m1] + houses[m2]) / 2;

return (m1 - i + 1) * center - (sums[m1 + 1] - sums[i])

+ (sums[j + 1] - sums[m2]) - (j - m2 + 1) * center;

};

花花酱 LeetCode 1477. Find Two Non-overlapping Sub-arrays Each With Target Sum

By zxi on June 13, 2020

Given an array of integers arr and an integer target.

You have to find two non-overlapping sub-arrays of arr each with sum equal target. There can be multiple answers so you have to find an answer where the sum of the lengths of the two sub-arrays is minimum.

Return the minimum sum of the lengths of the two required sub-arrays, or return -1 if you cannot find such two sub-arrays.

Example 1:

Input: arr = [3,2,2,4,3], target = 3
Output: 2
Explanation: Only two sub-arrays have sum = 3 ([3] and [3]). The sum of their lengths is 2.

Example 2:

Input: arr = [7,3,4,7], target = 7
Output: 2
Explanation: Although we have three non-overlapping sub-arrays of sum = 7 ([7], [3,4] and [7]), but we will choose the first and third sub-arrays as the sum of their lengths is 2.

Example 3:

Input: arr = [4,3,2,6,2,3,4], target = 6
Output: -1
Explanation: We have only one sub-array of sum = 6.

Example 4:

Input: arr = [5,5,4,4,5], target = 3
Output: -1
Explanation: We cannot find a sub-array of sum = 3.

Example 5:

Input: arr = [3,1,1,1,5,1,2,1], target = 3
Output: 3
Explanation: Note that sub-arrays [1,2] and [2,1] cannot be an answer because they overlap.

Constraints:

1 <= arr.length <= 10^5
1 <= arr[i] <= 1000
1 <= target <= 10^8

Solution: Sliding Window + Best so far

Use a sliding window to maintain a subarray whose sum is <= target
When the sum of the sliding window equals to target, we found a subarray [s, e]
Update ans with it’s length + shortest subarray which ends before s.
We can use an array to store the shortest subarray which ends before s.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int minSumOfLengths(vector<int>& arr, int target) {

constexpr int kInf = 1e9;

const int n = arr.size();

// min_lens[i] := min length of a valid subarray ends or before i.

vector<int> min_lens(n, kInf);

int ans = kInf;

int sum = 0;

int s = 0;

int min_len = kInf;

for (int e = 0; e < n; ++e) {

sum += arr[e];

while (sum > target) sum -= arr[s++];

if (sum == target) {

const int cur_len = e - s + 1;

if (s > 0 && min_lens[s - 1] != kInf)

ans = min(ans, cur_len + min_lens[s - 1]);

min_len = min(min_len, cur_len);

}

min_lens[e] = min_len;

}

return ans >= kInf ? -1 : ans;

}

};

花花酱 LeetCode 1476. Subrectangle Queries

By zxi on June 13, 2020

Implement the class SubrectangleQueries which receives a rows x cols rectangle as a matrix of integers in the constructor and supports two methods:

1. updateSubrectangle(int row1, int col1, int row2, int col2, int newValue)

Updates all values with newValue in the subrectangle whose upper left coordinate is (row1,col1) and bottom right coordinate is (row2,col2).

2. getValue(int row, int col)

Returns the current value of the coordinate (row,col) from the rectangle.

Example 1:

Input
["SubrectangleQueries","getValue","updateSubrectangle","getValue","getValue","updateSubrectangle","getValue","getValue"]
[[[[1,2,1],[4,3,4],[3,2,1],[1,1,1]]],[0,2],[0,0,3,2,5],[0,2],[3,1],[3,0,3,2,10],[3,1],[0,2]]
Output

[null,1,null,5,5,null,10,5]

Explanation SubrectangleQueries subrectangleQueries = new SubrectangleQueries([[1,2,1],[4,3,4],[3,2,1],[1,1,1]]); // The initial rectangle (4×3) looks like: // 1 2 1 // 4 3 4 // 3 2 1 // 1 1 1 subrectangleQueries.getValue(0, 2); // return 1 subrectangleQueries.updateSubrectangle(0, 0, 3, 2, 5); // After this update the rectangle looks like: // 5 5 5 // 5 5 5 // 5 5 5 // 5 5 5 subrectangleQueries.getValue(0, 2); // return 5 subrectangleQueries.getValue(3, 1); // return 5 subrectangleQueries.updateSubrectangle(3, 0, 3, 2, 10); // After this update the rectangle looks like: // 5 5 5 // 5 5 5 // 5 5 5 // 10 10 10 subrectangleQueries.getValue(3, 1); // return 10 subrectangleQueries.getValue(0, 2); // return 5

Example 2:

Input
["SubrectangleQueries","getValue","updateSubrectangle","getValue","getValue","updateSubrectangle","getValue"]
[[[[1,1,1],[2,2,2],[3,3,3]]],[0,0],[0,0,2,2,100],[0,0],[2,2],[1,1,2,2,20],[2,2]]
Output

[null,1,null,100,100,null,20]

Explanation SubrectangleQueries subrectangleQueries = new SubrectangleQueries([[1,1,1],[2,2,2],[3,3,3]]); subrectangleQueries.getValue(0, 0); // return 1 subrectangleQueries.updateSubrectangle(0, 0, 2, 2, 100); subrectangleQueries.getValue(0, 0); // return 100 subrectangleQueries.getValue(2, 2); // return 100 subrectangleQueries.updateSubrectangle(1, 1, 2, 2, 20); subrectangleQueries.getValue(2, 2); // return 20

Constraints:

There will be at most 500 operations considering both methods: updateSubrectangle and getValue.
1 <= rows, cols <= 100
rows == rectangle.length
cols == rectangle[i].length
0 <= row1 <= row2 < rows
0 <= col1 <= col2 < cols
1 <= newValue, rectangle[i][j] <= 10^9
0 <= row < rows
0 <= col < cols

Solution 1: Simulation

Update the matrix values.

Time complexity:
Update: O(m*n), where m*n is the area of the sub-rectangle.
Query: O(1)

Space complexity: O(rows*cols)

C++

// Author: Huahua

class SubrectangleQueries {

public:

SubrectangleQueries(vector<vector<int>>& rectangle):

m_(rectangle) {}

void updateSubrectangle(int row1, int col1, int row2, int col2, int newValue) {

for (int i = row1; i <= row2; ++i)

for (int j = col1; j <= col2; ++j)

m_[i][j] = newValue;

}

int getValue(int row, int col) {

return m_[row][col];

}

private:

vector<vector<int>> m_;

};

Solution 2: Geometry

For each update remember the region and value.

For each query, find the newest updates that covers the query point. If not found, return the original value in the matrix.

Time complexity:
Update: O(1)
Query: O(|U|), where |U| is the number of updates so far.

Space complexity: O(|U|)

C++

// Author: Huahua

class SubrectangleQueries {

public:

SubrectangleQueries(vector<vector<int>>& rectangle):

m_(rectangle) {}

void updateSubrectangle(int row1, int col1, int row2, int col2, int newValue) {

updates_.push_front({row1, col1, row2, col2, newValue});

}

int getValue(int row, int col) {

for (const auto& u : updates_)

if (row >= u[0] && row <= u[2] && col >= u[1] && col <= u[3])

return u[4];

return m_[row][col];

}

private:

const vector<vector<int>>& m_;

deque<vector<int>> updates_;

};

花花酱 LeetCode 1475. Final Prices With a Special Discount in a Shop

By zxi on June 13, 2020

Given the array prices where prices[i] is the price of the ith item in a shop. There is a special discount for items in the shop, if you buy the ith item, then you will receive a discount equivalent to prices[j] where j is the minimum index such that j > i and prices[j] <= prices[i], otherwise, you will not receive any discount at all.

Return an array where the ith element is the final price you will pay for the ith item of the shop considering the special discount.

Example 1:

Input: prices = [8,4,6,2,3]
Output: [4,2,4,2,3]
Explanation: 
For item 0 with price[0]=8 you will receive a discount equivalent to prices[1]=4, therefore, the final price you will pay is 8 - 4 = 4. 
For item 1 with price[1]=4 you will receive a discount equivalent to prices[3]=2, therefore, the final price you will pay is 4 - 2 = 2. 
For item 2 with price[2]=6 you will receive a discount equivalent to prices[3]=2, therefore, the final price you will pay is 6 - 2 = 4. 
For items 3 and 4 you will not receive any discount at all.

Example 2:

Input: prices = [1,2,3,4,5]
Output: [1,2,3,4,5]
Explanation: In this case, for all items, you will not receive any discount at all.

Example 3:

Input: prices = [10,1,1,6]
Output: [9,0,1,6]

Constraints:

1 <= prices.length <= 500
1 <= prices[i] <= 10^3

Solution 1: Simulation

Time complexity: O(n^2)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

vector<int> finalPrices(vector<int> prices) {

const int n = prices.size();

for (int i = 0; i < n; ++i)

for (int j = i + 1; j < n; ++j)

if (prices[j] <= prices[i]) {

prices[i] -= prices[j];

break;

}

return prices;

}

};

Solution 2: Monotonic Stack

Use a stack to store monotonically increasing items, when the current item is cheaper than the top of the stack, we get the discount and pop that item. Repeat until the current item is no longer cheaper or the stack becomes empty.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

vector<int> finalPrices(vector<int> prices) {

// stores pointers of monotonically incraseing elements.

stack<int*> s;

for (int& p : prices) {

while (!s.empty() && *s.top() >= p) {

*s.top() -= p;

s.pop();

}

s.push(&p);

}

return prices;

}

};

index version

C++

// Author: Huahua

class Solution {

public:

vector<int> finalPrices(vector<int> prices) {

// stores indices of monotonically incraseing elements.

stack<int> s;

for (int i = 0; i < prices.size(); ++i) {

while (!s.empty() && prices[s.top()] >= prices[i]) {

prices[s.top()] -= prices[i];

s.pop();

}

s.push(i);

}

return prices;

}

};

C++ 11 Smart Pointers 智能指针

By zxi on June 10, 2020

Example code

C++

// Author: Huahua

#include <iostream>

#include <memory>

class Entity {

public:

Entity() { puts("Entity created!"); }

~Entity() { puts("Entity destroyed!"); }

};

void ex1() {

puts("--------");

puts("Entering ex1");

{

puts("Entering ex1::scope1");

auto e1 = std::make_unique<Entity>();

puts("Leaving ex1::scope1");

}

puts("Leaving ex1");

}

void foo(std::unique_ptr<Entity>) {

puts("Entering foo");

puts("Leaving foo");

}

void ex2() {

puts("--------");

puts("Entering ex2");

auto e1 = std::make_unique<Entity>();

foo(std::move(e1));

// e1 was destoried.

puts("Leaving ex2");

}

void ex3() {

puts("--------");

puts("Entering ex3");

auto e1 = std::make_shared<Entity>();

std::cout << e1.use_count() << std::endl;

{

puts("Entering ex3::scope1");

auto e2 = e1; // use_count ++

std::cout << e1.use_count() << std::endl;

auto e3 = std::move(e2); // use_count remains

std::cout << e1.use_count() << std::endl;

puts("Leaving ex3::scope1");

}

std::cout << e1.use_count() << std::endl;

puts("Leaving ex3");

}

void observe(std::weak_ptr<Entity> ew) {

if (std::shared_ptr<Entity> spt = ew.lock()) {

std::cout << spt.use_count() << std::endl;

std::cout << "entity still alive!" << std::endl;

} else {

std::cout << "entity was expired :(" << std::endl;

}

void ex4() {

puts("--------");

puts("Entering ex4");

std::weak_ptr<Entity> ew;

{

puts("Entering ex4::scope1");

auto e1 = std::make_shared<Entity>();

std::cout << e1.use_count() << std::endl;

ew = e1; // use_count remains

std::cout << e1.use_count() << std::endl;

observe(ew);

puts("Leaving ex4::scope1");

}

observe(ew);

puts("Leaving ex4");

}

int main(int argc, char** argv) {

ex1();

ex2();

ex3();

ex4();

return 0;

}

Output

--------

Entering ex1

Entering ex1::scope1

Entity created!

Leaving ex1::scope1

Entity destroyed!

Leaving ex1

--------

Entering ex2

Entity created!

Entering foo

Leaving foo

Entity destroyed!

Leaving ex2

--------

Entering ex3

Entity created!

Entering ex3::scope1

Leaving ex3::scope1

Leaving ex3

Entity destroyed!

--------

Entering ex4

Entering ex4::scope1

Entity created!

entity still alive!

Leaving ex4::scope1

Entity destroyed!

entity was expired :(

Leaving ex4