Posts tagged as “BFS”

花花酱 LeetCode 2045. Second Minimum Time to Reach Destination

By zxi on October 17, 2021

A city is represented as a bi-directional connected graph with n vertices where each vertex is labeled from 1 to n (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [u_i, v_i] denotes a bi-directional edge between vertex u_i and vertex v_i. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself. The time taken to traverse any edge is time minutes.

Each vertex has a traffic signal which changes its color from green to red and vice versa every change minutes. All signals change at the same time. You can enter a vertex at any time, but can leave a vertex only when the signal is green. You cannot wait at a vertex if the signal is green.

The second minimum value is defined as the smallest value strictly larger than the minimum value.

For example the second minimum value of [2, 3, 4] is 3, and the second minimum value of [2, 2, 4] is 4.

Given n, edges, time, and change, return the second minimum time it will take to go from vertex 1 to vertex n.

Notes:

You can go through any vertex any number of times, including 1 and n.
You can assume that when the journey starts, all signals have just turned green.

Example 1:

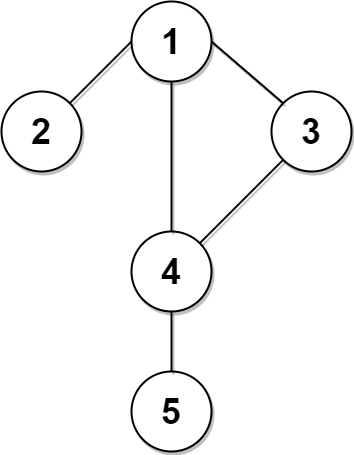
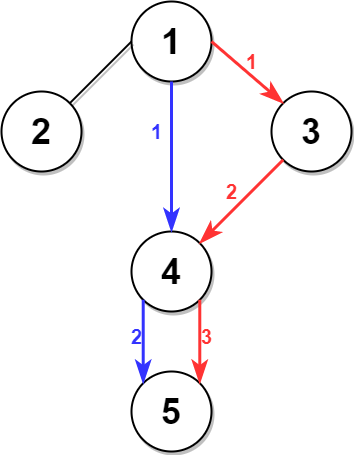
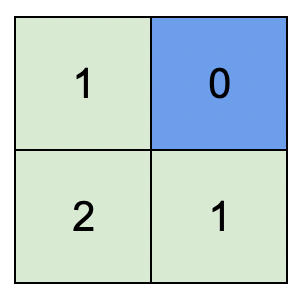
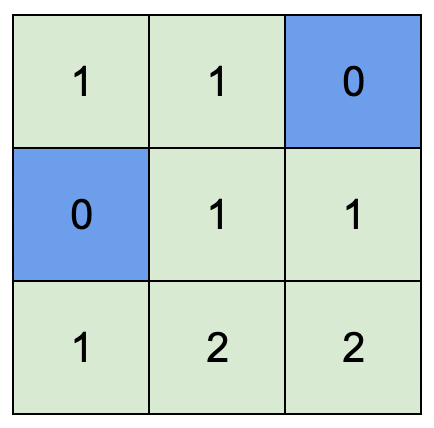
Input: n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
Output: 13
Explanation:
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.

The red path shows the path to get the second minimum time.
- Start at 1, time elapsed=0
- 1 -> 3: 3 minutes, time elapsed=3
- 3 -> 4: 3 minutes, time elapsed=6
- Wait at 4 for 4 minutes, time elapsed=10
- 4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.

Example 2:

Input: n = 2, edges = [[1,2]], time = 3, change = 2
Output: 11
Explanation:
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.

Constraints:

2 <= n <= 10⁴
n - 1 <= edges.length <= min(2 * 10⁴, n * (n - 1) / 2)
edges[i].length == 2
1 <= u_i, v_i <= n
u_i != v_i
There are no duplicate edges.
Each vertex can be reached directly or indirectly from every other vertex.
1 <= time, change <= 10³

Solution: Best first search

Since we’re only looking for second best, to avoid TLE, for each vertex, keep two best time to arrival is sufficient.

Time complexity: O(2ElogE)
Space complexity: O(V+E)

C++

// Author: Huahua

class Solution {

public:

int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {

vector<vector<int>> g(n + 1);

for (const auto& e : edges) {

g[e[0]].push_back(e[1]);

g[e[1]].push_back(e[0]);

}

priority_queue<pair<int, int>> q; // {-t, node}

q.emplace(0, 1);

int min_time = -1;

vector<vector<int>> ts(n + 1);

ts[1].push_back(0);

while (true) {

const int t = -q.top().first;

const int u = q.top().second;

if (u == n) {

if (min_time == -1 || t == min_time) {

min_time = t;

} else {

return t;

}

q.pop();

for (const auto& v : g[u]) {

const int tt = (((t / change) & 1) ? (t + change - t % change) : t) + time;

if ((ts[v].size() > 0 && tt == ts[v].back()) || ts[v].size() >= 2) continue;

ts[v].push_back(tt);

q.emplace(-tt, v);

}

return -1;

}

};

花花酱 LeetCode 1765. Map of Highest Peak

By zxi on February 20, 2021

You are given an integer matrix isWater of size m x n that represents a map of land and water cells.

If isWater[i][j] == 0, cell (i, j) is a land cell.
If isWater[i][j] == 1, cell (i, j) is a water cell.

You must assign each cell a height in a way that follows these rules:

The height of each cell must be non-negative.
If the cell is a water cell, its height must be 0.
Any two adjacent cells must have an absolute height difference of at most 1. A cell is adjacent to another cell if the former is directly north, east, south, or west of the latter (i.e., their sides are touching).

Find an assignment of heights such that the maximum height in the matrix is maximized.

Return an integer matrix height of size m x n where height[i][j] is cell (i, j)‘s height. If there are multiple solutions, return any of them.

Example 1:

Input: isWater = [[0,1],[0,0]]
Output: [[1,0],[2,1]]
Explanation: The image shows the assigned heights of each cell.
The blue cell is the water cell, and the green cells are the land cells.

Example 2:

Input: isWater = [[0,0,1],[1,0,0],[0,0,0]]
Output: [[1,1,0],[0,1,1],[1,2,2]]
Explanation: A height of 2 is the maximum possible height of any assignment.
Any height assignment that has a maximum height of 2 while still meeting the rules will also be accepted.

Constraints:

m == isWater.length
n == isWater[i].length
1 <= m, n <= 1000
isWater[i][j] is 0 or 1.
There is at least one water cell.

Solution: BFS

h[y][x] = min distance of (x, y) to any water cell.

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

// Author: Huahua

class Solution {

public:

vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {

const int m = isWater.size();

const int n = isWater[0].size();

vector<vector<int>> ans(m, vector<int>(n, INT_MIN));

queue<pair<int, int>> q;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

if (isWater[y][x]) {

q.emplace(x, y);

ans[y][x] = 0;

}

const vector<int> dirs{0, -1, 0, 1, 0};

while (!q.empty()) {

const auto [cx, cy] = q.front();

q.pop();

for (int i = 0; i < 4; ++i) {

const int x = cx + dirs[i];

const int y = cy + dirs[i + 1];

if (x < 0 || x >= n || y < 0 || y >= m) continue;

if (ans[y][x] != INT_MIN) continue;

ans[y][x] = ans[cy][cx] + 1;

q.emplace(x, y);

}

return ans;

}

};

花花酱 LeetCode 1654. Minimum Jumps to Reach Home

By zxi on November 14, 2020

A certain bug’s home is on the x-axis at position x. Help them get there from position 0.

The bug jumps according to the following rules:

It can jump exactly a positions forward (to the right).
It can jump exactly b positions backward (to the left).
It cannot jump backward twice in a row.
It cannot jump to any forbidden positions.

The bug may jump forward beyond its home, but it cannot jump to positions numbered with negative integers.

Given an array of integers forbidden, where forbidden[i] means that the bug cannot jump to the position forbidden[i], and integers a, b, and x, return the minimum number of jumps needed for the bug to reach its home. If there is no possible sequence of jumps that lands the bug on position x, return -1.

Example 1:

Input: forbidden = [14,4,18,1,15], a = 3, b = 15, x = 9
Output: 3
Explanation: 3 jumps forward (0 -> 3 -> 6 -> 9) will get the bug home.

Example 2:

Input: forbidden = [8,3,16,6,12,20], a = 15, b = 13, x = 11
Output: -1

Example 3:

Input: forbidden = [1,6,2,14,5,17,4], a = 16, b = 9, x = 7
Output: 2
Explanation: One jump forward (0 -> 16) then one jump backward (16 -> 7) will get the bug home.

Constraints:

1 <= forbidden.length <= 1000
1 <= a, b, forbidden[i] <= 2000
0 <= x <= 2000
All the elements in forbidden are distinct.
Position x is not forbidden.

Solution: BFS

Normal BFS with two tricks:
1. For each position, we need to track whether it’s reached via a forward jump or backward jump
2. How far should we go? If we don’t limit, it can go forever which leads to TLE/MLE. We can limit the distance to 2*max_jump, e.g. 4000, that’s maximum distance we can jump back to home in one shot.

Time complexity: O(max_distance * 2)
Space complexity: O(max_distance * 2)

C++

// Author: Huahua

class Solution {

public:

int minimumJumps(vector<int>& forbidden, int a, int b, int x) {

constexpr int kMaxPosition = 4000;

if (x == 0) return 0;

queue<pair<int, bool>> q{{{0, true}}};

unordered_set<int> seen1, seen2;

for (int f : forbidden) seen1.insert(f), seen2.insert(f);

seen1.insert(0);

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

auto [cur, forward] = q.front(); q.pop();

if (cur == x) return steps;

if (cur > kMaxPosition) continue; // no way to go back

if (seen1.insert(cur + a).second)

q.emplace(cur + a, true);

if (cur - b >= 0 && forward && seen2.insert(cur - b).second)

q.emplace(cur - b, false);

}

++steps;

}

return -1;

}

};

花花酱 LeetCode 1631. Path With Minimum Effort

By zxi on October 24, 2020

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route’s effort is the maximum absolute differencein heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10⁶

Solution: “Lazy BFS / DP”

dp[y][x] = min(max(dp[ty][tx], abs(h[ty][tx] – h[y][x]))) (x, y) and (tx, ty) are neighbors
repeat this process for at most rows * cols times.
if dp does not change after one round which means we found the optimal solution and can break earlier.

Time complexity: O(n^2*m^2))
Space complexity: O(nm)

C++

// Author: Huahua, 824 ms

class Solution {

public:

int minimumEffortPath(vector<vector<int>>& heights) {

const int r = heights.size();

const int c = heights[0].size();

int dp[100][100];

memset(dp, 0x7f, sizeof(dp));

dp[0][0] = 0;

vector<int> dirs{0, -1, 0, 1, 0};

for (int k = 0; k < r * c; ++k) {

bool stable = true;

for (int y = 0; y < r; ++y)

for (int x = 0; x < c; ++x)

for (int d = 0; d < 4; ++d) {

int tx = x + dirs[d];

int ty = y + dirs[d + 1];

if (tx < 0 || tx == c || ty < 0 || ty == r) continue;

int t = max(dp[ty][tx], abs(heights[ty][tx] - heights[y][x]));

if (t < dp[y][x]) {

stable = false;

dp[y][x] = t;

}

if (stable) break;

}

return dp[r - 1][c - 1];

}

};

Solution 2: Binary Search + BFS

Use binary search to guess a cost and then check whether there is path that is under the cost.

Time complexity: O(mn*log(max(h) – min(h)))
Space complexity: O(mn)

C++

// Author: Huahua, 620 ms

class Solution {

public:

int minimumEffortPath(vector<vector<int>>& heights) {

const int rows = heights.size();

const int cols = heights[0].size();

vector<int> dirs{0, -1, 0, 1, 0};

auto bfs = [&](int cost) -> bool {

queue<pair<int, int>> q;

vector<int> seen(cols * rows);

q.emplace(0, 0);

seen[0] = 1;

while (!q.empty()) {

auto [cx, cy] = q.front(); q.pop();

if (cx == cols - 1 && cy == rows - 1) return true;

for (int i = 0; i < 4; ++i) {

int x = cx + dirs[i];

int y = cy + dirs[i + 1];

if (x < 0 || x == cols || y < 0 || y == rows) continue;

if (abs(heights[cy][cx] - heights[y][x]) > cost) continue;

if (seen[y * cols + x]++) continue;

q.emplace(x, y);

}

return false;

};

int l = 0, r = 1e6 + 1;

while (l < r) {

const int m = l + (r - l) / 2;

if (bfs(m)) {

r = m;

} else {

l = m + 1;

}

return l;

}

};

Solution 3: Dijkstra

Time complexity: O(mnlog(mn))
Space complexity: O(mn)

C++

// Author: Huahua, 216 ms

class Solution {

public:

int minimumEffortPath(vector<vector<int>>& heights) {

const vector<int> dirs{0, -1, 0, 1, 0};

const int rows = heights.size();

const int cols = heights[0].size();

using Node = pair<int, int>;

priority_queue<Node, vector<Node>, greater<Node>> q;

vector<int> dist(rows * cols, INT_MAX / 2);

q.emplace(0, 0);

dist[0] = 0;

while (!q.empty()) {

auto [t, u] = q.top(); q.pop();

if (u == rows * cols - 1) return t;

if (t > dist[u]) continue;

const int ux = u % cols;

const int uy = u / cols;

for (int i = 0; i < 4; ++i) {

const int x = ux + dirs[i];

const int y = uy + dirs[i + 1];

if (x < 0 || x == cols || y < 0 || y == rows) continue;

const int v = y * cols + x;

const int c = abs(heights[uy][ux] - heights[y][x]);

if (max(t, c) >= dist[v]) continue;

q.emplace(dist[v] = max(t, c), v);

}

return -1;

}

};

花花酱 LeetCode 1466. Reorder Routes to Make All Paths Lead to the City Zero

By zxi on May 31, 2020

There are n cities numbered from 0 to n-1 and n-1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [a, b] represents a road from city a to b.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It’s guaranteed that each city can reach the city 0 after reorder.

Example 1:

Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3:

Input: n = 3, connections = [[1,0],[2,0]]
Output: 0

Constraints:

2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

Solution: BFS

Augment the graph
g[u][v] = 1, g[v][u] = 0, u->v is an edge in the original graph.

BFS from 0, sum up all the edge costs to visit all the nodes.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int minReorder(int n, vector<vector<int>>& connections) {

vector<vector<pair<int, int>>> g(n); // u -> {v, cost}

for (const auto& e : connections) {

g[e[0]].emplace_back(e[1], 1); // u -> v, needs flip

g[e[1]].emplace_back(e[0], 0); // v -> u, no cost

}

int ans = 0;

queue<int> q{{0}};

vector<int> seen(n);

while (!q.empty()) {

int cur = q.front(); q.pop();

seen[cur] = 1;

for (const auto& [nxt, cost] : g[cur]) {

if (seen[nxt]) continue;

ans += cost;

q.push(nxt);

}

return ans;

}

};