Posts tagged as “bitmask”

花花酱 LeetCode 2405. Optimal Partition of String

By zxi on September 11, 2022

Given a string s, partition the string into one or more substrings such that the characters in each substring are unique. That is, no letter appears in a single substring more than once.

Return the minimum number of substrings in such a partition.

Note that each character should belong to exactly one substring in a partition.

Example 1:

Input: s = "abacaba"
Output: 4
Explanation:
Two possible partitions are ("a","ba","cab","a") and ("ab","a","ca","ba").
It can be shown that 4 is the minimum number of substrings needed.

Example 2:

Input: s = "ssssss"
Output: 6
Explanation:
The only valid partition is ("s","s","s","s","s","s").

Constraints:

1 <= s.length <= 10⁵
s consists of only English lowercase letters.

Solution: Greedy

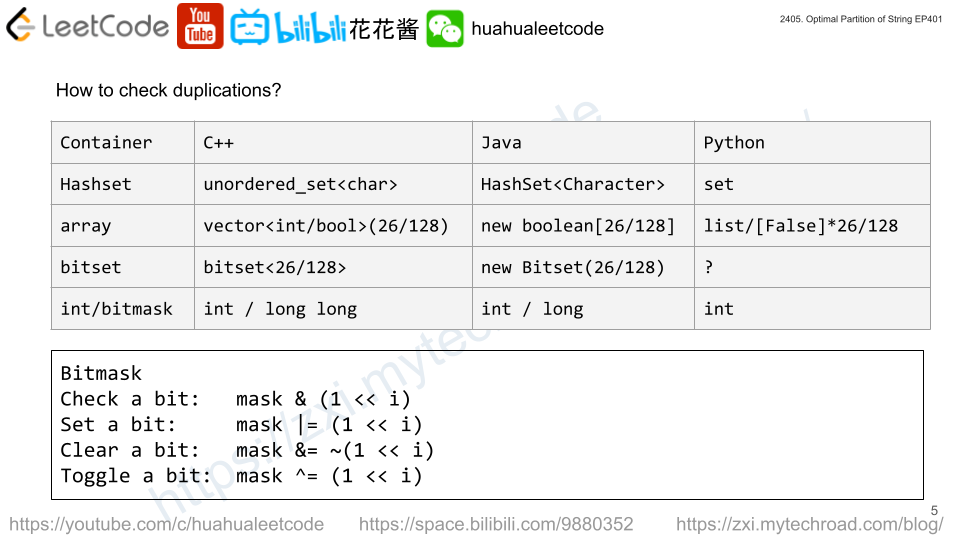
Extend the cur string as long as possible unless a duplicate character occurs.

You can use hashtable / array or bitmask to mark whether a character has been seen so far.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int partitionString(string s) {

unordered_set<char> m;

int ans = 0;

for (char c : s) {

if (m.insert(c).second) continue;

m.clear();

m.insert(c);

++ans;

}

return ans + 1;

}

};

C++

// Author: Huahua

class Solution {

public:

int partitionString(string s) {

vector<int> m(26);

int ans = 0;

for (char c : s) {

if (++m[c - 'a'] == 1) continue;

fill(begin(m), end(m), 0);

m[c - 'a'] = 1;

++ans;

}

return ans + 1;

}

};

C++

// Author: Huahua

class Solution {

public:

int partitionString(string s) {

int mask = 0;

int ans = 0;

for (char c : s) {

if (mask & (1 << (c - 'a'))) {

mask = 0;

++ans;

}

mask |= 1 << (c - 'a');

}

return ans + 1;

}

};

花花酱 LeetCode 2151. Maximum Good People Based on Statements

By zxi on February 4, 2022

There are two types of persons:

The good person: The person who always tells the truth.
The bad person: The person who might tell the truth and might lie.

You are given a 0-indexed 2D integer array statements of size n x n that represents the statements made by n people about each other. More specifically, statements[i][j] could be one of the following:

0 which represents a statement made by person i that person j is a bad person.
1 which represents a statement made by person i that person j is a good person.
2 represents that no statement is made by person i about person j.

Additionally, no person ever makes a statement about themselves. Formally, we have that statements[i][i] = 2 for all 0 <= i < n.

Return the maximum number of people who can be good based on the statements made by the n people.

Example 1:

Input: statements = [[2,1,2],[1,2,2],[2,0,2]]
Output: 2
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is good.
- Person 1 states that person 0 is good.
- Person 2 states that person 1 is bad.
Let's take person 2 as the key.
- Assuming that person 2 is a good person:
- Based on the statement made by person 2, person 1 is a bad person.
- Now we know for sure that person 1 is bad and person 2 is good.
- Based on the statement made by person 1, and since person 1 is bad, they could be:
- telling the truth. There will be a contradiction in this case and this assumption is invalid.
- lying. In this case, person 0 is also a bad person and lied in their statement.
- Following that person 2 is a good person, there will be only one good person in the group.
- Assuming that person 2 is a bad person:
- Based on the statement made by person 2, and since person 2 is bad, they could be:
- telling the truth. Following this scenario, person 0 and 1 are both bad as explained before.
- Following that person 2 is bad but told the truth, there will be no good persons in the group.
- lying. In this case person 1 is a good person.
- Since person 1 is a good person, person 0 is also a good person.
- Following that person 2 is bad and lied, there will be two good persons in the group.
We can see that at most 2 persons are good in the best case, so we return 2.
Note that there is more than one way to arrive at this conclusion.

Example 2:

Input: statements = [[2,0],[0,2]]
Output: 1
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is bad.
- Person 1 states that person 0 is bad.
Let's take person 0 as the key.
- Assuming that person 0 is a good person:
    - Based on the statement made by person 0, person 1 is a bad person and was lying.
    - Following that person 0 is a good person, there will be only one good person in the group.
- Assuming that person 0 is a bad person:
    - Based on the statement made by person 0, and since person 0 is bad, they could be:
        - telling the truth. Following this scenario, person 0 and 1 are both bad.
            - Following that person 0 is bad but told the truth, there will be no good persons in the group.
        - lying. In this case person 1 is a good person.
            - Following that person 0 is bad and lied, there will be only one good person in the group.
We can see that at most, one person is good in the best case, so we return 1.
Note that there is more than one way to arrive at this conclusion.

Constraints:

n == statements.length == statements[i].length
2 <= n <= 15
statements[i][j] is either 0, 1, or 2.
statements[i][i] == 2

Solution: Combination / Bitmask

Enumerate all subsets of n people and assume they are good people. Check whether their statements have any conflicts. We can ignore the statements from bad people since those can be either true or false and does not affect our checks.

Time complexity: O(n²2ⁿ)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int maximumGood(vector<vector<int>>& statements) {

const int n = statements.size();

auto valid = [&](int s) {

for (int i = 0; i < n; ++i) {

if (!(s >> i & 1)) continue;

for (int j = 0; j < n; ++j) {

const bool good = s >> j & 1;

if ((good && statements[i][j] == 0) || (!good && statements[i][j] == 1))

return false;

}

return true;

};

int ans = 0;

for (int s = 1; s < 1 << n; ++s)

if (valid(s)) ans = max(ans, __builtin_popcount(s));

return ans;

}

};

花花酱 LeetCode 2135. Count Words Obtained After Adding a Letter

By zxi on January 17, 2022

You are given two 0-indexed arrays of strings startWords and targetWords. Each string consists of lowercase English letters only.

For each string in targetWords, check if it is possible to choose a string from startWords and perform a conversion operation on it to be equal to that from targetWords.

The conversion operation is described in the following two steps:

Append any lowercase letter that is not present in the string to its end.
- For example, if the string is "abc", the letters 'd', 'e', or 'y' can be added to it, but not 'a'. If 'd' is added, the resulting string will be "abcd".
Rearrange the letters of the new string in any arbitrary order.
- For example, "abcd" can be rearranged to "acbd", "bacd", "cbda", and so on. Note that it can also be rearranged to "abcd" itself.

Return the number of strings in targetWords that can be obtained by performing the operations on any string of startWords.

Note that you will only be verifying if the string in targetWords can be obtained from a string in startWords by performing the operations. The strings in startWords do not actually change during this process.

Example 1:

Input: startWords = ["ant","act","tack"], targetWords = ["tack","act","acti"]
Output: 2
Explanation:
- In order to form targetWords[0] = "tack", we use startWords[1] = "act", append 'k' to it, and rearrange "actk" to "tack".
- There is no string in startWords that can be used to obtain targetWords[1] = "act".
  Note that "act" does exist in startWords, but we must append one letter to the string before rearranging it.
- In order to form targetWords[2] = "acti", we use startWords[1] = "act", append 'i' to it, and rearrange "acti" to "acti" itself.

Example 2:

Input: startWords = ["ab","a"], targetWords = ["abc","abcd"]
Output: 1
Explanation:
- In order to form targetWords[0] = "abc", we use startWords[0] = "ab", add 'c' to it, and rearrange it to "abc".
- There is no string in startWords that can be used to obtain targetWords[1] = "abcd".

Constraints:

1 <= startWords.length, targetWords.length <= 5 * 10⁴
1 <= startWords[i].length, targetWords[j].length <= 26
Each string of startWords and targetWords consists of lowercase English letters only.
No letter occurs more than once in any string of startWords or targetWords.

Solution: Bitmask w/ Hashtable

Since there is no duplicate letters in each word, we can use a bitmask to represent a word.

Step 1: For each word in startWords, we obtain its bitmask and insert it into a hashtable.
Step 2: For each word in targetWords, enumerate it’s letter and unset 1 bit (skip one letter) and see whether it’s in the hashtable or not.

E.g. for target word “abc”, its bitmask is 0…0111, and we test whether “ab” or “ac” or “bc” in the hashtable or not.

Time complexity: O(n * 26^2)
Space complexity: O(n * 26)

C++

// Author: Huahua

class Solution {

public:

int wordCount(vector<string>& startWords, vector<string>& targetWords) {

unordered_set<int> s;

auto getKey = [](const string& s) {

return accumulate(begin(s), end(s), 0, [](int key, char c) { return key | (1 << (c - 'a')); });

};

for (const string& w : startWords)

s.insert(getKey(w));

return accumulate(begin(targetWords), end(targetWords), 0, [&](int ans, const string& w) {

const int key = getKey(w);

return ans + any_of(begin(w), end(w), [&](char c) { return s.count(key ^ (1 << (c - 'a'))); });

});

}

};

花花酱 LeetCode 1915. Number of Wonderful Substrings

By zxi on December 25, 2021

A wonderful string is a string where at most one letter appears an odd number of times.

For example, "ccjjc" and "abab" are wonderful, but "ab" is not.

Given a string word that consists of the first ten lowercase English letters ('a' through 'j'), return the number of wonderful non-empty substrings in word. If the same substring appears multiple times in word, then count each occurrence separately.

A substring is a contiguous sequence of characters in a string.

Example 1:

Input: word = "aba"
Output: 4
Explanation: The four wonderful substrings are underlined below:
- "aba" -> "a"
- "aba" -> "b"
- "aba" -> "a"
- "aba" -> "aba"

Example 2:

Input: word = "aabb"
Output: 9
Explanation: The nine wonderful substrings are underlined below:
- "aabb" -> "a"
- "aabb" -> "aa"
- "aabb" -> "aab"
- "aabb" -> "aabb"
- "aabb" -> "a"
- "aabb" -> "abb"
- "aabb" -> "b"
- "aabb" -> "bb"
- "aabb" -> "b"

Example 3:

Input: word = "he"
Output: 2
Explanation: The two wonderful substrings are underlined below:
- "he" -> "h"
- "he" -> "e"

Constraints:

1 <= word.length <= 10⁵
word consists of lowercase English letters from 'a' to 'j'.

Solution: Prefix Bitmask + Hashtable

Similar to 花花酱 LeetCode 1371. Find the Longest Substring Containing Vowels in Even Counts, we use a bitmask to represent the occurrence (odd or even) of each letter and use a hashtable to store the frequency of each bitmask seen so far.

1. “0000000000” means all letters occur even times.
2. “0000000101” means all letters occur even times expect letter ‘a’ and ‘c’ that occur odd times.

We scan the word from left to right and update the bitmask: bitmask ^= (1 << (c-‘a’)).
However, the bitmask only represents the state of the prefix, i.e. word[0:i], then how can we count substrings? The answer is hashtable. If the same bitmask occurs c times before, which means there are c indices that word[0~j1], word[0~j2], …, word[0~jc] have the same state as word[0~i] that means for word[j1+1~i], word[j2+1~i], …, word[jc+1~i], all letters occurred even times.
For the “at most one odd” case, we toggle each bit of the bitmask and check how many times it occurred before.

ans += freq[mask] + sum(freq[mask ^ (1 << i)] for i in range(k))

Time complexity: O(n*k)
Space complexity: O(2^k)
where k = j – a + 1 = 10

C++

// Author: Huahua

class Solution {

public:

long long wonderfulSubstrings(string word) {

constexpr int l = 'j' - 'a' + 1;

vector<int> count(1 << l);

count[0] = 1;

int mask = 0;

long long ans = 0;

for (char c : word) {

mask ^= 1 << (c - 'a');

for (int i = 0; i < l; ++i)

ans += count[mask ^ (1 << i)]; // one odd.

ans += count[mask]++; // all even.

}

return ans;

}

};

花花酱 LeetCode 1900. The Earliest and Latest Rounds Where Players Compete

By zxi on August 11, 2021

There is a tournament where n players are participating. The players are standing in a single row and are numbered from 1 to n based on their initial standing position (player 1 is the first player in the row, player 2 is the second player in the row, etc.).

The tournament consists of multiple rounds (starting from round number 1). In each round, the i^th player from the front of the row competes against the i^th player from the end of the row, and the winner advances to the next round. When the number of players is odd for the current round, the player in the middle automatically advances to the next round.

For example, if the row consists of players 1, 2, 4, 6, 7
- Player 1 competes against player 7.
- Player 2 competes against player 6.
- Player 4 automatically advances to the next round.

After each round is over, the winners are lined back up in the row based on the original ordering assigned to them initially (ascending order).

The players numbered firstPlayer and secondPlayer are the best in the tournament. They can win against any other player before they compete against each other. If any two other players compete against each other, either of them might win, and thus you may choose the outcome of this round.

Given the integers n, firstPlayer, and secondPlayer, return an integer array containing two values, the earliest possible round number and the latest possible round number in which these two players will compete against each other, respectively.

Example 1:

Input: n = 11, firstPlayer = 2, secondPlayer = 4
Output: [3,4]
Explanation:
One possible scenario which leads to the earliest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 2, 3, 4, 5, 6, 11
Third round: 2, 3, 4
One possible scenario which leads to the latest round number:
First round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Second round: 1, 2, 3, 4, 5, 6
Third round: 1, 2, 4
Fourth round: 2, 4

Example 2:

Input: n = 5, firstPlayer = 1, secondPlayer = 5
Output: [1,1]
Explanation: The players numbered 1 and 5 compete in the first round.
There is no way to make them compete in any other round.

Constraints:

2 <= n <= 28
1 <= firstPlayer < secondPlayer <= n

Solution 1: Simulation using recursion

All possible paths,
Time complexity: O(n²*2ⁿ)
Space complexity: O(logn)

dfs(s, i, j, d) := let i battle with j at round d, given s (binary mask of dead players).

C++

// Author: Huahua

class Solution {

public:

vector<int> earliestAndLatest(int n, int a, int b) {

vector<int> ans{INT_MAX, INT_MIN};

function<void(int, int, int, int)> dfs = [&](int s, int i, int j, int d) {

while (i < j && s >> i & 1) ++i;

while (i < j && s >> j & 1) --j;

if (i >= j) {

return dfs(s, 1, n, d + 1);

} else if (i == a && j == b) {

ans[0] = min(ans[0], d);

ans[1] = max(ans[1], d);

} else {

if (i != a && i != b)

dfs(s | (1 << i), i + 1, j - 1, d);

if (j != a && j != b)

dfs(s | (1 << j), i + 1, j - 1, d);

}

};

dfs(0, 1, n, 1);

return ans;

}

};