花花酱 LeetCode 1110. Delete Nodes And Return Forest

By zxi on August 8, 2019

Given the root of a binary tree, each node in the tree has a distinct value.

After deleting all nodes with a value in to_delete, we are left with a forest (a disjoint union of trees).

Return the roots of the trees in the remaining forest. You may return the result in any order.

Example 1:

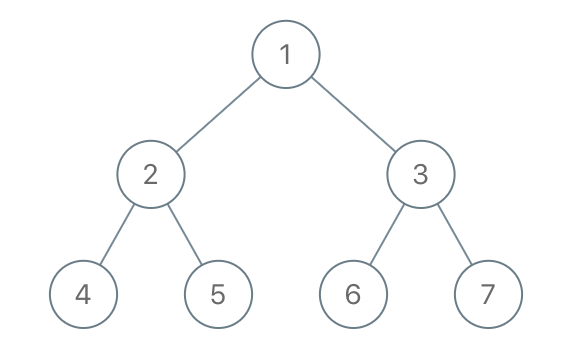
Input: root = [1,2,3,4,5,6,7], to_delete = [3,5]
Output: [[1,2,null,4],[6],[7]]

Constraints:

The number of nodes in the given tree is at most 1000.
Each node has a distinct value between 1 and 1000.
to_delete.length <= 1000
to_delete contains distinct values between 1 and 1000.

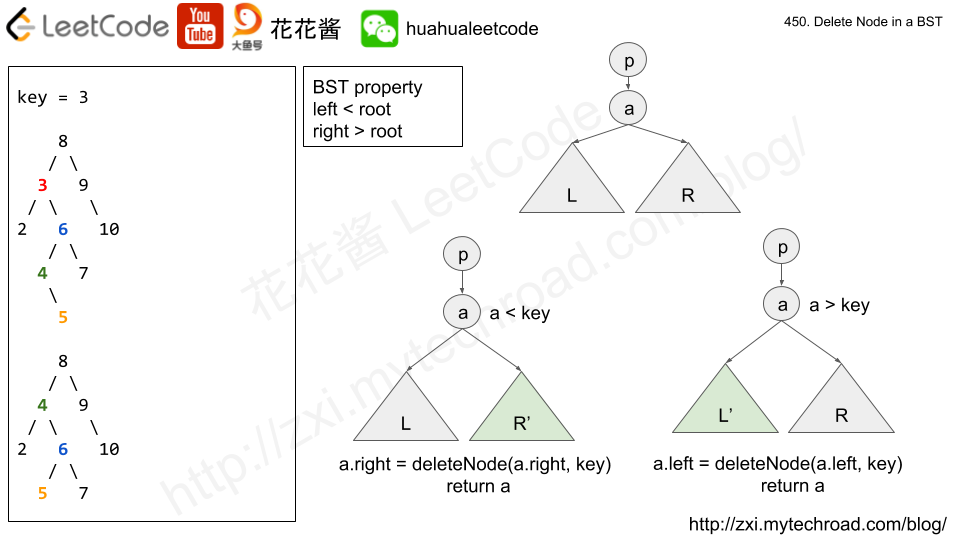
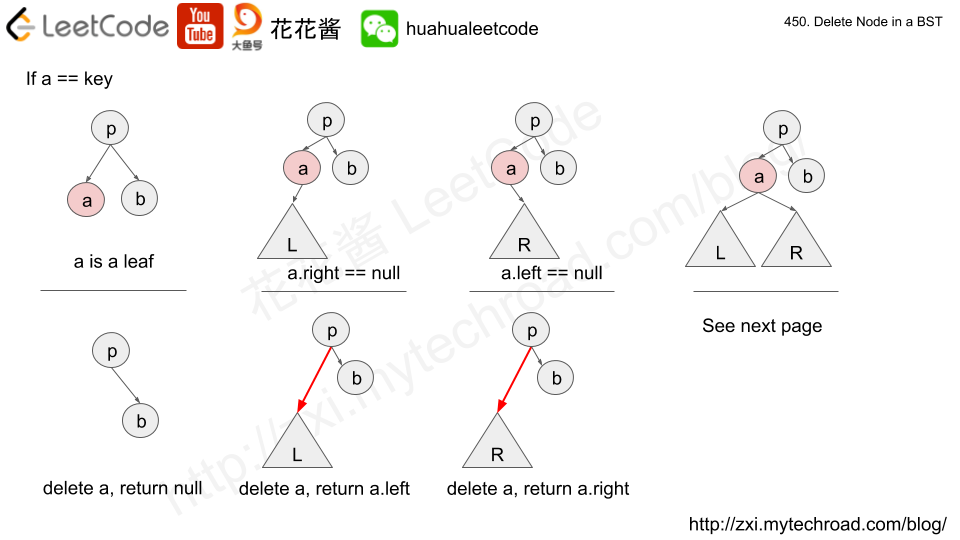
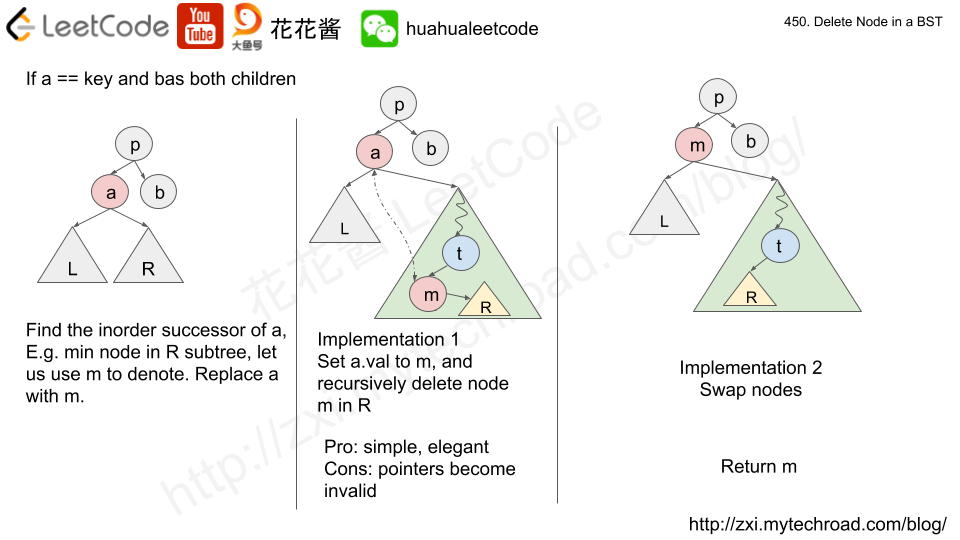
Solution: Recursion / Post-order traversal

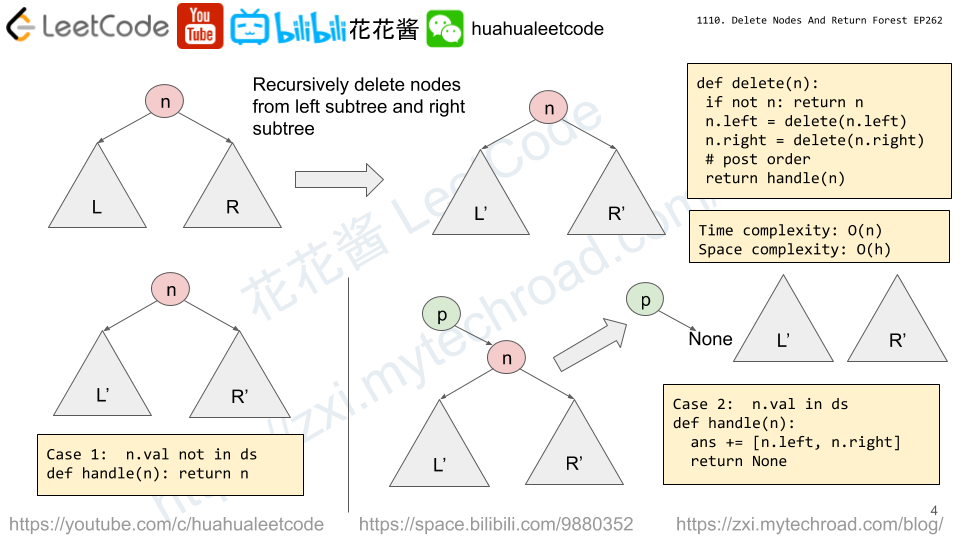
Recursively delete nodes on left subtree and right subtree and return the trimmed tree.
if the current node needs to be deleted, then its non-null children will be added to output array.

Time complexity: O(n)
Space complexity: O(|d| + h)

C++

// Author: Huahua

class Solution {

public:

vector<TreeNode*> delNodes(TreeNode* root, vector<int>& to_delete) {

vector<TreeNode*> ans;

unordered_set<int> s{begin(to_delete), end(to_delete)};

function<TreeNode*(TreeNode*)> del = [&](TreeNode* n) -> TreeNode* {

if (!n) return nullptr;

if (n->left) n->left = del(n->left);

if (n->right) n->right = del(n->right);

if (!s.count(n->val)) return n;

if (n->left) ans.push_back(n->left);

if (n->right) ans.push_back(n->right);

return nullptr;

};

TreeNode* r = del(root);

if (r) ans.push_back(r);

return ans;

}

};

Python3

# Author: Huahua

class Solution:

def delNodes(self, root: TreeNode, to_delete: List[int]) -> List[TreeNode]:

ans = []

ds = set(to_delete)

def process(n):

if not n: return None

n.left, n.right = process(n.left), process(n.right)

if n.val not in ds: return n

if n.left: ans.append(n.left)

if n.right: ans.append(n.right)

return None

root = process(root)

if root: ans.append(root)

return ans

花花酱 LeetCode 712. Minimum ASCII Delete Sum for Two Strings

By zxi on July 20, 2018

Problem

Given two strings s1, s2, find the lowest ASCII sum of deleted characters to make two strings equal.

Example 1:

Input: s1 = "sea", s2 = "eat"
Output: 231
Explanation: Deleting "s" from "sea" adds the ASCII value of "s" (115) to the sum.
Deleting "t" from "eat" adds 116 to the sum.
At the end, both strings are equal, and 115 + 116 = 231 is the minimum sum possible to achieve this.

Example 2:

Input: s1 = "delete", s2 = "leet"
Output: 403
Explanation: Deleting "dee" from "delete" to turn the string into "let",
adds 100[d]+101[e]+101[e] to the sum.  Deleting "e" from "leet" adds 101[e] to the sum.
At the end, both strings are equal to "let", and the answer is 100+101+101+101 = 403.
If instead we turned both strings into "lee" or "eet", we would get answers of 433 or 417, which are higher.

Note:

0 < s1.length, s2.length <= 1000.
All elements of each string will have an ASCII value in [97, 122].

Solution: DP

Time complexity: O(l1 * l2)

Space complexity: O(l1 * l2)

C++

// Author: Huahua

// Running time: 8 ms

class Solution {

public:

int minimumDeleteSum(string s1, string s2) {

const int l1 = s1.length();

const int l2 = s2.length();

// dp[i][j] := min delete sum of (s1.substr(0, i), s2.substr(0, j))

vector<vector<int>> dp(l1 + 1, vector<int>(l2 + 1));

for (int i = 1; i <= l1; ++i)

dp[i][0] = dp[i - 1][0] + s1[i - 1];

for (int j = 1; j <= l2; ++j)

dp[0][j] = dp[0][j - 1] + s2[j - 1];

for (int i = 1; i <= l1; ++i)

for (int j = 1; j <= l2; ++j)

if (s1[i - 1] == s2[j - 1])

// keep s1[i - 1] and s2[j - 1]

dp[i][j] = dp[i - 1][j - 1];

else

dp[i][j] = min(dp[i - 1][j] + s1[i - 1], // delete s1[i - 1]

dp[i][j - 1] + s2[j - 1]); // delete s2[j - 1]

return dp[l1][l2];

}

};

Solution2: Recursion + Memorization

Time complexity: O(l1 * l2)

Space complexity: O(l1 * l2)

C++

// Author: Huahua

// Running time: 20 ms

class Solution {

public:

int minimumDeleteSum(string s1, string s2) {

const int l1 = s1.length();

const int l2 = s2.length();

m_ = vector<vector<int>>(l1 + 1, vector<int>(l2 + 1, INT_MAX));

return dp(s1, l1, s2, l2);

}

private:

int dp(const string& s1, int i, const string& s2, int j) {

if (i == 0 && j == 0) return 0;

if (m_[i][j] != INT_MAX) return m_[i][j];

if (i == 0) // s1 is empty.

return m_[i][j] = dp(s1, i, s2, j - 1) + s2[j - 1];

if (j == 0) // s2 is empty

return m_[i][j] = dp(s1, i - 1, s2, j) + s1[i - 1];

if (s1[i - 1] == s2[j - 1]) // skip s1[i-1] / s2[j-1]

return m_[i][j] = dp(s1, i - 1, s2, j - 1);

return m_[i][j] = min(dp(s1, i - 1, s2, j) + s1[i - 1], // del s1[i-1]

dp(s1, i, s2, j - 1) + s2[j - 1]); // del s2[j-1]

}

vector<vector<int>> m_;

};

Problem

https://leetcode.com/problems/delete-node-in-a-bst/description/

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

Search for a node to remove.
If the node is found, delete the node.

Note: Time complexity should be O(height of tree).

Example:

root = [5,3,6,2,4,null,7]
key = 3

    5
   / \
  3   6
 / \   \
2   4   7

Given key to delete is 3. So we find the node with value 3 and delete it.

One valid answer is [5,4,6,2,null,null,7], shown in the following BST.

    5
   / \
  4   6
 /     \
2       7

Another valid answer is [5,2,6,null,4,null,7].

    5
   / \
  2   6
   \   \
    4   7

Solution: Recursion

Time complexity: O(h)

Space complexity: O(h)

C++

// Author: Huahua

// Running time: 36 ms

/**

* Definition for a binary tree node.

* struct TreeNode {

* int val;

* TreeNode *left;

* TreeNode *right;

* TreeNode(int x) : val(x), left(NULL), right(NULL) {}

* };

class Solution {

public:

TreeNode* deleteNode(TreeNode* root, int key) {

if (root == nullptr) return root;

if (key > root->val) {

root->right = deleteNode(root->right, key);

} else if (key < root->val) {

root->left = deleteNode(root->left, key);

} else {

TreeNode* new_root = nullptr;

if (root->left == nullptr) {

new_root = root->right;

} else if (root->right == nullptr) {

new_root = root->left;

} else {

// Find the min node in the right sub tree

TreeNode* parent = root;

new_root = root->right;

while (new_root->left != nullptr) {

parent = new_root;

new_root = new_root->left;

}

if (parent != root) {

parent->left = new_root->right;

new_root->right = root->right;

}

new_root->left = root->left;

}

delete root;

return new_root;

}

return root;

}

};

// Author: Huahua

// Running time: 35 ms

class Solution {

public:

TreeNode* deleteNode(TreeNode* root, int key) {

if (root == nullptr) return root;

if (key > root->val) {

root->right = deleteNode(root->right, key);

} else if (key < root->val) {

root->left = deleteNode(root->left, key);

} else {

if (root->left != nullptr && root->right != nullptr) {

TreeNode* min = root->right;

while (min->left != nullptr) min = min->left;

root->val = min->val;

root->right = deleteNode(root->right, min->val);

} else {

TreeNode* new_root = root->left == nullptr ? root->right : root->left;

root->left = root->right = nullptr;

delete root;

return new_root;

}

return root;

}

};

Posts tagged as “delete”

花花酱 LeetCode 1110. Delete Nodes And Return Forest

Solution: Recursion / Post-order traversal

C++

Python3

花花酱 LeetCode 712. Minimum ASCII Delete Sum for Two Strings

Problem

Solution: DP

Solution2: Recursion + Memorization

Related Problems

花花酱 LeetCode 450. Delete Node in a BST

Problem

Solution: Recursion