花花酱 LeetCode 2316. Count Unreachable Pairs of Nodes in an Undirected Graph

You are given an integer n. There is an undirected graph with n nodes, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

Return the number of pairs of different nodes that are unreachable from each other.

Example 1:

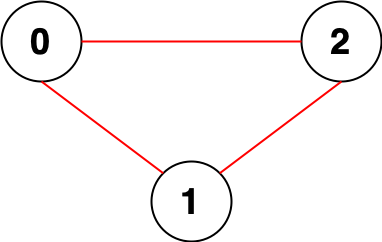
Input: n = 3, edges = [[0,1],[0,2],[1,2]]
Output: 0
Explanation: There are no pairs of nodes that are unreachable from each other. Therefore, we return 0.

Example 2:

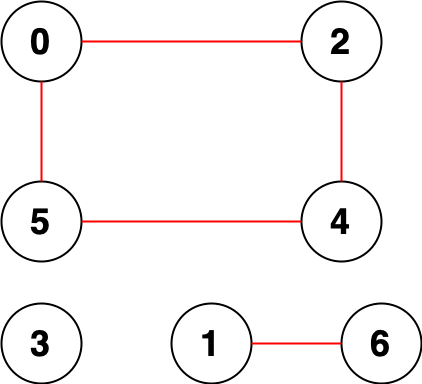
Input: n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
Output: 14
Explanation: There are 14 pairs of nodes that are unreachable from each other:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]].
Therefore, we return 14.

Constraints:

• 1 <= n <= 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• There are no repeated edges.

Solution 1: DFS

Use DFS to find all CCs

Time complexity: O(V+E)
Space complexity: O(V+E)

Solution 2: Union Find

Time complexity: O(V+E)
Space complexity: O(V)