Posts tagged as “DFS”

花花酱 LeetCode 1263. Minimum Moves to Move a Box to Their Target Location

By zxi on November 26, 2019

Storekeeper is a game in which the player pushes boxes around in a warehouse trying to get them to target locations.

The game is represented by a grid of size n*m, where each element is a wall, floor, or a box.

Your task is move the box 'B' to the target position 'T' under the following rules:

Player is represented by character 'S' and can move up, down, left, right in the grid if it is a floor (empy cell).
Floor is represented by character '.' that means free cell to walk.
Wall is represented by character '#' that means obstacle (impossible to walk there).
There is only one box 'B' and one target cell 'T' in the grid.
The box can be moved to an adjacent free cell by standing next to the box and then moving in the direction of the box. This is a push.
The player cannot walk through the box.

Return the minimum number of pushes to move the box to the target. If there is no way to reach the target, return -1.

Example 1:

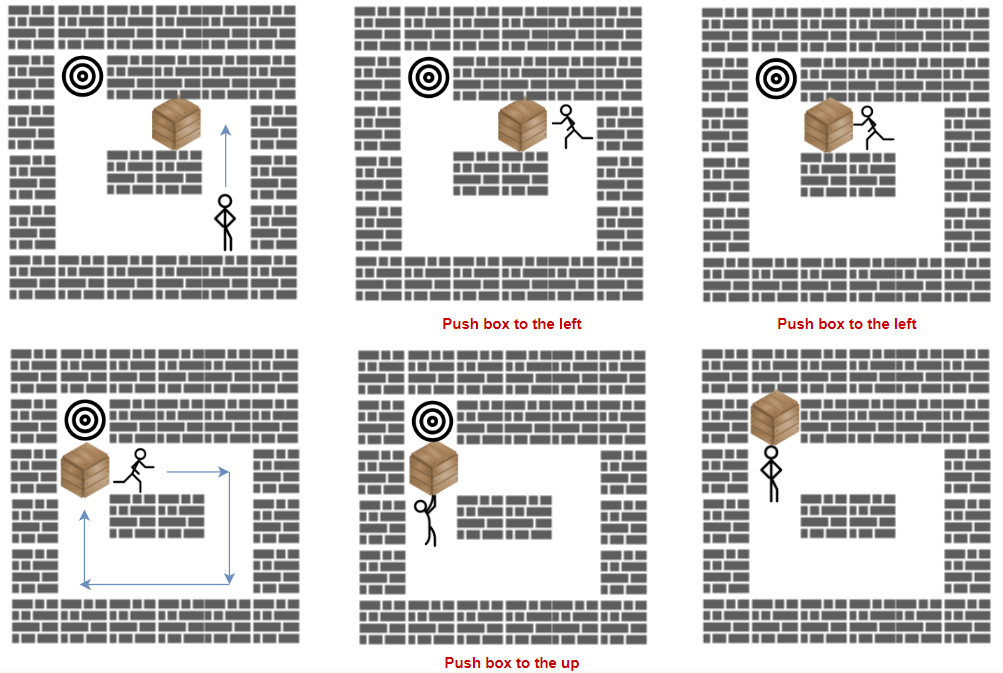
Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#",".","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 3
Explanation: We return only the number of times the box is pushed.

Example 2:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T","#","#","#","#"],
               ["#",".",".","B",".","#"],
               ["#","#","#","#",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: -1

Example 3:

Input: grid = [["#","#","#","#","#","#"],
               ["#","T",".",".","#","#"],
               ["#",".","#","B",".","#"],
               ["#",".",".",".",".","#"],
               ["#",".",".",".","S","#"],
               ["#","#","#","#","#","#"]]
Output: 5
Explanation:  push the box down, left, left, up and up.

Example 4:

Input: grid = [["#","#","#","#","#","#","#"],
               ["#","S","#",".","B","T","#"],
               ["#","#","#","#","#","#","#"]]
Output: -1

Constraints:

1 <= grid.length <= 20
1 <= grid[i].length <= 20
grid contains only characters '.', '#', 'S' , 'T', or 'B'.
There is only one character 'S', 'B' and 'T' in the grid.

Solution: BFS + DFS

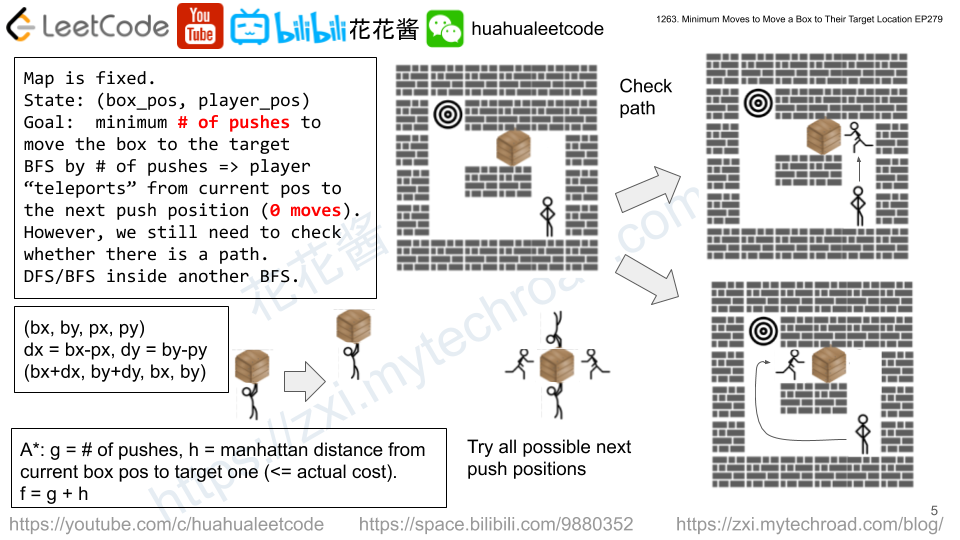
BFS to search by push steps to find miminal number of pushes. Each time we move from the previous position (initial position or last push position) to a new push position. Use DFS to check that whether that path exist or not.

C++

// Author: Huahua

struct Node {

int bx;

int by;

int px;

int py;

int key() const { return ((by * 20 + bx) << 16) | (py * 20 + px); }

};

class Solution {

public:

int minPushBox(vector<vector<char>>& grid) {

const int n = grid.size();

const int m = grid[0].size();

Node start;

Node end;

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x)

if (grid[y][x] == 'B') {

start.bx = x;

start.by = y;

} else if (grid[y][x] == 'S') {

start.px = x;

start.py = y;

} else if (grid[y][x] == 'T') {

end.bx = x;

end.by = y;

}

auto hasPath = [&](const Node& cur, int tx, int ty) {

vector<int> seen(m*n);

function<bool(int, int)> dfs = [&](int x, int y) {

if (x < 0 || x >= m || y < 0 || y >= n || grid[y][x] == '#')

return false;

if (x == cur.bx && y == cur.by) return false;

int key = y * m + x;

if (seen[key]) return false;

seen[key] = 1;

if (x == tx && y == ty) return true;

return dfs(x + 1, y) || dfs(x - 1, y) || dfs(x, y + 1) || dfs(x, y - 1);

};

return dfs(cur.px, cur.py);

};

auto canPush = [&](const Node& cur, int dx, int dy, Node* nxt) {

const int bx = cur.bx + dx;

const int by = cur.by + dy;

if (bx < 0 || bx >= m || by < 0 || by >= n || grid[by][bx] == '#')

return false;

if (!hasPath(cur, cur.bx - dx, cur.by - dy)) return false;

nxt->bx = bx;

nxt->by = by;

nxt->px = cur.bx;

nxt->py = cur.by;

return true;

};

const vector<int> dirs{0, -1, 0, 1, 0};

unordered_set<int> seen;

queue<Node> q;

q.push(start);

int steps = 0;

while (q.size()) {

int size = q.size();

while (size--) {

Node cur = q.front();

q.pop();

for (int i = 0; i < 4; ++i) {

Node nxt;

if (!canPush(cur, dirs[i], dirs[i + 1], &nxt) ||

seen.count(nxt.key()))

continue;

if (nxt.bx == end.bx && nxt.by == end.by) return steps + 1;

seen.insert(nxt.key());

q.push(nxt);

}

++steps;

}

return -1;

}

};

**Solution: A* + BFS**

g : history = # of pushes
h: heuristics = Manhattan distance from the current box position to the target position, always <= actual moves.
f = g + h

C++

100

101

// Author: Huahua, 4 ms, 17.5 MB

struct Node {

int bx;

int by;

int px;

int py;

int h;

int g;

int key() const {

return ((by * m + bx) << 2) | ((bx - px) + 1) | ((by - py) + 1) >> 1;

}

int f() const { return g + h; }

bool operator< (const Node& o) const {

return f() > o.f();

}

static int m;

};

int Node::m;

class Solution {

public:

int minPushBox(vector<vector<char>>& grid) {

const vector<int> dirs{0, -1, 0, 1, 0};

const int n = grid.size();

const int m = Node::m = grid[0].size();

Node start;

Node end;

for (int y = 0; y < n; ++y)

for (int x = 0; x < m; ++x)

if (grid[y][x] == 'B') {

start.bx = x;

start.by = y;

} else if (grid[y][x] == 'S') {

start.px = x;

start.py = y;

} else if (grid[y][x] == 'T') {

end.bx = x;

end.by = y;

}

auto isValid = [&](int x, int y) {

return !(x < 0 || x >= m || y < 0 || y >= n || grid[y][x] == '#');

};

auto hasPath = [&](const Node& cur, int tx, int ty) {

if (!isValid(tx, ty)) return false;

vector<int> seen(m*n);

queue<int> q;

q.push(cur.py * m + cur.px);

seen[cur.py * m + cur.px] = 1;

while (q.size()) {

int x = q.front() % m;

int y = q.front() / m;

q.pop();

for (int i = 0; i < 4; ++i) {

int nx = x + dirs[i];

int ny = y + dirs[i + 1];

if (!isValid(nx, ny)) continue;

if (nx == cur.bx && ny == cur.by) continue;

if (nx == tx && ny == ty) return true;

if (seen[ny * m + nx]++) continue;

q.push(ny * m + nx);

}

return false;

};

auto canPush = [&](const Node& cur, int dx, int dy, Node* nxt) {

nxt->bx = cur.bx + dx;

nxt->by = cur.by + dy;

nxt->px = cur.bx;

nxt->py = cur.by;

nxt->g = cur.g + 1;

nxt->h = abs(nxt->bx - end.bx) + abs(nxt->by - end.by);

if (!isValid(nxt->bx, nxt->by)) return false;

return hasPath(cur, cur.bx - dx, cur.by - dy);

};

vector<int> seen(m*n*4);

priority_queue<Node> q;

start.g = 0;

start.h = abs(start.bx - end.bx) + abs(start.by - end.by);

q.push(start);

while (q.size()) {

Node cur = q.top();

q.pop();

for (int i = 0; i < 4; ++i) {

Node nxt;

if (!canPush(cur, dirs[i], dirs[i + 1], &nxt) || seen[nxt.key()]++) continue;

if (nxt.bx == end.bx && nxt.by == end.by) return nxt.g;

q.push(nxt);

}

return -1;

}

};

花花酱 LeetCode 1254. Number of Closed Islands

By zxi on November 9, 2019

Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

Example 1:

Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

Constraints:

1 <= grid.length, grid[0].length <= 100
0 <= grid[i][j] <=1

Solution: DFS/Backtracking

For each connected component, if it can reach the boundary then it’s not a closed island.

Time complexity: O(n*m)
Space complexity: O(n*m)

C++

// Author: Huahua

class Solution {

public:

int closedIsland(vector<vector<int>>& grid) {

const int n = grid.size();

const int m = grid[0].size();

function<int(int, int)> dfs = [&](int x, int y) {

if (x < 0 || y < 0 || x >= m || y >= n) return 0;

if (grid[y][x]++) return 1;

return dfs(x + 1, y) & dfs(x - 1, y) & dfs(x, y + 1) & dfs(x, y - 1);

};

int ans = 0;

for (int i = 0; i < n; ++i)

for (int j = 0; j < m; ++j)

if (!grid[i][j]) ans += dfs(j, i);

return ans;

}

};

花花酱 LeetCode 1239. Maximum Length of a Concatenated String with Unique Characters

By zxi on October 27, 2019

Given an array of strings arr. String s is a concatenation of a sub-sequence of arr which have unique characters.

Return the maximum possible length of s.

Example 1:

Input: arr = ["un","iq","ue"]
Output: 4
Explanation: All possible concatenations are "","un","iq","ue","uniq" and "ique".
Maximum length is 4.

Example 2:

Input: arr = ["cha","r","act","ers"]
Output: 6
Explanation: Possible solutions are "chaers" and "acters".

Example 3:

Input: arr = ["abcdefghijklmnopqrstuvwxyz"]
Output: 26

Constraints:

1 <= arr.length <= 16
1 <= arr[i].length <= 26
arr[i] contains only lower case English letters.

Solution: Combination + Bit

Time complexity: O(2^n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maxLength(vector<string>& arr) {

vector<int> a;

for (const string& x : arr) {

set<char> s(begin(x), end(x));

if (s.size() != x.length()) continue;

a.push_back(0);

for (char c : x) a.back() |= 1 << (c - 'a');

}

int ans = 0;

function<void(int, int)> dfs = [&](int s, int cur) {

ans = max(ans, __builtin_popcount(cur));

for (int i = s; i < a.size(); ++i)

if ((cur & a[i]) == 0)

dfs(i + 1, cur | a[i]);

};

dfs(0, 0);

return ans;

}

};

Solution 2: DP

Time complexity: O(2^n)
Space complexity: O(2^n)

C++

// Author: Huahua

class Solution {

public:

int maxLength(vector<string>& arr) {

vector<int> a;

for (const string& x : arr) {

int mask = 0;

for (char c : x) mask |= 1 << (c - 'a');

if (__builtin_popcount(mask) != x.length()) continue;

a.push_back(mask);

}

int ans = 0;

vector<int> dp{0};

for (int i = 0; i < a.size(); ++i) {

int size = dp.size();

for (int j = 0; j < size; ++j) {

if (dp[j] & a[i]) continue;

int t = dp[j] | a[i];

dp.push_back(t);

ans = max(ans, __builtin_popcount(t));

}

return ans;

}

};

花花酱 LeetCode 131. Palindrome Partitioning

By zxi on October 10, 2019

Given a string s, partition s such that every substring of the partition is a palindrome.

Return all possible palindrome partitioning of s.

Example:

Input: "aab"
Output:
[
  ["aa","b"],
  ["a","a","b"]
]

Solution1: DP

dp[i] := ans of str[0:i]
dp[j] = { x + str[i:len] for x in dp[i] }, 0 <= i < len

Time complexity: O(2^n)
Space complexity: O(2^n)

C++

// Author: Huahua

bool isPalindrome(const string& s) {

const int n = s.length();

for (int i = 0; i < n / 2; ++i)

if (s[i] != s[n - 1 - i]) return false;

return true;

}

class Solution {

public:

vector<vector<string>> partition(string s) {

int n = s.length();

vector<vector<vector<string>>> dp(n + 1);

for (int len = 1; len <= n; ++len) {

for (int i = 0; i < len; ++i) {

string right = s.substr(i, len - i);

if (!isPalindrome(right)) continue;

if (i == 0) dp[len].push_back({right});

for (const auto& p : dp[i]) {

dp[len].push_back(p);

dp[len].back().push_back(right);

}

return dp[n];

}

};

Solution 2: DFS

Time complexity: O(2^n)
Space complexity: O(n)

C++

// Author: Huahua

bool isPalindrome(const string& s, int l, int r) {

while (l < r)

if (s[l++] != s[r--]) return false;

return true;

}

class Solution {

public:

vector<vector<string>> partition(string s) {

int n = s.length();

vector<vector<string>> ans;

vector<string> cur;

function<void(int)> dfs = [&](int start) {

if (start == n) {

ans.push_back(cur);

return;

}

for (int i = start; i < n; ++i) {

if (!isPalindrome(s, start, i)) continue;

cur.push_back(s.substr(start, i - start + 1));

dfs(i + 1);

cur.pop_back();

}

};

dfs(0);

return ans;

}

};

花花酱 LeetCode 130. Surrounded Regions

By zxi on October 9, 2019

Given a 2D board containing 'X' and 'O' (the letter O), capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

Example:

X X X X
X O O X
X X O X
X O X X

After running your function, the board should be:

X X X X
X X X X
X X X X
X O X X

Explanation:

Surrounded regions shouldn’t be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Solution: DFS

Time complexity: O(m*n)
Space complexity: O(m*n)

Only starts DFS at border cells of O.

C++

// Author: Huahua

class Solution {

public:

void solve(vector<vector<char>>& board) {

const int m = board.size();

if (m == 0) return;

const int n = board[0].size();

function<void(int, int)> dfs = [&](int x, int y) {

if (x < 0 || x >= n || y < 0 || y >= m || board[y][x] != 'O') return;

board[y][x] = 'G'; // mark it as good

dfs(x - 1, y);

dfs(x + 1, y);

dfs(x, y - 1);

dfs(x, y + 1);

};

for (int y = 0; y < m; ++y)

dfs(0, y), dfs(n - 1, y);

for (int x = 0; x < n; ++x)

dfs(x, 0), dfs(x, m - 1);

map<char, char> v{{'G','O'},{'O','X'}, {'X','X'}};

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

board[y][x] = v[board[y][x]];

}

};