Posts tagged as “fenwick tree”

花花酱 LeetCode 1649. Create Sorted Array through Instructions

By zxi on November 8, 2020

Given an integer array instructions, you are asked to create a sorted array from the elements in instructions. You start with an empty container nums. For each element from left to right in instructions, insert it into nums. The cost of each insertion is the minimum of the following:

The number of elements currently in nums that are strictly less than instructions[i].
The number of elements currently in nums that are strictly greater than instructions[i].

For example, if inserting element 3 into nums = [1,2,3,5], the cost of insertion is min(2, 1) (elements 1 and 2 are less than 3, element 5 is greater than 3) and nums will become [1,2,3,3,5].

Return the total cost to insert all elements from instructions into nums. Since the answer may be large, return it modulo 10⁹ + 7

Example 1:

Input: instructions = [1,5,6,2]
Output: 1
Explanation: Begin with nums = [].
Insert 1 with cost min(0, 0) = 0, now nums = [1].
Insert 5 with cost min(1, 0) = 0, now nums = [1,5].
Insert 6 with cost min(2, 0) = 0, now nums = [1,5,6].
Insert 2 with cost min(1, 2) = 1, now nums = [1,2,5,6].
The total cost is 0 + 0 + 0 + 1 = 1.

Example 2:

Input: instructions = [1,2,3,6,5,4]
Output: 3
Explanation: Begin with nums = [].
Insert 1 with cost min(0, 0) = 0, now nums = [1].
Insert 2 with cost min(1, 0) = 0, now nums = [1,2].
Insert 3 with cost min(2, 0) = 0, now nums = [1,2,3].
Insert 6 with cost min(3, 0) = 0, now nums = [1,2,3,6].
Insert 5 with cost min(3, 1) = 1, now nums = [1,2,3,5,6].
Insert 4 with cost min(3, 2) = 2, now nums = [1,2,3,4,5,6].
The total cost is 0 + 0 + 0 + 0 + 1 + 2 = 3.

Example 3:

Input: instructions = [1,3,3,3,2,4,2,1,2]
Output: 4
Explanation: Begin with nums = [].
Insert 1 with cost min(0, 0) = 0, now nums = [1].
Insert 3 with cost min(1, 0) = 0, now nums = [1,3].
Insert 3 with cost min(1, 0) = 0, now nums = [1,3,3].
Insert 3 with cost min(1, 0) = 0, now nums = [1,3,3,3].
Insert 2 with cost min(1, 3) = 1, now nums = [1,2,3,3,3].
Insert 4 with cost min(5, 0) = 0, now nums = [1,2,3,3,3,4].
Insert 2 with cost min(1, 4) = 1, now nums = [1,2,2,3,3,3,4].
Insert 1 with cost min(0, 6) = 0, now nums = [1,1,2,2,3,3,3,4].
Insert 2 with cost min(2, 4) = 2, now nums = [1,1,2,2,2,3,3,3,4].
The total cost is 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 + 2 = 4.

Constraints:

1 <= instructions.length <= 10⁵
1 <= instructions[i] <= 10⁵

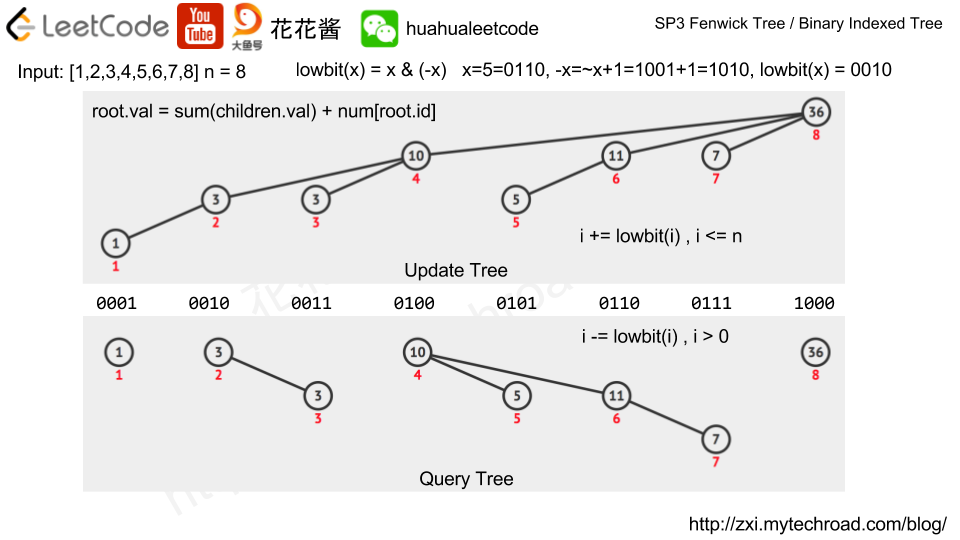
Solution: Fenwick Tree / Binary Indexed Tree

Time complexity: O(nlogm)
Space complexity: O(m + n)

m is the maximum value, n is number of values.

C++

class FenwickTree {

public:

FenwickTree(int n): sums_(n + 1, 0) {}

void update(int i, int delta) {

while (i < sums_.size()) {

sums_[i] += delta;

i += lowbit(i);

}

int query(int i) const {

int sum = 0;

while (i > 0) {

sum += sums_[i];

i -= lowbit(i);

}

return sum;

}

private:

static inline int lowbit(int x) {

return x & (-x);

}

vector<int> sums_;

};

class Solution {

public:

int createSortedArray(vector<int>& instructions) {

const int n = instructions.size();

FenwickTree tree(1e5);

long ans = 0;

for (int i = 0; i < n; ++i) {

int lt = tree.query(instructions[i] - 1);

int gt = i - tree.query(instructions[i]);

ans += min(lt, gt);

tree.update(instructions[i], 1);

}

return ans % 1000000007;

}

};

花花酱 LeetCode 1409. Queries on a Permutation With Key

By zxi on April 11, 2020

Given the array queries of positive integers between 1 and m, you have to process all queries[i] (from i=0 to i=queries.length-1) according to the following rules:

In the beginning, you have the permutation P=[1,2,3,...,m].
For the current i, find the position of queries[i] in the permutation P (indexing from 0) and then move this at the beginning of the permutation P. Notice that the position of queries[i] in P is the result for queries[i].

Return an array containing the result for the given queries.

Example 1:

Input: queries = [3,1,2,1], m = 5
Output: [2,1,2,1] 
Explanation: The queries are processed as follow: 
For i=0: queries[i]=3, P=[1,2,3,4,5], position of 3 in P is 2, then we move 3 to the beginning of P resulting in P=[3,1,2,4,5]. 
For i=1: queries[i]=1, P=[3,1,2,4,5], position of 1 in P is 1, then we move 1 to the beginning of P resulting in P=[1,3,2,4,5]. 
For i=2: queries[i]=2, P=[1,3,2,4,5], position of 2 in P is 2, then we move 2 to the beginning of P resulting in P=[2,1,3,4,5]. 
For i=3: queries[i]=1, P=[2,1,3,4,5], position of 1 in P is 1, then we move 1 to the beginning of P resulting in P=[1,2,3,4,5]. 
Therefore, the array containing the result is [2,1,2,1].

Example 2:

Input: queries = [4,1,2,2], m = 4
Output: [3,1,2,0]

Example 3:

Input: queries = [7,5,5,8,3], m = 8
Output: [6,5,0,7,5]

Constraints:

1 <= m <= 10^3
1 <= queries.length <= m
1 <= queries[i] <= m

Solution1: Simulation + Hashtable

Use a hashtable to store the location of each key.
For each query q, use h[q] to get the index of q, for each key, if its current index is less than q, increase their indices by 1. (move right). Set h[q] to 0.

Time complexity: O(q*m)
Space complexity: O(m)

C++

class Solution {

public:

vector<int> processQueries(vector<int>& queries, int m) {

vector<int> p(m + 1);

iota(begin(p), end(p), -1);

vector<int> ans;

for (int q : queries) {

ans.push_back(p[q]);

for (int i = 1; i <= m; ++i)

if (p[i] < p[q]) ++p[i];

p[q] = 0;

}

return ans;

}

};

Solution 2: Fenwick Tree + HashTable

Time complexity: O(qlogm)
Space complexity: O(m)

C++

// Author: Huahua

class Fenwick {

public:

explicit Fenwick(int n): vals_(n) {}

// sum(A[1~i])

int query(int i) const {

int s = 0;

while (i > 0) {

s += vals_[i];

i -= i & -i;

}

return s;

}

// A[i] += delta

void update(int i, int delta) {

while (i < vals_.size()) {

vals_[i] += delta;

i += i & -i;

}

private:

vector<int> vals_;

};

class Solution {

public:

vector<int> processQueries(vector<int>& queries, int m) {

Fenwick tree(m * 2 + 1);

vector<int> pos(m + 1);

for (int i = 1; i <= m; ++i)

tree.update(pos[i] = i + m, 1);

vector<int> ans;

for (int q : queries) {

ans.push_back(tree.query(pos[q] - 1));

tree.update(pos[q], -1); // set to 0.

tree.update(pos[q] = m--, 1); // move to the front.

}

return ans;

}

};

Python3

class Fenwick:

def __init__(self, n):

self.n = n

self.val = [0] * n

def query(self, i):

s = 0

while i > 0:

s += self.val[i]

i -= i & -i

return s

def update(self, i, delta):

while i < self.n:

self.val[i] += delta

i += i & -i

class Solution:

def processQueries(self, queries: List[int], m: int) -> List[int]:

pos = [i + m for i in range(m + 1)]

tree = Fenwick(2 * m + 1)

for i in range(1, m + 1): tree.update(i + m, 1)

ans = []

for q in queries:

ans.append(tree.query(pos[q] - 1))

tree.update(pos[q], -1)

pos[q] = m

m -= 1

tree.update(pos[q], 1)

return ans

花花酱 Fenwick Tree / Binary Indexed Tree / 树状数组 SP3

By zxi on January 3, 2018

本期节目中我们介绍了Fenwick Tree/Binary Indexed Tree/树状数组的原理和实现以及它在leetcode中的应用。
In this episode, we will introduce Fenwick Tree/Binary Indexed Tree, its idea and implementation and show its applications in leetcode.

Fenwick Tree is mainly designed for solving the single point update range sum problems. e.g. what’s the sum between i-th and j-th element while the values of the elements are mutable.

Init the tree (include building all prefix sums) takes O(nlogn)

Update the value of an element takes O(logn)

Query the range sum takes O(logn)

Space complexity: O(n)

Applications:

Implementation:

C++

class FenwickTree {

public:

FenwickTree(int n): sums_(n + 1, 0) {}

void update(int i, int delta) {

while (i < sums_.size()) {

sums_[i] += delta;

i += lowbit(i);

}

int query(int i) const {

int sum = 0;

while (i > 0) {

sum += sums_[i];

i -= lowbit(i);

}

return sum;

}

private:

static inline int lowbit(int x) {

return x & (-x);

}

vector<int> sums_;

};

Java

class FenwickTree {

int sums_[];

public FenwickTree(int n) {

sums_ = new int[n + 1];

}

public void update(int i, int delta) {

while (i < sums_.length) {

sums_[i] += delta;

i += i & -i;

}

public int query(int i) {

int sum = 0;

while (i > 0) {

sum += sums_[i];

i -= i & -i;

}

return sum;

}

Python3

class FenwickTree:

def __init__(self, n):

self._sums = [0 for _ in range(n + 1)]

def update(self, i, delta):

while i < len(self._sums):

self._sums[i] += delta

i += i & -i

def query(self, i):

s = 0

while i > 0:

s += self._sums[i]

i -= i & -i

return s

Applications

花花酱 LeetCode 315. Count of Smaller Numbers After Self

By zxi on January 3, 2018

题目大意：给你一个数组，对于数组中的每个元素，返回一共有多少在它之后的元素比它小。

Problem:

You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].

Example:

Given nums = [5, 2, 6, 1]

To the right of 5 there are 2 smaller elements (2 and 1).

To the right of 2 there is only 1 smaller element (1).

To the right of 6 there is 1 smaller element (1).

To the right of 1 there is 0 smaller element.

Return the array [2, 1, 1, 0].

Idea:

Fenwick Tree / Binary Indexed Tree

BST

Solution 1: Binary Indexed Tree (Fenwick Tree)

C++

// Author: Huahua

// Runnning time: 32 ms

// Time complexity: O(nlogn)

// Space complexity: O(k), k is the number unique elements

class FenwickTree {

public:

FenwickTree(int n): sums_(n + 1, 0) {}

void update(int i, int delta) {

while (i < sums_.size()) {

sums_[i] += delta;

i += lowbit(i);

}

int query(int i) const {

int sum = 0;

while (i > 0) {

sum += sums_[i];

i -= lowbit(i);

}

return sum;

}

private:

static inline int lowbit(int x) { return x & (-x); }

vector<int> sums_;

};

class Solution {

public:

vector<int> countSmaller(vector<int>& nums) {

// Sort the unique numbers

set<int> sorted(nums.begin(), nums.end());

// Map the number to its rank

unordered_map<int, int> ranks;

int rank = 0;

for (const int num : sorted)

ranks[num] = ++rank;

vector<int> ans;

FenwickTree tree(ranks.size());

// Scan the numbers in reversed order

for (int i = nums.size() - 1; i >= 0; --i) {

// Chechk how many numbers are smaller than the current number.

ans.push_back(tree.query(ranks[nums[i]] - 1));

// Increse the count of the rank of current number.

tree.update(ranks[nums[i]], 1);

}

std::reverse(ans.begin(), ans.end());

return ans;

}

};

Java

// Author: Huahua

// Running time: 28 ms

class Solution {

private static int lowbit(int x) { return x & (-x); }

class FenwickTree {

private int[] sums;

public FenwickTree(int n) {

sums = new int[n + 1];

}

public void update(int i, int delta) {

while (i < sums.length) {

sums[i] += delta;

i += lowbit(i);

}

public int query(int i) {

int sum = 0;

while (i > 0) {

sum += sums[i];

i -= lowbit(i);

}

return sum;

}

};

public List<Integer> countSmaller(int[] nums) {

int[] sorted = Arrays.copyOf(nums, nums.length);

Arrays.sort(sorted);

Map<Integer, Integer> ranks = new HashMap<>();

int rank = 0;

for (int i = 0; i < sorted.length; ++i)

if (i == 0 || sorted[i] != sorted[i - 1])

ranks.put(sorted[i], ++rank);

FenwickTree tree = new FenwickTree(ranks.size());

List<Integer> ans = new ArrayList<Integer>();

for (int i = nums.length - 1; i >= 0; --i) {

int sum = tree.query(ranks.get(nums[i]) - 1);

ans.add(tree.query(ranks.get(nums[i]) - 1));

tree.update(ranks.get(nums[i]), 1);

}

Collections.reverse(ans);

return ans;

}

Solution 2: BST

C++

// Author: Huahua

// Running time: 26 ms

struct BSTNode {

int val;

int count;

int left_count;

BSTNode* left;

BSTNode* right;

BSTNode(int val): val(val), count(1), left_count(0), left{nullptr}, right{nullptr} {}

~BSTNode() { delete left; delete right; }

int less_or_equal() const { return count + left_count; }

};

class Solution {

public:

vector<int> countSmaller(vector<int>& nums) {

if (nums.empty()) return {};

std::reverse(nums.begin(), nums.end());

std::unique_ptr<BSTNode> root(new BSTNode(nums[0]));

vector<int> ans{0};

for (int i = 1; i < nums.size(); ++i)

ans.push_back(insert(root.get(), nums[i]));

std::reverse(ans.begin(), ans.end());

return ans;

}

private:

// Returns the number of elements smaller than val under root.

int insert(BSTNode* root, int val) {

if (root->val == val) {

++root->count;

return root->left_count;

} else if (val < root->val) {

++root->left_count;

if (root->left == nullptr) {

root->left = new BSTNode(val);

return 0;

}

return insert(root->left, val);

} else {

if (root->right == nullptr) {

root->right = new BSTNode(val);

return root->less_or_equal();

}

return root->less_or_equal() + insert(root->right, val);

}

};

Java

// Author: Huahua

// Running time: 10 ms

class Solution {

class Node {

int val;

int count;

int left_count;

Node left;

Node right;

public Node(int val) { this.val = val; this.count = 1; }

public int less_or_equal() { return count + left_count; }

}

public List<Integer> countSmaller(int[] nums) {

List<Integer> ans = new ArrayList<>();

if (nums.length == 0) return ans;

int n = nums.length;

Node root = new Node(nums[n - 1]);

ans.add(0);

for (int i = n - 2; i >= 0; --i)

ans.add(insert(root, nums[i]));

Collections.reverse(ans);

return ans;

}

private int insert(Node root, int val) {

if (root.val == val) {

++root.count;

return root.left_count;

} else if (val < root.val) {

++root.left_count;

if (root.left == null) {

root.left = new Node(val);

return 0;

}

return insert(root.left, val);

} else {

if (root.right == null) {

root.right = new Node(val);

return root.less_or_equal();

}

return root.less_or_equal() + insert(root.right, val);

}

花花酱 307. Range Sum Query – Mutable

By zxi on January 3, 2018

题目大意：给你一个数组，让你求一个范围之内所有元素的和，数组元素可以更改。

Problem:

Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.

The update(i, val) function modifies nums by updating the element at index i to val.

Example:

Given nums = [1, 3, 5]

sumRange(0, 2) -> 9

update(1, 2)

sumRange(0, 2) -> 8

Note:

The array is only modifiable by the update function.
You may assume the number of calls to update and sumRange function is distributed evenly.

Idea:

Fenwick Tree

Solution:

C++

Time complexity:

init O(nlogn)

query: O(logn)

update: O(logn)

C++

// Author: Huahua

// Running time: 83 ms

class FenwickTree {

public:

FenwickTree(int n): sums_(n + 1, 0) {}

void update(int i, int delta) {

while (i < sums_.size()) {

sums_[i] += delta;

i += lowbit(i);

}

int query(int i) const {

int sum = 0;

while (i > 0) {

sum += sums_[i];

i -= lowbit(i);

}

return sum;

}

private:

static inline int lowbit(int x) { return x & (-x); }

vector<int> sums_;

};

class NumArray {

public:

NumArray(vector<int> nums): nums_(std::move(nums)), tree_(nums_.size()) {

for (int i = 0; i < nums_.size(); ++i)

tree_.update(i + 1, nums_[i]);

}

void update(int i, int val) {

tree_.update(i + 1, val - nums_[i]);

nums_[i] = val;

}

int sumRange(int i, int j) {

return tree_.query(j + 1) - tree_.query(i);

}

private:

vector<int> nums_;

FenwickTree tree_;

};

Java

// Author: Huahua

// Running time: 130 ms

class NumArray {

FenwickTree tree_;

int[] nums_;

public NumArray(int[] nums) {

nums_ = nums;

tree_ = new FenwickTree(nums.length);

for (int i = 0; i < nums.length; ++i)

tree_.update(i + 1, nums[i]);

}

public void update(int i, int val) {

tree_.update(i + 1, val - nums_[i]);

nums_[i] = val;

}

public int sumRange(int i, int j) {

return tree_.query(j + 1) - tree_.query(i);

}

class FenwickTree {

int sums_[];

public FenwickTree(int n) {

sums_ = new int[n + 1];

}

public void update(int i, int delta) {

while (i < sums_.length) {

sums_[i] += delta;

i += i & -i;

}

public int query(int i) {

int sum = 0;

while (i > 0) {

sum += sums_[i];

i -= i & -i;

}

return sum;

}

Python3

"""

Author: Huahua

Running time: 192 ms (< 90.00%)

"""

class FenwickTree:

def __init__(self, n):

self._sums = [0 for _ in range(n + 1)]

def update(self, i, delta):

while i < len(self._sums):

self._sums[i] += delta

i += i & -i

def query(self, i):

s = 0

while i > 0:

s += self._sums[i]

i -= i & -i

return s

class NumArray:

def __init__(self, nums):

self._nums = nums

self._tree = FenwickTree(len(nums))

for i in range(len(nums)):

self._tree.update(i + 1, nums[i])

def update(self, i, val):

self._tree.update(i + 1, val - self._nums[i])

self._nums[i] = val

def sumRange(self, i, j):

return self._tree.query(j + 1) - self._tree.query(i)

Solution 2: Segment Tree

C++

// Author: Huahua, running time: 24 ms

class SegmentTreeNode {

public:

SegmentTreeNode(int start, int end, int sum,

SegmentTreeNode* left = nullptr,

SegmentTreeNode* right = nullptr):

start(start),

end(end),

sum(sum),

left(left),

right(right){}

SegmentTreeNode(const SegmentTreeNode&) = delete;

SegmentTreeNode& operator=(const SegmentTreeNode&) = delete;

~SegmentTreeNode() {

delete left;

delete right;

left = right = nullptr;

}

int start;

int end;

int sum;

SegmentTreeNode* left;

SegmentTreeNode* right;

};

class NumArray {

public:

NumArray(vector<int> nums) {

nums_.swap(nums);

if (!nums_.empty())

root_.reset(buildTree(0, nums_.size() - 1));

}

void update(int i, int val) {

updateTree(root_.get(), i, val);

}

int sumRange(int i, int j) {

return sumRange(root_.get(), i, j);

}

private:

vector<int> nums_;

std::unique_ptr<SegmentTreeNode> root_;

SegmentTreeNode* buildTree(int start, int end) {

if (start == end) {

return new SegmentTreeNode(start, end, nums_[start]);

}

int mid = start + (end - start) / 2;

auto left = buildTree(start, mid);

auto right = buildTree(mid + 1, end);

auto node = new SegmentTreeNode(start, end, left->sum + right->sum, left, right);

return node;

}

void updateTree(SegmentTreeNode* root, int i, int val) {

if (root->start == i && root->end == i) {

root->sum = val;

return;

}

int mid = root->start + (root->end - root->start) / 2;

if (i <= mid) {

updateTree(root->left, i, val);

} else {

updateTree(root->right, i, val);

}

root->sum = root->left->sum + root->right->sum;

}

int sumRange(SegmentTreeNode* root, int i, int j) {

if (i == root->start && j == root->end) {

return root->sum;

}

int mid = root->start + (root->end - root->start) / 2;

if (j <= mid) {

return sumRange(root->left, i, j);

} else if (i > mid) {

return sumRange(root->right, i, j);

} else {

return sumRange(root->left, i, mid) + sumRange(root->right, mid + 1, j);

}

};