Posts tagged as “game”

花花酱 LeetCode 1872. Stone Game VIII

By zxi on August 5, 2021

Alice and Bob take turns playing a game, with Alice starting first.

There are n stones arranged in a row. On each player’s turn, while the number of stones is more than one, they will do the following:

Choose an integer x > 1, and remove the leftmost x stones from the row.
Add the sum of the removed stones’ values to the player’s score.
Place a new stone, whose value is equal to that sum, on the left side of the row.

The game stops when only one stone is left in the row.

The score difference between Alice and Bob is (Alice's score - Bob's score). Alice’s goal is to maximize the score difference, and Bob’s goal is the minimize the score difference.

Given an integer array stones of length n where stones[i] represents the value of the i^th stone from the left, return the score difference between Alice and Bob if they both play optimally.

Example 1:

Input: stones = [-1,2,-3,4,-5]
Output: 5
Explanation:
- Alice removes the first 4 stones, adds (-1) + 2 + (-3) + 4 = 2 to her score, and places a stone of
  value 2 on the left. stones = [2,-5].
- Bob removes the first 2 stones, adds 2 + (-5) = -3 to his score, and places a stone of value -3 on
  the left. stones = [-3].
The difference between their scores is 2 - (-3) = 5.

Example 2:

Input: stones = [7,-6,5,10,5,-2,-6]
Output: 13
Explanation:
- Alice removes all stones, adds 7 + (-6) + 5 + 10 + 5 + (-2) + (-6) = 13 to her score, and places a
  stone of value 13 on the left. stones = [13].
The difference between their scores is 13 - 0 = 13.

Example 3:

Input: stones = [-10,-12]
Output: -22
Explanation:
- Alice can only make one move, which is to remove both stones. She adds (-10) + (-12) = -22 to her
  score and places a stone of value -22 on the left. stones = [-22].
The difference between their scores is (-22) - 0 = -22.

Constraints:

n == stones.length
2 <= n <= 10⁵
-10⁴ <= stones[i] <= 10⁴

Solution: Prefix Sum + DP

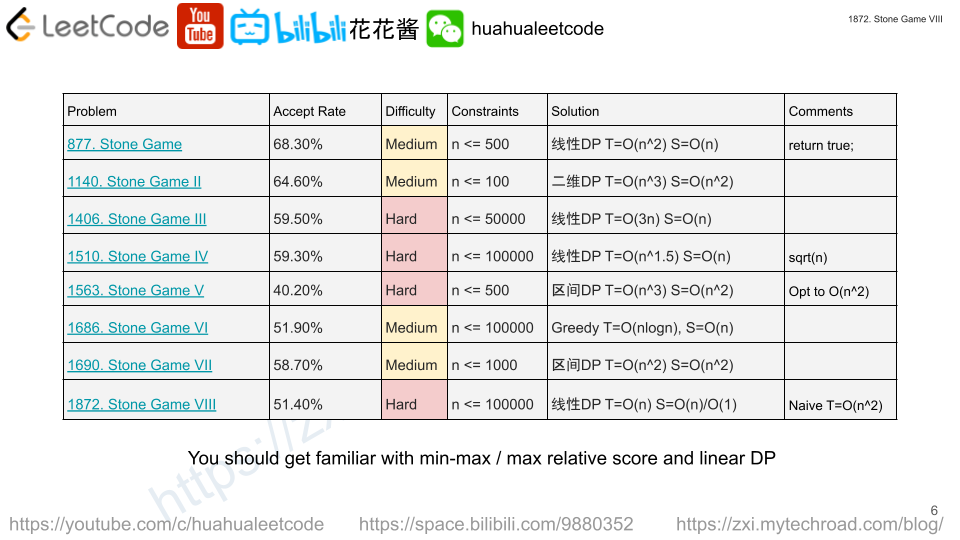
Note: Naive DP (min-max) takes O(n²) which leads to TLE. The key of this problem is that each player takes k stones, but put their sum back as a new stone, so you can assume all the original stones are still there, but opponent has to start from the k+1 th stone.

Let dp[i] denote the max score diff that current player can achieve by taking stones[0~i] (or equivalent)

dp[n-1] = sum(A[0~n-1]) // Alice takes all the stones.
dp[n-2] = sum(A[0~n-2]) – (A[n-1] + sum(A[0~n-2])) = sum(A[0~n-2]) – dp[n-1] // Alice takes n-1 stones, Bob take the last one (A[n-1]) + put-back-stone.
dp[n-3] = sum(A[0~n-3]) – max(dp[n-2], dp[n-1]) // Alice takes n-2 stones, Bob has two options (takes n-1 stones or takes n stones)
…
dp[0] = A[0] – max(dp[n-1], dp[n-1], …, dp[1]) // Alice takes the first stone, Bob has n-1 options.

Time complexity: O(n)
Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int stoneGameVIII(vector<int>& stones) {

const int n = stones.size();

for (int i = 1; i < n; ++i)

stones[i] += stones[i - 1];

int ans = stones.back(); // take all the stones.

for (int i = n - 2; i > 0; --i)

ans = max(ans, stones[i] - ans);

return ans;

}

};

花花酱 LeetCode 1690. Stone Game VII

By zxi on December 13, 2020

Alice and Bob take turns playing a game, with Alice starting first.

There are n stones arranged in a row. On each player’s turn, they can remove either the leftmost stone or the rightmost stone from the row and receive points equal to the sum of the remaining stones’ values in the row. The winner is the one with the higher score when there are no stones left to remove.

Bob found that he will always lose this game (poor Bob, he always loses), so he decided to minimize the score’s difference. Alice’s goal is to maximize the difference in the score.

Given an array of integers stones where stones[i] represents the value of the i^th stone from the left, return the difference in Alice and Bob’s score if they both play optimally.

Example 1:

Input: stones = [5,3,1,4,2]
Output: 6
Explanation: 
- Alice removes 2 and gets 5 + 3 + 1 + 4 = 13 points. Alice = 13, Bob = 0, stones = [5,3,1,4].
- Bob removes 5 and gets 3 + 1 + 4 = 8 points. Alice = 13, Bob = 8, stones = [3,1,4].
- Alice removes 3 and gets 1 + 4 = 5 points. Alice = 18, Bob = 8, stones = [1,4].
- Bob removes 1 and gets 4 points. Alice = 18, Bob = 12, stones = [4].
- Alice removes 4 and gets 0 points. Alice = 18, Bob = 12, stones = [].
The score difference is 18 - 12 = 6.

Example 2:

Input: stones = [7,90,5,1,100,10,10,2]
Output: 122

Constraints:

n == stones.length
2 <= n <= 1000
1 <= stones[i] <= 1000

Solution: MinMax + DP

For a sub game of stones[l~r] game(l, r), we have two choices:
Remove the left one: sum(stones[l + 1 ~ r]) – game(l + 1, r)
Remove the right one: sum(stones[l ~ r – 1]) – game(l, r – 1)
And take the best choice.

Time complexity: O(n^2)
Space complexity: O(n^2)

C++/Top Down

// Author: Huahua

class Solution {

public:

int stoneGameVII(vector<int>& A) {

const int n = A.size();

vector<vector<int>> cache(n, vector<int>(n, INT_MAX));

function<int(int, int, int)> dp = [&](int l, int r, int s) {

if (l >= r) return 0;

if (cache[l][r] == INT_MAX)

cache[l][r] = max(s - A[r] - dp(l, r - 1, s - A[r]),

s - A[l] - dp(l + 1, r, s - A[l]));

return cache[l][r];

};

return dp(0, n - 1, accumulate(begin(A), end(A), 0));

}

};

C++/Bottom-Up

// Author: Huahua

class Solution {

public:

int stoneGameVII(vector<int>& A) {

const int n = A.size();

vector<int> s(n + 1);

for (int i = 0; i < n; ++i) s[i + 1] = s[i] + A[i];

vector<vector<int>> dp(n, vector<int>(n, 0));

for (int c = 2; c <= n; ++c)

for (int l = 0, r = l + c - 1; r < n; ++l, ++r)

dp[l][r] = max(s[r + 1] - s[l + 1] - dp[l + 1][r],

s[r] - s[l] - dp[l][r - 1]);

return dp[0][n - 1];

}

};

Python3

# Author: Huahua

class Solution:

def stoneGameVII(self, stones: List[int]) -> int:

n = len(stones)

s = [0] * (n + 1)

for i in range(n): s[i + 1] = s[i] + stones[i]

dp = [[0] * n for _ in range(n)]

for c in range(2, n + 1):

for l in range(0, n - c + 1):

r = l + c - 1

dp[l][r] = max(s[r + 1] - s[l + 1] - dp[l + 1][r],

s[r] - s[l] - dp[l][r - 1])

return dp[0][n - 1]

花花酱 LeetCode 1686. Stone Game VI

By zxi on December 12, 2020

Alice and Bob take turns playing a game, with Alice starting first.

There are n stones in a pile. On each player’s turn, they can remove a stone from the pile and receive points based on the stone’s value. Alice and Bob may value the stones differently.

You are given two integer arrays of length n, aliceValues and bobValues. Each aliceValues[i] and bobValues[i] represents how Alice and Bob, respectively, value the i^th stone.

The winner is the person with the most points after all the stones are chosen. If both players have the same amount of points, the game results in a draw. Both players will play optimally.

Determine the result of the game, and:

If Alice wins, return 1.
If Bob wins, return -1.
If the game results in a draw, return 0.

Example 1:

Input: aliceValues = [1,3], bobValues = [2,1]
Output: 1
Explanation:
If Alice takes stone 1 (0-indexed) first, Alice will receive 3 points.
Bob can only choose stone 0, and will only receive 2 points.
Alice wins.

Example 2:

Input: aliceValues = [1,2], bobValues = [3,1]
Output: 0
Explanation:
If Alice takes stone 0, and Bob takes stone 1, they will both have 1 point.
Draw.

Example 3:

Input: aliceValues = [2,4,3], bobValues = [1,6,7]
Output: -1
Explanation:
Regardless of how Alice plays, Bob will be able to have more points than Alice.
For example, if Alice takes stone 1, Bob can take stone 2, and Alice takes stone 0, Alice will have 6 points to Bob's 7.
Bob wins.

Constraints:

n == aliceValues.length == bobValues.length
1 <= n <= 10⁵
1 <= aliceValues[i], bobValues[i] <= 100

Solution: Greedy

Sort by the sum of stone values.

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int stoneGameVI(vector<int>& A, vector<int>& B) {

const int n = A.size();

vector<pair<int, int>> s(n);

for (int i = 0; i < n; ++i)

s.emplace_back(A[i] + B[i], i);

sort(rbegin(s), rend(s));

int ans = 0;

for (int i = 0; i < n; ++i) {

int idx = s[i].second;

ans += (i & 1 ? B[idx] : A[idx]) * (i & 1 ? -1 : 1);

}

return ans < 0 ? -1 : (ans > 0);

}

};

花花酱 LeetCode 1510. Stone Game IV

By zxi on July 17, 2020

Alice and Bob take turns playing a game, with Alice starting first.

Initially, there are n stones in a pile. On each player’s turn, that player makes a move consisting of removing any non-zero square number of stones in the pile.

Also, if a player cannot make a move, he/she loses the game.

Given a positive integer n. Return True if and only if Alice wins the game otherwise return False, assuming both players play optimally.

Example 1:

Input: n = 1
Output: true
Explanation: Alice can remove 1 stone winning the game because Bob doesn't have any moves.

Example 2:

Input: n = 2
Output: false
Explanation: Alice can only remove 1 stone, after that Bob removes the last one winning the game (2 -> 1 -> 0).

Example 3:

Input: n = 4
Output: true
Explanation: n is already a perfect square, Alice can win with one move, removing 4 stones (4 -> 0).

Example 4:

Input: n = 7
Output: false
Explanation: Alice can't win the game if Bob plays optimally.
If Alice starts removing 4 stones, Bob will remove 1 stone then Alice should remove only 1 stone and finally Bob removes the last one (7 -> 3 -> 2 -> 1 -> 0). 
If Alice starts removing 1 stone, Bob will remove 4 stones then Alice only can remove 1 stone and finally Bob removes the last one (7 -> 6 -> 2 -> 1 -> 0).

Example 5:

Input: n = 17
Output: false
Explanation: Alice can't win the game if Bob plays optimally.

Constraints:

1 <= n <= 10^5

Solution: Recursion w/ Memoization / DP

Let win(n) denotes whether the current play will win or not.
Try all possible square numbers and see whether the other player will lose or not.
win(n) = any(win(n – i*i) == False) ? True : False
base case: win(0) = False

Time complexity: O(nsqrt(n))
Space complexity: O(n)

C++

class Solution {

public:

bool winnerSquareGame(int n) {

vector<int> cache(n + 1, 0); // 0:Unknown, 1:Win, -1:Lose

function<int(int)> win = [&](int n) -> int {

if (n == 0) return -1;

if (cache[n]) return cache[n];

for (int i = sqrt(n); i >= 1; --i)

if (win(n - i * i) < 0) return cache[n] = 1;

return cache[n] = -1;

};

return win(n) > 0;

}

};

Java

class Solution {

private int[] cache;

public boolean winnerSquareGame(int n) {

this.cache = new int[n + 1];

return this.win(n) > 0;

}

private int win(int n) {

if (n == 0) return -1;

if (this.cache[n] != 0) return this.cache[n];

for (int i = (int)Math.sqrt(n); i >= 1; --i)

if (win(n - i * i) < 0)

return this.cache[n] = 1;

return this.cache[n] = -1;

}

Python3

class Solution:

def winnerSquareGame(self, n: int) -> bool:

dp = [None] * (n + 1)

dp[0] = False

for i in range(0, n):

if dp[i]: continue

for j in range(1, n + 1):

if i + j * j > n: break

dp[i + j * j] = True

return dp[n]

花花酱 LeetCode 1406. Stone Game III

By zxi on April 5, 2020

Alice and Bob continue their games with piles of stones. There are several stones arranged in a row, and each stone has an associated value which is an integer given in the array stoneValue.

Alice and Bob take turns, with Alice starting first. On each player’s turn, that player can take 1, 2 or 3 stones from the first remaining stones in the row.

The score of each player is the sum of values of the stones taken. The score of each player is 0 initially.

The objective of the game is to end with the highest score, and the winner is the player with the highest score and there could be a tie. The game continues until all the stones have been taken.

Assume Alice and Bob play optimally.

Return “Alice” if Alice will win, “Bob” if Bob will win or “Tie” if they end the game with the same score.

Example 1:

Input: values = [1,2,3,7]
Output: "Bob"
Explanation: Alice will always lose. Her best move will be to take three piles and the score become 6. Now the score of Bob is 7 and Bob wins.

Example 2:

Input: values = [1,2,3,-9]
Output: "Alice"
Explanation: Alice must choose all the three piles at the first move to win and leave Bob with negative score.
If Alice chooses one pile her score will be 1 and the next move Bob's score becomes 5. The next move Alice will take the pile with value = -9 and lose.
If Alice chooses two piles her score will be 3 and the next move Bob's score becomes 3. The next move Alice will take the pile with value = -9 and also lose.
Remember that both play optimally so here Alice will choose the scenario that makes her win.

Example 3:

Input: values = [1,2,3,6]
Output: "Tie"
Explanation: Alice cannot win this game. She can end the game in a draw if she decided to choose all the first three piles, otherwise she will lose.

Example 4:

Input: values = [1,2,3,-1,-2,-3,7]
Output: "Alice"

Example 5:

Input: values = [-1,-2,-3]
Output: "Tie"

Constraints:

1 <= values.length <= 50000
-1000 <= values[i] <= 1000

Solution: DP with memorization

dp(i) := max relative score the current player can get if start the game from the i-th stone.

dp(i) = max(sum(values[i:i+k]) – dp(i + k)) 1 <= k <= 3

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

string stoneGameIII(vector<int>& stoneValue) {

const int n = stoneValue.size();

vector<int> mem(n, INT_MIN);

// Maximum `relative score` the current player can achieve

// if start from the i-th stone.

function<int(int)> dp = [&](int i) {

if (i >= n) return 0; // end of game.

if (mem[i] != INT_MIN) return mem[i];

for (int j = 0, s = 0; j < 3 && i + j < n; ++j) {

s += stoneValue[i + j];

// s - dp(.) to get `relative score`.

mem[i] = max(mem[i], s - dp(i + j + 1));

}

return mem[i];

};

const int score = dp(0);

return score > 0 ? "Alice" : (score == 0 ? "Tie" : "Bob");

}

};

Python3

# Author: Huahua

class Solution:

def stoneGameIII(self, stoneValue: List[int]) -> str:

n = len(stoneValue)

stoneValue += [0, 0, 0]

dp = [-10**9] * n + [0, 0, 0]

for i in range(n - 1, -1, -1):

for k in (1, 2, 3):

dp[i] = max(dp[i], sum(stoneValue[i:i+k]) - dp[i+k])

return "Alice" if dp[0] > 0 else "Bob" if dp[0] < 0 else "Tie"

Posts tagged as “game”

花花酱 LeetCode 1872. Stone Game VIII

Solution: Prefix Sum + DP

C++

花花酱 LeetCode 1690. Stone Game VII

Solution: MinMax + DP

C++/Top Down

C++/Bottom-Up

Python3

Related Problems

花花酱 LeetCode 1686. Stone Game VI

Solution: Greedy

C++

花花酱 LeetCode 1510. Stone Game IV

Solution: Recursion w/ Memoization / DP

C++

Java

Python3

花花酱 LeetCode 1406. Stone Game III

Solution: DP with memorization

C++

Python3

Related Problems