Posts tagged as “graph”

花花酱 LeetCode 743. Network Delay Time

By zxi on December 12, 2017

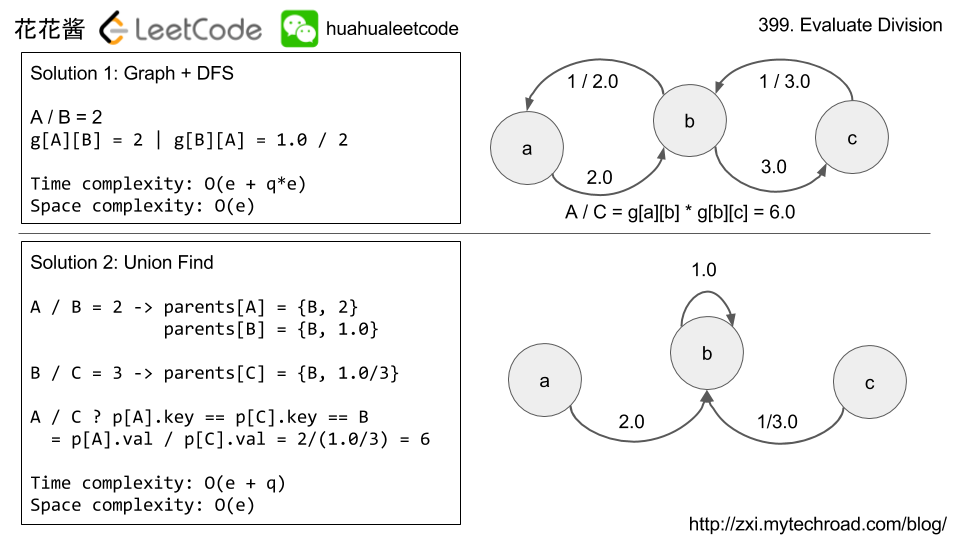
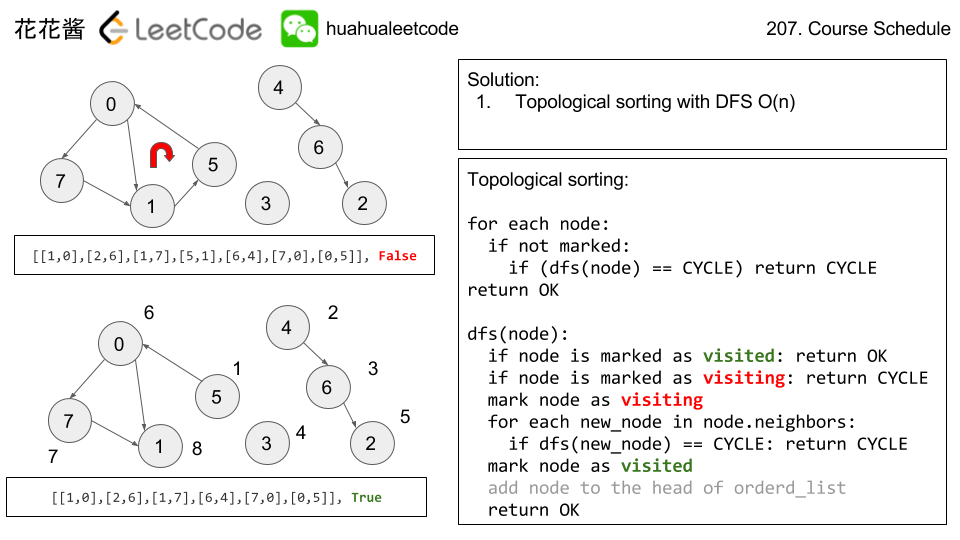
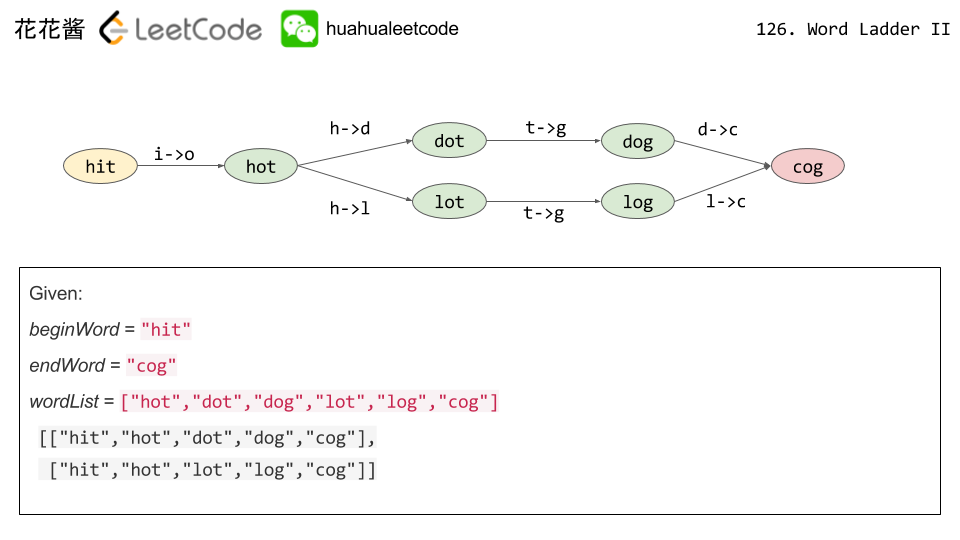
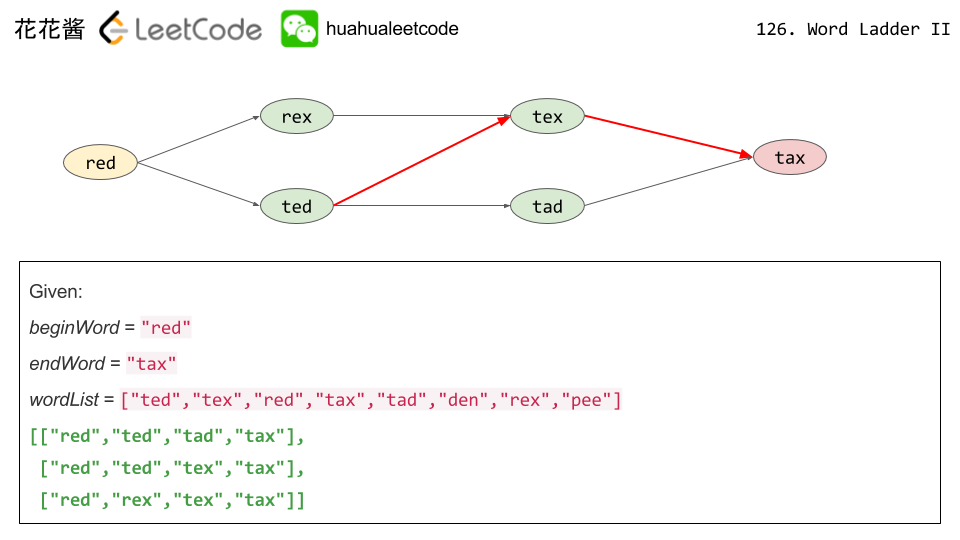
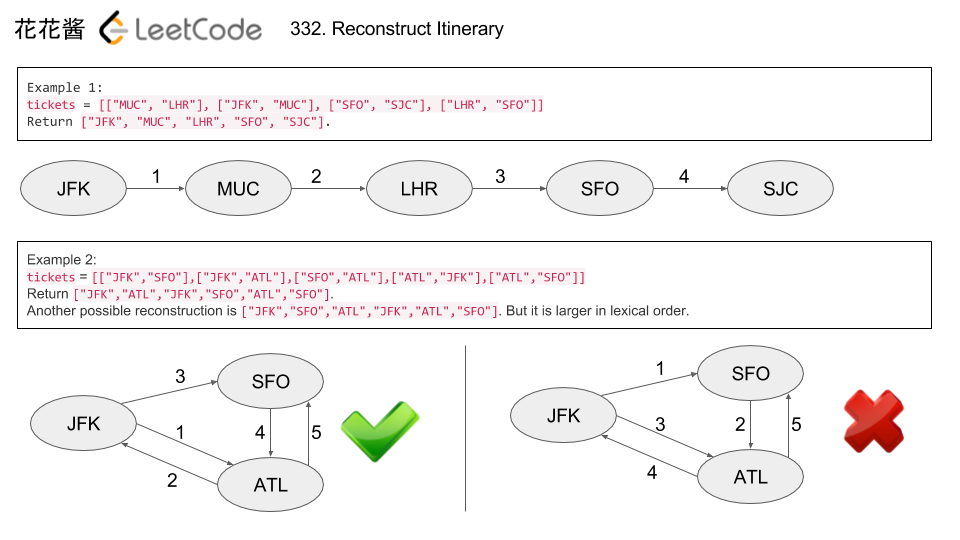
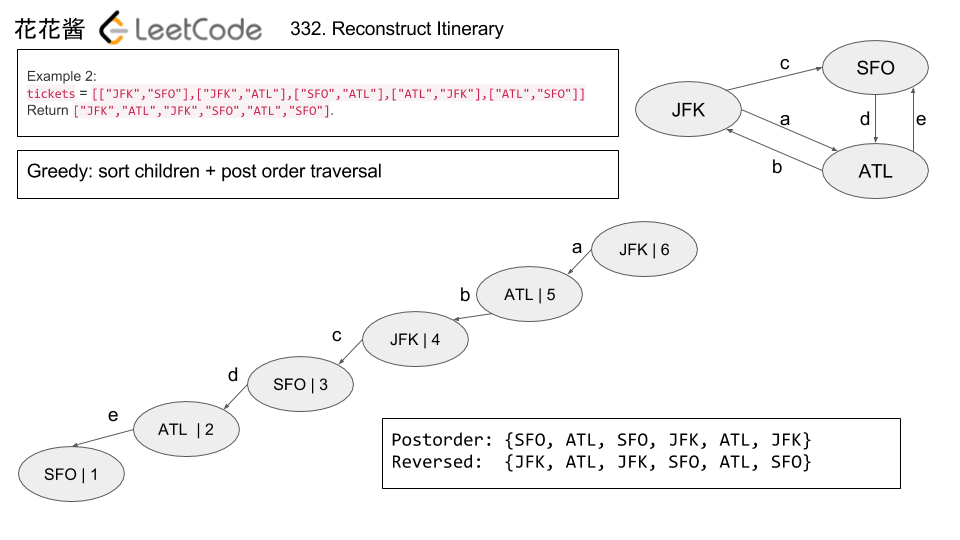
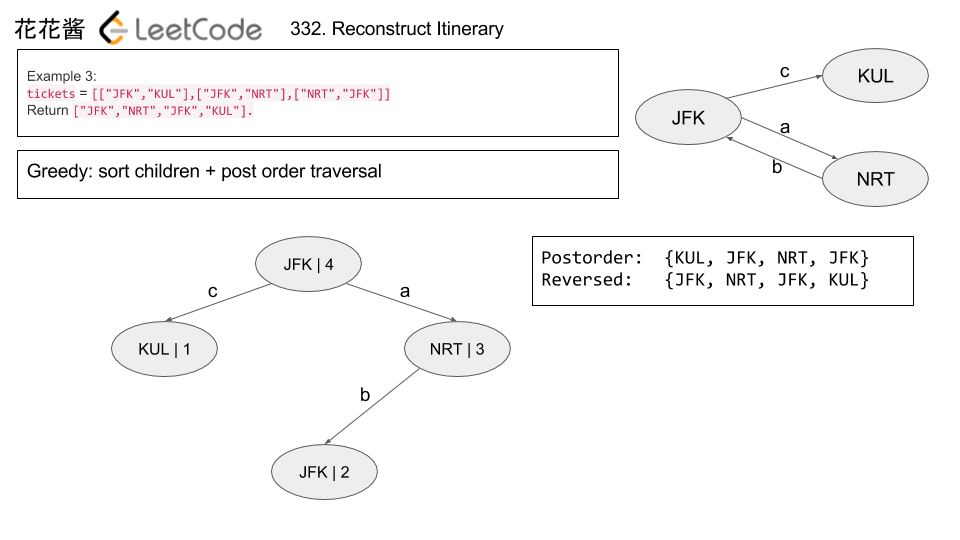
There are N network nodes, labelled 1 to N.

Given times, a list of travel times as directed edges times[i] = (u, v, w), where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.

Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal? If it is impossible, return -1.

Note:

N will be in the range [1, 100].
K will be in the range [1, N].
The length of times will be in the range [1, 6000].
All edges times[i] = (u, v, w) will have 1 <= u, v <= N and 1 <= w <= 100.

Idea:

Construct the graph and do a shortest path from K to all other nodes.

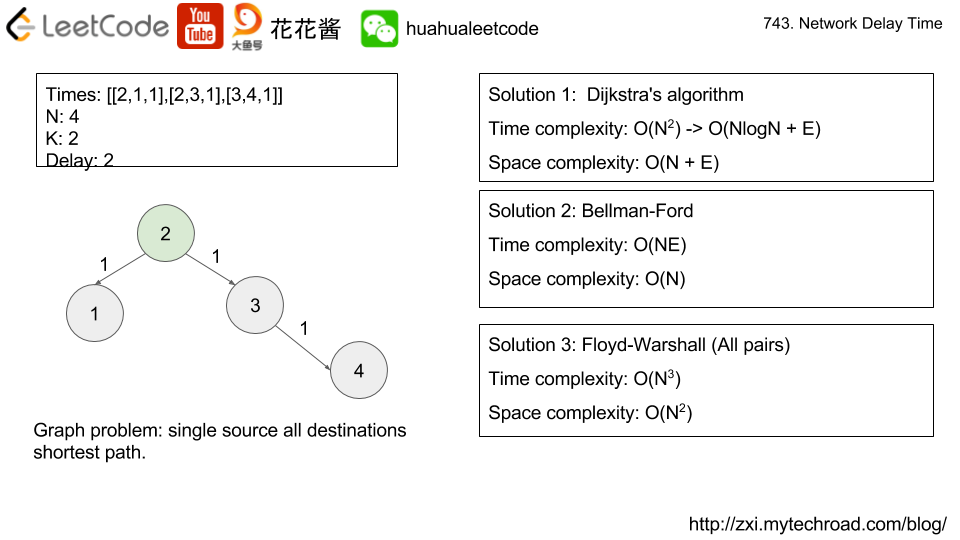
Solution 2:

C++ / Bellman-Ford

Time complexity: O(ne)

Space complexity: O(n)

// Author: Huahua

// Runtime: 92 ms

class Solution {

public:

int networkDelayTime(vector<vector<int>>& times, int N, int K) {

constexpr int MAX_TIME = 101 * 100;

vector<int> dist(N, MAX_TIME);

dist[K - 1] = 0;

for (int i = 1; i < N; ++i)

for (const auto& time : times) {

int u = time[0] - 1, v = time[1] - 1, w = time[2];

dist[v] = min(dist[v], dist[u] + w);

}

int max_dist = *max_element(dist.begin(), dist.end());

return max_dist == MAX_TIME ? -1 : max_dist;

}

};

Solution3:

C++ / Floyd-Warshall

Time complexity: O(n^3)

Space complexity: O(n^2)

// Author: Huahua

// Runtime: 92 ms

class Solution {

public:

int networkDelayTime(vector<vector<int>>& times, int N, int K) {

vector<vector<int>> d(N, vector<int>(N, -1));

for (auto time : times)

d[time[0] - 1][time[1] - 1] = time[2];

for (int i = 0; i < N; ++i)

d[i][i] = 0;

for (int k = 0; k < N; ++k)

for (int i = 0; i < N; ++i)

for (int j = 0; j < N; ++j)

if (d[i][k] >= 0 && d[k][j] >= 0)

if (d[i][j] < 0 || d[i][j] > d[i][k] + d[k][j])

d[i][j] = d[i][k] + d[k][j];

int ans = INT_MIN;

for (int i = 0; i < N; ++i) {

if (d[K - 1][i] < 0) return -1;

ans = max(ans, d[K - 1][i]);

}

return ans;

}

};

// Author: Huahua

// Runtime: 89 ms

class Solution {

public:

int networkDelayTime(vector<vector<int>>& times, int N, int K) {

constexpr int MAX_TIME = 101 * 100;

vector<vector<int>> d(N, vector<int>(N, MAX_TIME));

for (auto time : times)

d[time[0] - 1][time[1] - 1] = time[2];

for (int i = 0; i < N; ++i)

d[i][i] = 0;

for (int k = 0; k < N; ++k)

for (int i = 0; i < N; ++i)

for (int j = 0; j < N; ++j)

d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

int max_time = *max_element(d[K - 1].begin(), d[K - 1].end());

return max_time >= MAX_TIME ? - 1 : max_time;

}

};

花花酱 LeetCode 399. Evaluate Division

By zxi on December 1, 2017

题目大意：给你一些含有变量名的分式的值，让你计算另外一些分式的值，如果不能计算返回-1。

Problem:

Equations are given in the format A / B = k, where A and B are variables represented as strings, and k is a real number (floating point number). Given some queries, return the answers. If the answer does not exist, return -1.0.

Example:
Given a / b = 2.0, b / c = 3.0.
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? .
return [6.0, 0.5, -1.0, 1.0, -1.0 ].

The input is: vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries , where equations.size() == values.size(), and the values are positive. This represents the equations. Return vector<double>.

According to the example above:

equations = [ ["a", "b"], ["b", "c"] ],

values = [2.0, 3.0],

queries = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ].

The input is always valid. You may assume that evaluating the queries will result in no division by zero and there is no contradiction.

Solution 1: DFS

C++

// Author: Huahua

// Runtime: 3 ms

class Solution {

public:

vector<double> calcEquation(vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries) {

// g[A][B] = k -> A / B = k

unordered_map<string, unordered_map<string, double>> g;

for (int i = 0; i < equations.size(); ++i) {

const string& A = equations[i].first;

const string& B = equations[i].second;

const double k = values[i];

g[A][B] = k;

g[B][A] = 1.0 / k;

}

vector<double> ans;

for (const auto& pair : queries) {

const string& X = pair.first;

const string& Y = pair.second;

if (!g.count(X) || !g.count(Y)) {

ans.push_back(-1.0);

continue;

}

unordered_set<string> visited;

ans.push_back(divide(X, Y, g, visited));

}

return ans;

}

private:

// get result of A / B

double divide(const string& A, const string& B,

unordered_map<string, unordered_map<string, double>>& g,

unordered_set<string>& visited) {

if (A == B) return 1.0;

visited.insert(A);

for (const auto& pair : g[A]) {

const string& C = pair.first;

if (visited.count(C)) continue;

double d = divide(C, B, g, visited); // d = C / B

// A / B = C / B * A / C

if (d > 0) return d * g[A][C];

}

return -1.0;

}

};

Java

// Updated: 2020/9/27

// Author: Huahua

// Running time: 1 ms

class Solution {

private Map<String, HashMap<String, Double>> g = new HashMap<>();

public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {

for (int i = 0; i < equations.size(); ++i) {

String x = equations.get(i).get(0);

String y = equations.get(i).get(1);

double k = values[i];

g.computeIfAbsent(x, l -> new HashMap<String, Double>()).put(y, k);

g.computeIfAbsent(y, l -> new HashMap<String, Double>()).put(x, 1.0 / k);

}

double[] ans = new double[queries.size()];

for (int i = 0; i < queries.size(); ++i) {

String x = queries.get(i).get(0);

String y = queries.get(i).get(1);

if (!g.containsKey(x) || !g.containsKey(y)) {

ans[i] = -1.0;

} else {

ans[i] = divide(x, y, new HashSet<String>());

}

return ans;

}

private double divide(String x, String y, Set<String> visited) {

if (x.equals(y)) return 1.0;

visited.add(x);

if (!g.containsKey(x)) return -1.0;

for (String n : g.get(x).keySet()) {

if (visited.contains(n)) continue;

visited.add(n);

double d = divide(n, y, visited);

if (d > 0) return d * g.get(x).get(n);

}

return -1.0;

}

Python3

"""

Author: Huahua

Running time: 32 ms (beats 100%)

"""

class Solution:

def calcEquation(self, equations, values, queries):

def divide(x, y, visited):

if x == y: return 1.0

visited.add(x)

for n in g[x]:

if n in visited: continue

visited.add(n)

d = divide(n, y, visited)

if d > 0: return d * g[x][n]

return -1.0

g = collections.defaultdict(dict)

for (x, y), v in zip(equations, values):

g[x][y] = v

g[y][x] = 1.0 / v

ans = [divide(x, y, set()) if x in g and y in g else -1 for x, y in queries]

return ans

Solution 2: Union Find

C++

// Author: Huahua

// Runtime: 3 ms

class Solution {

public:

vector<double> calcEquation(const vector<pair<string, string>>& equations, vector<double>& values, const vector<pair<string, string>>& queries) {

// parents["A"] = {"B", 2.0} -> A = 2.0 * B

// parents["B"] = {"C", 3.0} -> B = 3.0 * C

unordered_map<string, pair<string, double>> parents;

for (int i = 0; i < equations.size(); ++i) {

const string& A = equations[i].first;

const string& B = equations[i].second;

const double k = values[i];

// Neighter is in the forrest

if (!parents.count(A) && !parents.count(B)) {

parents[A] = {B, k};

parents[B] = {B, 1.0};

} else if (!parents.count(A)) {

parents[A] = {B, k};

} else if (!parents.count(B)) {

parents[B] = {A, 1.0 / k};

} else {

auto& rA = find(A, parents);

auto& rB = find(B, parents);

parents[rA.first] = {rB.first, k / rA.second * rB.second};

}

vector<double> ans;

for (const auto& pair : queries) {

const string& X = pair.first;

const string& Y = pair.second;

if (!parents.count(X) || !parents.count(Y)) {

ans.push_back(-1.0);

continue;

}

auto& rX = find(X, parents); // {rX, X / rX}

auto& rY = find(Y, parents); // {rY, Y / rY}

if (rX.first != rY.first)

ans.push_back(-1.0);

else // X / Y = (X / rX / (Y / rY))

ans.push_back(rX.second / rY.second);

}

return ans;

}

private:

pair<string, double>& find(const string& C, unordered_map<string, pair<string, double>>& parents) {

if (C != parents[C].first) {

const auto& p = find(parents[C].first, parents);

parents[C].first = p.first;

parents[C].second *= p.second;

}

return parents[C];

}

};

Java

// Updated: 9/27/2020

// Author: Huahua

// Running time: 3 ms

class Solution {

class Node {

public String parent;

public double ratio;

public Node(String parent, double ratio) {

this.parent = parent;

this.ratio = ratio;

}

class UnionFindSet {

private Map<String, Node> parents = new HashMap<>();

public Node find(String s) {

if (!parents.containsKey(s)) return null;

Node n = parents.get(s);

if (!n.parent.equals(s)) {

Node p = find(n.parent);

n.parent = p.parent;

n.ratio *= p.ratio;

}

return n;

}

public void union(String A, String B, double ratio) {

boolean hasA = parents.containsKey(A);

boolean hasB = parents.containsKey(B);

if (!hasA && !hasB) {

parents.put(A, new Node(B, ratio));

parents.put(B, new Node(B, 1.0));

} else if (!hasA) {

parents.put(A, new Node(B, ratio));

} else if (!hasB) {

parents.put(B, new Node(A, 1.0 / ratio));

} else {

Node rA = find(A);

Node rB = find(B);

parents.put(rA.parent,

new Node(rB.parent, ratio / rA.ratio * rB.ratio));

}

public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {

UnionFindSet u = new UnionFindSet();

for (int i = 0; i < equations.size(); ++i)

u.union(equations.get(i).get(0), equations.get(i).get(1), values[i]);

double[] ans = new double[queries.size()];

for (int i = 0; i < queries.size(); ++i) {

Node rx = u.find(queries.get(i).get(0));

Node ry = u.find(queries.get(i).get(1));

if (rx == null || ry == null || !rx.parent.equals(ry.parent))

ans[i] = -1.0;

else

ans[i] = rx.ratio / ry.ratio;

}

return ans;

}

Python3

"""

Author: Huahua

Running time: 32 ms (beats 100%)

"""

class Solution:

def calcEquation(self, equations, values, queries):

def find(x):

if x != U[x][0]:

px, pv = find(U[x][0])

U[x] = (px, U[x][1] * pv)

return U[x]

def divide(x, y):

rx, vx = find(x)

ry, vy = find(y)

if rx != ry: return -1.0

return vx / vy

U = {}

for (x, y), v in zip(equations, values):

if x not in U and y not in U:

U[x] = (y, v)

U[y] = (y, 1.0)

elif x not in U:

U[x] = (y, v)

elif y not in U:

U[y] = (x, 1.0 / v)

else:

rx, vx = find(x)

ry, vy = find(y)

U[rx] = (ry, v / vx * vy)

ans = [divide(x, y) if x in U and y in U else -1 for x, y in queries]

return ans

Related Problems:

花花酱 LeetCode 207. Course Schedule

By zxi on October 20, 2017

Problem:

There are a total of n courses you have to take, labeled from 0 to n - 1.

Some courses may have prerequisites, for example to take course 0 you have to first take course 1, which is expressed as a pair: [0,1]

Given the total number of courses and a list of prerequisite pairs, is it possible for you to finish all courses?

For example:

1	2, [[1,0]]

There are a total of 2 courses to take. To take course 1 you should have finished course 0. So it is possible.

1	2, [[1,0],[0,1]]

There are a total of 2 courses to take. To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

Idea:

Finding cycles O(n^2) -> Topological sort O(n)

Solution 1: Topological Sort

C++

// Author: Huahua

// Time complexity: O(n)

// Runtime: 12 ms

class Solution {

public:

bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {

graph_ = vector<vector<int>>(numCourses);

for(const auto& p : prerequisites)

graph_[p.first].push_back(p.second);

// states: 0 = unkonwn, 1 == visiting, 2 = visited

vector<int> v(numCourses, 0);

for(int i = 0; i < numCourses; ++i)

if(dfs(i, v)) return false;

return true;

}

private:

vector<vector<int>> graph_;

bool dfs(int cur, vector<int>& v) {

if(v[cur] == 1) return true;

if(v[cur] == 2) return false;

v[cur] = 1;

for(const int t : graph_[cur])

if(dfs(t, v)) return true;

v[cur] = 2;

return false;

}

};

Java

// Author: Huahua

// Runtime: 6 ms

// HashMap is slower than ArrayList in this problem.

class Solution {

public boolean canFinish(int numCourses, int[][] prerequisites) {

ArrayList<ArrayList<Integer>> graph = new ArrayList<>();

for (int i = 0; i < numCourses; ++i)

graph.add(new ArrayList<Integer>());

for (int i = 0; i < prerequisites.length; ++i) {

int course = prerequisites[i][0];

int prerequisite = prerequisites[i][1];

graph.get(course).add(prerequisite);

}

int[] visited = new int[numCourses];

for (int i = 0; i < numCourses; ++i)

if (dfs(i, graph, visited)) return false;

return true;

}

private boolean dfs(int curr, ArrayList<ArrayList<Integer>> graph, int[] visited) {

if (visited[curr] == 1) return true;

if (visited[curr] == 2) return false;

visited[curr] = 1;

for (int next : graph.get(curr))

if (dfs(next, graph, visited)) return true;

visited[curr] = 2;

return false;

}

Solution 2: DFS Finding cycles

Time complexity: O(n^2)

Space complexity: O(n)

C++

// Author: Huahua

// Time complexity: O(n^2)

// Runtime: 179 ms

class Solution {

public:

bool canFinish(int numCourses, vector<pair<int, int>>& prerequisites) {

graph_.clear();

for(const auto& p : prerequisites)

graph_[p.first].insert(p.second);

for (int i = 0; i < numCourses; ++i) {

vector<int> visited(numCourses, 0);

if (cycle(i, i, visited)) return false;

}

return true;

}

private:

unordered_map<int, unordered_set<int>> graph_;

bool cycle(int start, int curr, vector<int>& visited) {

if (curr == start && visited[start]) return true;

if (!graph_.count(curr)) return false;

for (const int next : graph_.at(curr)) {

if (visited[next]) continue;

visited[next] = true;

if (cycle(start, next, visited)) return true;

}

return false;

}

};

Related Pr0blems:

花花酱 LeetCode 126. Word Ladder II

By zxi on September 26, 2017

Problem:

Given two words (beginWord and endWord), and a dictionary’s word list, find all shortest transformation sequence(s) from beginWord to endWord, such that:

Only one letter can be changed at a time
Each transformed word must exist in the word list. Note that beginWord is not a transformed word.

For example,

Given:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log","cog"]

Return

[

["hit","hot","dot","dog","cog"],

["hit","hot","lot","log","cog"]

]

Note:

Return an empty list if there is no such transformation sequence.
All words have the same length.
All words contain only lowercase alphabetic characters.
You may assume no duplicates in the word list.
You may assume beginWord and endWord are non-empty and are not the same.

Idea:

BFS to construct the graph + DFS to extract the paths

Solutions:

C++, BFS 1

// Author: Huahua

// Running Time: 216 ms (better than 65.42%)

class Solution {

public:

vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {

unordered_set<string> dict(wordList.begin(), wordList.end());

if (!dict.count(endWord)) return {};

dict.erase(beginWord);

dict.erase(endWord);

unordered_map<string, int> steps{{beginWord, 1}};

unordered_map<string, vector<string>> parents;

queue<string> q;

q.push(beginWord);

vector<vector<string>> ans;

const int l = beginWord.length();

int step = 0;

bool found = false;

while (!q.empty() && !found) {

++step;

for (int size = q.size(); size > 0; size--) {

const string p = q.front(); q.pop();

string w = p;

for (int i = 0; i < l; i++) {

const char ch = w[i];

for (int j = 'a'; j <= 'z'; j++) {

if (j == ch) continue;

w[i] = j;

if (w == endWord) {

parents[w].push_back(p);

found = true;

} else {

// Not a new word, but another transform

// with the same number of steps

if (steps.count(w) && step < steps.at(w))

parents[w].push_back(p);

}

if (!dict.count(w)) continue;

dict.erase(w);

q.push(w);

steps[w] = steps.at(p) + 1;

parents[w].push_back(p);

}

w[i] = ch;

}

if (found) {

vector<string> curr{endWord};

getPaths(endWord, beginWord, parents, curr, ans);

}

return ans;

}

private:

void getPaths(const string& word,

const string& beginWord,

const unordered_map<string, vector<string>>& parents,

vector<string>& curr,

vector<vector<string>>& ans) {

if (word == beginWord) {

ans.push_back(vector<string>(curr.rbegin(), curr.rend()));

return;

}

for (const string& p : parents.at(word)) {

curr.push_back(p);

getPaths(p, beginWord, parents, curr, ans);

curr.pop_back();

}

};

C++ / BFS 2

// Author: Huahua

// Running time: 129 ms (better than 80.67%)

class Solution {

public:

vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {

vector<vector<string>> ans;

unordered_set<string> dict(wordList.begin(), wordList.end());

if (!dict.count(endWord)) return ans;

dict.erase(endWord);

const int l = beginWord.length();

unordered_set<string> q{beginWord}, p;

unordered_map<string, vector<string>> children;

bool found = false;

while (!q.empty() && !found) {

for (const string& word : q)

dict.erase(word);

for (const string& word : q) {

string curr = word;

for (int i = 0; i < l; i++) {

char ch = curr[i];

for (int j = 'a'; j <= 'z'; j++) {

curr[i] = j;

if (curr == endWord) {

found = true;

children[word].push_back(curr);

} else if (dict.count(curr) && !found) {

p.insert(curr);

children[word].push_back(curr);

}

curr[i] = ch;

}

std::swap(p, q);

p.clear();

}

if (found) {

vector<string> path{beginWord};

getPaths(beginWord, endWord, children, path, ans);

}

return ans;

}

private:

void getPaths(const string& word,

const string& endWord,

const unordered_map<string, vector<string>>& children,

vector<string>& path,

vector<vector<string>>& ans) {

if (word == endWord) {

ans.push_back(path);

return;

}

const auto it = children.find(word);

if (it == children.cend()) return;

for (const string& child : it->second) {

path.push_back(child);

getPaths(child, endWord, children, path, ans);

path.pop_back();

}

};

C++ / Bidirectional BFS

// Author: Huahua

// Running time: 39 ms (better than 93.74%)

class Solution {

public:

vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {

vector<vector<string>> ans;

unordered_set<string> dict(wordList.begin(), wordList.end());

if (!dict.count(endWord)) return ans;

int l = beginWord.length();

unordered_set<string> q1{beginWord};

unordered_set<string> q2{endWord};

unordered_map<string, vector<string>> children;

bool found = false;

bool backward = false;

while (!q1.empty() && !q2.empty() && !found) {

// Always expend the smaller queue first

if (q1.size() > q2.size()) {

std::swap(q1, q2);

backward = !backward;

}

for (const string& w : q1)

dict.erase(w);

for (const string& w : q2)

dict.erase(w);

unordered_set<string> q;

for (const string& word : q1) {

string curr = word;

for (int i = 0; i < l; i++) {

char ch = curr[i];

for (int j = 'a'; j <= 'z'; j++) {

curr[i] = j;

const string* parent = &word;

const string* child = &curr;

if (backward)

std::swap(parent, child);

if (q2.count(curr)) {

found = true;

children[*parent].push_back(*child);

} else if (dict.count(curr) && !found) {

q.insert(curr);

children[*parent].push_back(*child);

}

curr[i] = ch;

}

std::swap(q, q1);

}

if (found) {

vector<string> path{beginWord};

getPaths(beginWord, endWord, children, path, ans);

}

return ans;

}

private:

void getPaths(const string& word,

const string& endWord,

const unordered_map<string, vector<string>>& children,

vector<string>& path,

vector<vector<string>>& ans) {

if (word == endWord) {

ans.push_back(path);

return;

}

const auto it = children.find(word);

if (it == children.cend()) return;

for (const string& child : it->second) {

path.push_back(child);

getPaths(child, endWord, children, path, ans);

path.pop_back();

}

};

花花酱 LeetCode 332. Reconstruct Itinerary

By zxi on September 12, 2017

Problem:

Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.

Note:

If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
All airports are represented by three capital letters (IATA code).
You may assume all tickets form at least one valid itinerary.

Example 1:
tickets = [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Return ["JFK", "MUC", "LHR", "SFO", "SJC"].

Example 2:
tickets = [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Return ["JFK","ATL","JFK","SFO","ATL","SFO"].
Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"]. But it is larger in lexical order.

Idea:

Convert the graph to a tree and do post-order traversal

Solution:

// Author: Huahua

// Running time: 13 ms

class Solution {

public:

vector<string> findItinerary(vector<pair<string, string>> tickets) {

route_.clear();

trips_.clear();

for(const auto& pair : tickets)

trips_[pair.first].push_back(pair.second);

for(auto& pair : trips_) {

auto& dests = pair.second;

std::sort(dests.begin(), dests.end());

}

const string kStart = "JFK";

visit(kStart);

return vector<string>(route_.crbegin(), route_.crend());

}

private:

// src -> {dst1, dest2, ..., destn}

unordered_map<string, deque<string>> trips_;

// ans (reversed)

vector<string> route_;

void visit(const string& src) {

auto& dests = trips_[src];

while (!dests.empty()) {

// Get the smallest dest

const string dest = dests.front();

// Remove the ticket

dests.pop_front();

// Visit dest

visit(dest);

}

// Add current node to the route

route_.push_back(src);

}

};