Posts tagged as “grid”

花花酱 LeetCode 994. Rotting Oranges

By zxi on February 16, 2019

In a given grid, each cell can have one of three values:

the value 0 representing an empty cell;
the value 1 representing a fresh orange;
the value 2 representing a rotten orange.

Every minute, any fresh orange that is adjacent (4-directionally) to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1instead.

Example 1:

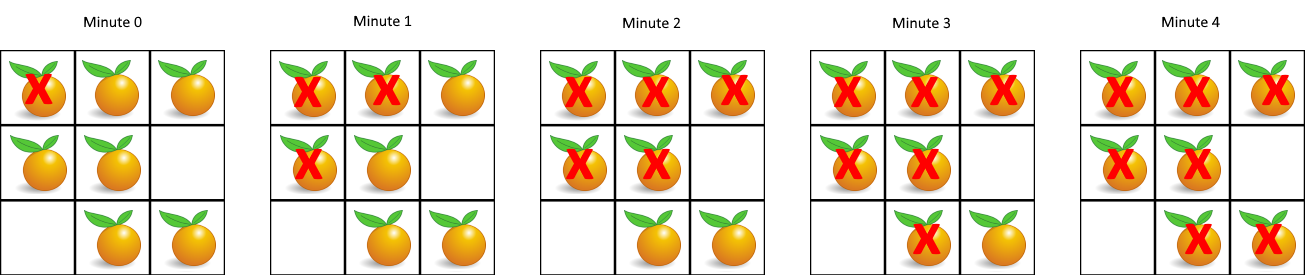
Input: [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation:  The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: [[0,2]]
Output: 0
Explanation:  Since there are already no fresh oranges at minute 0, the answer is just 0.

Note:

1 <= grid.length <= 10
1 <= grid[0].length <= 10
grid[i][j] is only 0, 1, or 2.

Solution: BFS

Time complexity: O(mn)
Space complexity: O(mn)

C++

// Author: Huahua, Running time: 12 ms, 10.8 MB

class Solution {

public:

int orangesRotting(vector<vector<int>>& grid) {

const int m = grid.size();

const int n = grid[0].size();

queue<pair<int,int>> q;

int fresh = 0;

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j)

if (grid[i][j] == 1) ++fresh;

else if (grid[i][j] == 2) q.emplace(j, i);

vector<int> dirs = {1, 0, -1, 0, 1};

int days = 0;

while (!q.empty() && fresh) {

int size = q.size();

while (size--) {

int x = q.front().first;

int y = q.front().second;

q.pop();

for (int i = 0; i < 4; ++i) {

int dx = x + dirs[i];

int dy = y + dirs[i + 1];

if (dx < 0 || dx >= n || dy < 0 || dy >= m || grid[dy][dx] != 1) continue;

--fresh;

grid[dy][dx] = 2;

q.emplace(dx, dy);

}

++days;

}

return fresh ? -1 : days;

}

};

花花酱 LeetCode 85. Maximal Rectangle

By zxi on January 26, 2019

Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.

Example:

Input:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
Output: 6

Solution: DP

Time complexity: O(m^2*n)
Space complexity: O(mn)

dp[i][j] := max length of all 1 sequence ends with col j, at the i-th row.
transition:
dp[i][j] = 0 if matrix[i][j] == ‘0’
= dp[i][j-1] + 1 if matrix[i][j] == ‘1’

C++

class Solution {

public:

int maximalRectangle(vector<vector<char> > &matrix) {

int r = matrix.size();

if (r == 0) return 0;

int c = matrix[0].size();

// dp[i][j] := max len of all 1s ends with col j at row i.

vector<vector<int>> dp(r, vector<int>(c));

for (int i = 0; i < r; ++i)

for (int j = 0; j < c; ++j)

dp[i][j] = (matrix[i][j] == '1') ? (j == 0 ? 1 : dp[i][j - 1] + 1) : 0;

int ans = 0;

for (int i = 0; i < r; ++i)

for (int j = 0; j < c; ++j) {

int len = INT_MAX;

for (int k = i; k < r; k++) {

len = min(len, dp[k][j]);

if (len == 0) break;

ans = max(len * (k - i + 1), ans);

}

return ans;

}

};

花花酱 LeetCode 463. Island Perimeter

By zxi on August 17, 2018

Problem

You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 represents water. Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells). The island doesn’t have “lakes” (water inside that isn’t connected to the water around the island). One cell is a square with side length 1. The grid is rectangular, width and height don’t exceed 100. Determine the perimeter of the island.

Example:

[[0,1,0,0],
 [1,1,1,0],
 [0,1,0,0],
 [1,1,0,0]]

Answer: 16
Explanation: The perimeter is the 16 yellow stripes in the image below:

Solution: Counting

If a land has 0 neighbour, it contributes 4 to the perimeter

If a land has 1 neighbour, it contributes 3 to the perimeter

If a land has 2 neighbours, it contributes 2 to the perimeter

If a land has 3 neighbours, it contributes 1 to the perimeter

If a land has 4 neighbours, it contributes 0 to the perimeter

perimeter = area * 4 – total_neighbours

Time complexity: O(mn)

Space complexity: O(1)

// Author: Huahua

// Running time: 148 ms

class Solution {

public:

int islandPerimeter(vector<vector<int>>& grid) {

if (grid.empty()) return 0;

int m = grid.size();

int n = grid[0].size();

int area = 0;

int conn = 0;

for (int y = 0; y < m; ++y)

for (int x = 0; x < n; ++x)

if (grid[y][x] == 1) {

++area;

if (y > 0 && grid[y - 1][x] == 1) ++conn;

if (x > 0 && grid[y][x - 1] == 1) ++conn;

}

return area*4 - conn*2;

}

};

花花酱 LeetCode 174. Dungeon Game

By zxi on August 16, 2018

Problem

The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0’s) or contain magic orbs that increase the knight’s health (positive integers).

In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Write a function to determine the knight’s minimum initial health so that he is able to rescue the princess.

For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path RIGHT-> RIGHT -> DOWN -> DOWN.

-2 (K)	-3	3
-5	-10	1
10	30	-5 (P)

Note:

The knight’s health has no upper bound.
Any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

Solution: DP

Time complexity: O(mn)

Space complexity: O(mn) -> O(n)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int calculateMinimumHP(vector<vector<int>>& dungeon) {

const int m = dungeon.size();

const int n = dungeon[0].size();

// hp[y][x]: min hp required to reach bottom right (P).

vector<vector<int>> hp(m + 1, vector<int>(n + 1, INT_MAX));

hp[m][n - 1] = hp[m - 1][n] = 1;

for (int y = m - 1; y >= 0; --y)

for (int x = n - 1; x >= 0; --x)

hp[y][x] = max(1, min(hp[y + 1][x], hp[y][x + 1]) - dungeon[y][x]);

return hp[0][0];

}

};

O(n) space

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int calculateMinimumHP(vector<vector<int>>& dungeon) {

const int m = dungeon.size();

const int n = dungeon[0].size();

// hp[y][x]: min hp required to reach bottom right (P).

vector<int> hp(n + 1, INT_MAX);

hp[n - 1] = 1;

for (int y = m - 1; y >= 0; --y)

for (int x = n - 1; x >= 0; --x)

hp[x] = max(1, min(hp[x], hp[x + 1]) - dungeon[y][x]);

return hp[0];

}

};

花花酱 LeetCode 864. Shortest Path to Get All Keys

By zxi on July 8, 2018

Problem

We are given a 2-dimensional grid. "." is an empty cell, "#" is a wall, "@" is the starting point, ("a", "b", …) are keys, and ("A", "B", …) are locks.

We start at the starting point, and one move consists of walking one space in one of the 4 cardinal directions. We cannot walk outside the grid, or walk into a wall. If we walk over a key, we pick it up. We can’t walk over a lock unless we have the corresponding key.

For some 1 <= K <= 6, there is exactly one lowercase and one uppercase letter of the first K letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it’s impossible, return -1.

Example 1:

Input: ["@.a.#","###.#","b.A.B"]
Output: 8

Example 2:

Input: ["@..aA","..B#.","....b"]
Output: 6

Note:

1 <= grid.length <= 30
1 <= grid[0].length <= 30
grid[i][j] contains only '.', '#', '@', 'a'-'f' and 'A'-'F'
The number of keys is in [1, 6]. Each key has a different letter and opens exactly one lock.

Solution: BFS

Time complexity: O(m*n*64)

Space complexity: O(m*n*64)

C++

// Author: Huahua

// Running time: 8 ms

class Solution {

public:

int shortestPathAllKeys(vector<string>& grid) {

int m = grid.size();

int n = grid[0].size();

int all_keys = 0;

queue<int> q;

vector<vector<vector<int>>> seen(m, vector<vector<int>>(n, vector<int>(64, 0)));

// Init

for (int i = 0; i < m; ++i)

for (int j = 0; j < n; ++j) {

const char c = grid[i][j];

if (c == '@') {

q.push((j << 16) | (i << 8));

seen[i][j][0] = 1;

} else if (c >= 'a' && c <= 'f') {

all_keys |= (1 << (c - 'a'));

}

const vector<int> dirs{-1, 0, 1, 0, -1};

int steps = 0;

while (!q.empty()) {

int size = q.size();

while (size--) {

int s = q.front(); q.pop();

int x = s >> 16;

int y = (s >> 8) & 0xFF;

int keys = s & 0xFF;

if (keys == all_keys) return steps;

for (int i = 0; i < 4; ++i) {

int nkeys = keys;

int nx = x + dirs[i];

int ny = y + dirs[i + 1];

if (nx < 0 || nx >= n || ny < 0 || ny >= m) continue;

const char c = grid[ny][nx];

if (c == '#') continue; // Wall

// Do not have the key.

if (c >= 'A' && c <= 'F' && !(keys & (1 << (c - 'A')))) continue;

// Update the keys we have.

if (c >= 'a' && c <= 'f') nkeys |= (1 << (c - 'a'));

if (seen[ny][nx][nkeys]) continue;

q.push((nx << 16) | (ny << 8) | nkeys);

seen[ny][nx][nkeys] = 1;

}

++steps;

}

return -1;

}

};

Python3

# Author: Huahua, 390 ms

class Solution:

def shortestPathAllKeys(self, grid):

m, n = len(grid), len(grid[0])

all_keys = 0

seen = [[[None]* 64 for _ in range(n)] for _ in range(m)]

q = collections.deque()

for i in range(m):

for j in range(n):

c = grid[i][j]

if c == '@':

q.append((j << 16) | (i << 8))

seen[i][j][0] = 1

elif c >= 'a' and c <= 'f':

all_keys |= (1 << (ord(c) - ord('a')))

dirs = [-1, 0, 1, 0, -1]

steps = 0

while q:

size = len(q)

while size > 0:

size -= 1

s = q.popleft()

x = s >> 16

y = (s >> 8) & 0xff

keys = s & 0xff

if keys == all_keys: return steps

for i in range(4):

nx, ny, nkeys = x + dirs[i], y + dirs[i + 1], keys

if nx < 0 or nx >= n or ny < 0 or ny >= m: continue

c = grid[ny][nx]

if c == '#': continue

if c in string.ascii_uppercase and keys & (1 << (ord(c) - ord('A'))) == 0: continue

if c in string.ascii_lowercase: nkeys |= (1 << (ord(c) - ord('a')))

if seen[ny][nx][nkeys]: continue

q.append((nx << 16) | (ny << 8) | nkeys)

seen[ny][nx][nkeys] = 1

steps += 1

return -1

Posts tagged as “grid”

花花酱 LeetCode 994. Rotting Oranges

Solution: BFS

C++

花花酱 LeetCode 85. Maximal Rectangle

Solution: DP

C++

花花酱 LeetCode 463. Island Perimeter

Problem

Solution: Counting

花花酱 LeetCode 174. Dungeon Game

Problem

Solution: DP

花花酱 LeetCode 864. Shortest Path to Get All Keys

Problem

Solution: BFS

C++

Python3

Related Problems