Posts tagged as “knapsack”

Knapsack Problem 背包问题

By zxi on November 10, 2018

Videos

上期节目中我们对动态规划做了一个总结，这期节目我们来聊聊背包问题。

背包问题是一个NP-complete的组合优化问题，Search的方法需要O(2^N)时间才能获得最优解。而使用动态规划，我们可以在伪多项式（pseudo-polynomial time）时间内获得最优解。

0-1 Knapsack Problem 0-1背包问题

Problem

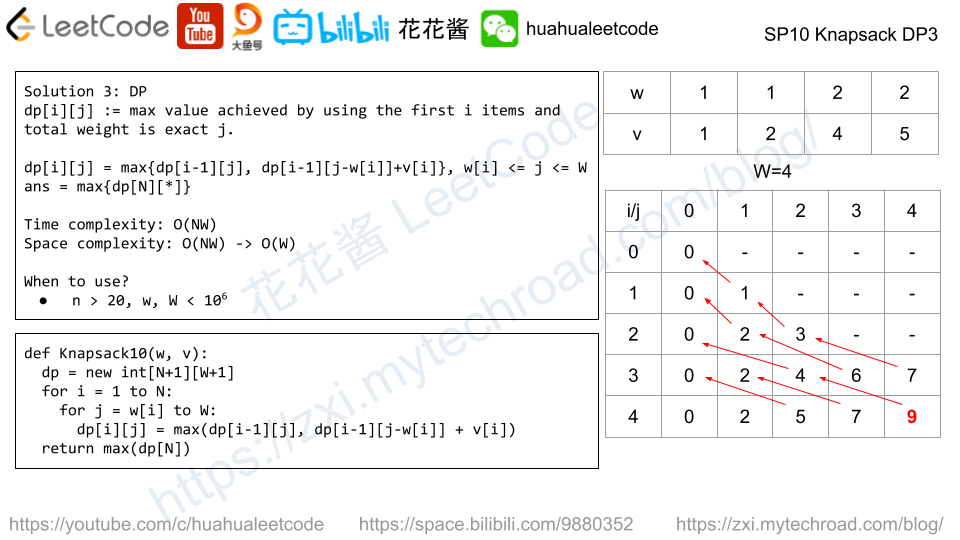
Given N items, w[i] is the weight of the i-th item and v[i] is value of the i-th item. Given a knapsack with capacity W. Maximize the total value. Each item can be use 0 or 1 time.

0-1背包问题的通常定义是：一共有N件物品，第i件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够获得的最大价值是多少？每件物品可以使用0次或者1次。

例子：

重量 w = [1, 1, 2, 2]

价值 v = [1, 3, 4, 5]

背包承重 W = 4

最大价值为9，可以选第1,2,4件物品，也可以选第3，4件物品；总重量为4，总价值为9。

动态规划的状态转移方程为：

1	dp[i][j] = max(dp[i-1][j], dp[i][j-w[i]] + v[i])

Solutions

Search

def knapsack01DFS(w, v, W):

def dfs(s, cur_w, cur_v, ans):

ans[0] = max(ans[0], cur_v)

if s == N: return

for i in range(s, N):

if cur_w + w[i] <= W:

dfs(i + 1, cur_w + w[i], cur_v + v[i], ans)

ans = [0]

dfs(0, 0, 0, ans)

return ans[0]

DP2

def knapsack01(w, v, W):

dp = [[0] * (W + 1) for _ in range(N+1)]

for i in range(1, N + 1):

dp[i] = dp[i-1].clone()

for j in range(w[i], W + 1):

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1])

return max(dp[N])

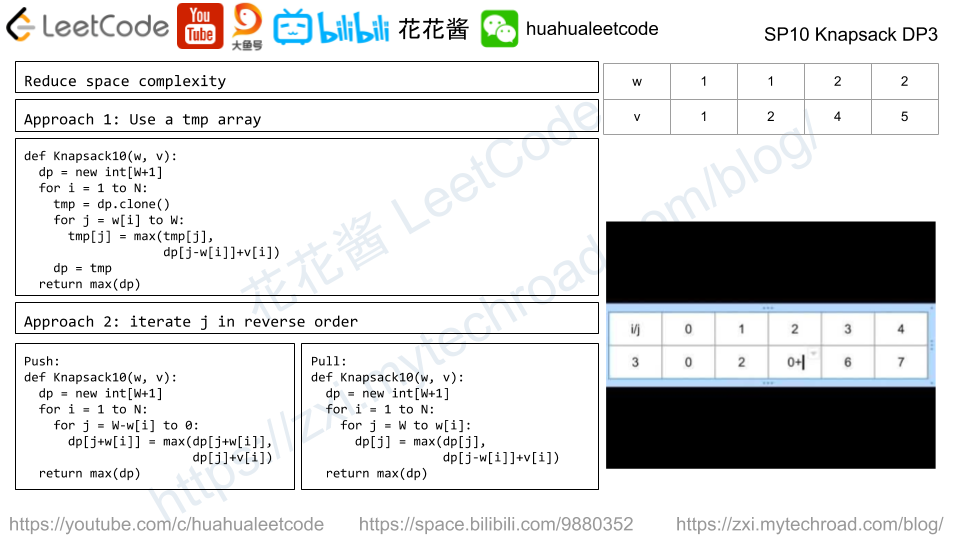
DP1/tmp

def knapsack01R(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

tmp = list(dp)

for j in range(w[i], W + 1):

tmp[j] = max(tmp[j], dp[j - w[i]] + v[i])

dp = tmp

return max(dp)

DP1/push

def knapsack01R2(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

for j in range(W, w[i] - 1, -1):

dp[j] = max(dp[j], dp[j - w[i]] + v[i])

return max(dp)

DP1/pull

def knapsack01R1(w, v, W):

dp = [0] * (W + 1)

for i in range(0, N):

for j in range(W - w[i], -1, -1):

dp[j + w[i]] = max(dp[j + w[i]], dp[j] + v[i])

return max(dp)

Unbounded Knapsack Problem 完全背包

完全背包、多重背包是常见的变形。和01背包的区别在于，完全背包每件物品可以使用无限多次，而多重背包每件物品最多可以使用n[i]次。两个问题都可以转换成01背包问题进行求解。

但是Naive的转换会大大增加时间复杂度：

完全背包：“复制”第i件物品到一共有 W/w[i] 件

多重背包：“复制”第i件物品到一共有 n[i] 件

然后直接调用01背包进行求解。

时间复杂度：

完全背包 O(Σ(W/w[i])*W)

多重背包 O(Σn[i]*W)

不难看出时间复杂度 = O(物品数量*背包承重)

背包承重是给定的，要降低运行时候，只有减少物品数量。但怎样才能减少总的物品数量呢？

这就涉及到二进制思想：任何一个正整数都可以用 (1, 2, 4, …, 2^K)的组合来表示。例如14 = 2 + 4 + 8。
原本需要放入14件相同的物品，现在只需要放入3件（重量和价值是原物品的2倍，4倍，8倍）。大幅降低了总的物品数量从而降低运行时间。

完全背包：对于第i件物品，我们只需要创建k = log(W/w[i])件虚拟物品即可。

每件虚拟物品的重量和价值为：1*(w[i], v[i]), 2*(w[i], v[i]), …, 2^k*(w[i], v[i])。

多重背包：对于第i件物品，我们只需要创建k + 1件虚拟物品即可，其中k = log(n[i])。

每件虚拟物品的重量和价值为：1*(w[i], v[i]), 2*(w[i], v[i]), …, 2^(k-1)*(w[i], v[i]), 以及 (n[i] – 2^k – 1) * (w[i], v[i])。

例如：n[i] = 14, k = 3, 虚拟物品的倍数为 1, 2, 4 和 7，这4个数组合可以组成1 ~ 14中的任何一个数，并且不会>14，即不超过n[i]。

二进制转换后直接调用01背包即可

时间复杂度：

完全背包 O(Σlog(W/w[i])*W)

多重背包 O(Σlog(n[i])*W)

空间复杂度 O(W)

其实完全背包和多重背包都可以在 O(NW)时间内完成，前者在视频中有讲到，后者属于超纲内容，以后有机会再和大家深入分享。

Bounded Knapsack Problem 多重背包

花花酱 LeetCode 871. Minimum Number of Refueling Stops

By zxi on July 14, 2018

Problem

A car travels from a starting position to a destination which is target miles east of the starting position.

Along the way, there are gas stations. Each station[i] represents a gas station that is station[i][0] miles east of the starting position, and has station[i][1] liters of gas.

The car starts with an infinite tank of gas, which initially has startFuel liters of fuel in it. It uses 1 liter of gas per 1 mile that it drives.

When the car reaches a gas station, it may stop and refuel, transferring all the gas from the station into the car.

What is the least number of refueling stops the car must make in order to reach its destination? If it cannot reach the destination, return -1.

Note that if the car reaches a gas station with 0 fuel left, the car can still refuel there. If the car reaches the destination with 0 fuel left, it is still considered to have arrived.

Example 1:

Input: target = 1, startFuel = 1, stations = []
Output: 0
Explanation: We can reach the target without refueling.

Example 2:

Input: target = 100, startFuel = 1, stations = [[10,100]]
Output: -1
Explanation: We can't reach the target (or even the first gas station).

Example 3:

Input: target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
Output: 2
Explanation: 
We start with 10 liters of fuel.
We drive to position 10, expending 10 liters of fuel.  We refuel from 0 liters to 60 liters of gas.
Then, we drive from position 10 to position 60 (expending 50 liters of fuel),
and refuel from 10 liters to 50 liters of gas.  We then drive to and reach the target.
We made 2 refueling stops along the way, so we return 2.

Note:

1 <= target, startFuel, stations[i][1] <= 10^9
0 <= stations.length <= 500
0 < stations[0][0] < stations[1][0] < ... < stations[stations.length-1][0] < target

Solution1: DP

Time complexity: O(n^2)

Space complexity: O(n)

C++

// Author: Huahua

// Running time: 24 ms

class Solution {

public:

int minRefuelStops(int target, int startFuel, vector<vector<int>>& stations) {

const int n = stations.size();

// dp[i]: max distance to go with i stops.

vector<long> dp(n + 1, startFuel);

// For each station

for (int i = 0; i < n; ++i)

// for j stops, start from high to low to avoid reusing station i

for (int j = i + 1; j >= 1; --j)

if (dp[j - 1] >= stations[i][0])

// if we can reach station i with j - 1 stops,

// we can reach dp[j - 1] + station[i][1] with j stops.

dp[j] = max(dp[j], dp[j - 1] + stations[i][1]);

for (int i = 0; i < dp.size(); ++i)

if (dp[i] >= target) return i;

return -1;

}

};

Solution2: Priority Queue

Time complexity: O(nlogn)

Space complexity: O(n)

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

int minRefuelStops(int target, int startFuel, vector<vector<int>>& stations) {

int cur = startFuel;

int stops = 0;

int i = 0;

priority_queue<int> q; // gas (high to low) of reachable stations.

while (true) {

if (cur >= target) return stops;

while (i < stations.size() && stations[i][0] <= cur)

q.push(stations[i++][1]);

if (q.empty()) break;

cur += q.top(); q.pop();

++stops;

}

return -1;

}

};

V2: Iterator

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

int minRefuelStops(int target, int startFuel, vector<vector<int>>& stations) {

int cur = startFuel;

int stops = 0;

priority_queue<int> q; // gas (high to low) of reachable stations.

auto it = begin(stations);

while (true) {

if (cur >= target) return stops;

while (it != end(stations) && it->at(0) <= cur)

q.push(it++->at(1));

if (q.empty()) break;

cur += q.top(); q.pop();

++stops;

}

return -1;

}

};

Related Problems

花花酱 LeetCode 322. Coin Change

花花酱 LeetCode 518. Coin Change 2

By zxi on March 2, 2018

题目大意：给你一些硬币的面值，问使用这些硬币（无限多块）能够组成amount的方法有多少种。

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.

Note: You can assume that

0 <= amount <= 5000
1 <= coin <= 5000
the number of coins is less than 500
the answer is guaranteed to fit into signed 32-bit integer

Example 1:

Input: amount = 5, coins = [1, 2, 5]

Output: 4

Explanation: there are four ways to make up the amount:

5=5

5=2+2+1

5=2+1+1+1

5=1+1+1+1+1

Example 2:

Input: amount = 3, coins = [2]

Output: 0

Explanation: the amount of 3 cannot be made up just with coins of 2.

Example 3:

1 2	Input: amount = 10, coins = [10] Output: 1

Idea: DP

Transition 1:

Let us use dp[i][j] to denote the number of ways to sum up to amount j using first i kind of coins.

dp[i][j] = dp[i – 1][j – coin] + dp[i – 1][j – 2* coin] + …

Time complexity: O(n*amount^2) TLE

Space complexity: O(n*amount) -> O(amount)

Transition 2:

Let us use dp[i] to denote the number of ways to sum up to amount i.

dp[i + coin] += dp[i]

Time complexity: O(n*amount)

Space complexity: O(amount)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

int change(int amount, vector<int>& coins) {

vector<int> dp(amount + 1, 0);

dp[0] = 1;

for (const int coin : coins)

for (int i = 0; i <= amount - coin; ++i)

dp[i + coin] += dp[i];

return dp[amount];

}

};

Java

// Author: Huahua

// Running time: 7 ms

class Solution {

public int change(int amount, int[] coins) {

int[] dp = new int[amount + 1];

dp[0] = 1;

for (int coin : coins)

for (int i = 0; i <= amount - coin; ++i)

dp[i + coin] += dp[i];

return dp[amount];

}

Python

"""

Author: Huahua

Running time: 107 ms (beats 100%)

"""

class Solution(object):

def change(self, amount, coins):

dp = [1] + [0] * (amount);

for coin in coins:

for i in xrange(amount - coin + 1):

if dp[i]:

dp[i + coin] += dp[i]

return dp[amount]

Related Problems:

花花酱 LeetCode 322. Coin Change

花花酱 LeetCode 322. Coin Change

By zxi on January 2, 2018

题目大意：给你一些不同币值的硬币，问你最少需要多少个硬币才能组成amount，假设每种硬币有无穷多个。

Problem:

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

Example 1:
coins = [1, 2, 5], amount = 11
return 3 (11 = 5 + 5 + 1)

Example 2:
coins = [2], amount = 3
return -1.

Idea:

DP /knapsack

Solution1:

C++ / DP

Time complexity: O(n*amount^2)

Space complexity: O(amount)

// Author: Huahua

// Running time: 189 ms

class Solution {

public:

int coinChange(vector<int>& coins, int amount) {

vector<int> dp(amount + 1, INT_MAX);

dp[0] = 0;

for (auto coin : coins) {

for (int i = amount - coin; i >= 0; --i)

if (dp[i] != INT_MAX)

for (int k = 1; k * coin + i <= amount; ++k)

dp[i + k * coin] = min(dp[i + k * coin], dp[i] + k);

}

return dp[amount] == INT_MAX ? -1 : dp[amount];

}

};

Solution2:

C++ / DP

Time complexity: O(n*amount)

Space complexity: O(amount)

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

int coinChange(vector<int>& coins, int amount) {

// dp[i] = min coins to make up to amount i

vector<int> dp(amount + 1, INT_MAX);

dp[0] = 0;

for (int coin : coins) {

for (int i = coin; i <= amount; ++i)

if (dp[i - coin] != INT_MAX)

dp[i] = min(dp[i], dp[i - coin] + 1);

}

return dp[amount] == INT_MAX ? -1 : dp[amount];

}

};

Python3

"""

Author: Huahua

Running time: 632 ms beats 90.27%

"""

class Solution:

def coinChange(self, coins, amount):

INVALID = 2**32

dp = [INVALID] * (amount + 1)

dp[0] = 0

for coin in coins:

for i in range(coin, amount + 1):

if dp[i - coin] >= dp[i]: continue

dp[i] = dp[i - coin] + 1

return -1 if dp[amount] == INVALID else dp[amount]

Solution3:

C++ / DFS

Time complexity: O(amount^n/(coin_0*coin_1*…*coin_n))

Space complexity: O(n)

// Author: Huahua

// Running time: 6 ms

class Solution {

public:

int coinChange(vector<int>& coins, int amount) {

// Sort coins in desending order

std::sort(coins.rbegin(), coins.rend());

int ans = INT_MAX;

coinChange(coins, 0, amount, 0, ans);

return ans == INT_MAX ? -1 : ans;

}

private:

void coinChange(const vector<int>& coins,

int s, int amount, int count, int& ans) {

if (amount == 0) {

ans = min(ans, count);

return;

}

if (s == coins.size()) return;

const int coin = coins[s];

for (int k = amount / coin; k >= 0 && count + k < ans; k--)

coinChange(coins, s + 1, amount - k * coin, count + k, ans);

}

};

Python3

"""

Author: Huahua

Running time: 200ms

"""

class Solution:

def coinChange(self, coins, amount):

coins.sort(reverse=True)

INVALID = 10**10

self.ans = INVALID

def dfs(s, amount, count):

if amount == 0:

self.ans = count

return

if s == len(coins): return

coin = coins[s]

for k in range(amount // coin, -1, -1):

if count + k >= self.ans: break

dfs(s + 1, amount - k * coin, count + k)

dfs(0, amount, 0)

return -1 if self.ans == INVALID else self.ans

花花酱 LeetCode 416. Partition Equal Subset Sum

By zxi on December 31, 2017

题目大意：

给你一个正整数的数组，问你能否把元素划分成元素和相等的两组。

Problem:

Given a non-empty array containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

Note:

Each of the array element will not exceed 100.
The array size will not exceed 200.

Example 1:

Input: [1, 5, 11, 5]

Output: true

Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

Input: [1, 2, 3, 5]

Output: false

Explanation: The array cannot be partitioned into equal sum subsets.

Idea:

DP 动态规划

Solution:

Time complexity: O(n*sum)

Space complexity: O(sum)

C++

// Author: Huahua

// Running time: 16 ms

class Solution {

public:

bool canPartition(vector<int>& nums) {

const int sum = std::accumulate(nums.begin(), nums.end(), 0);

if (sum % 2 != 0) return false;

vector<int> dp(sum + 1, 0);

dp[0] = 1;

for (const int num : nums) {

for (int i = sum; i >= 0; --i)

if (dp[i]) dp[i + num] = 1;

if (dp[sum / 2]) return true;

}

return false;

}

};