Posts tagged as “math”

花花酱 LeetCode. 69 Sqrt(x)

By zxi on January 16, 2018

题目大意：让你实现开根号函数，只需要返回整数部分。

Problem:

Implement int sqrt(int x).

Compute and return the square root of x.

x is guaranteed to be a non-negative integer.

Example 1:

1 2	Input: 4 Output: 2

Example 2:

Input: 8

Output: 2

Explanation: The square root of 8 is 2.82842...

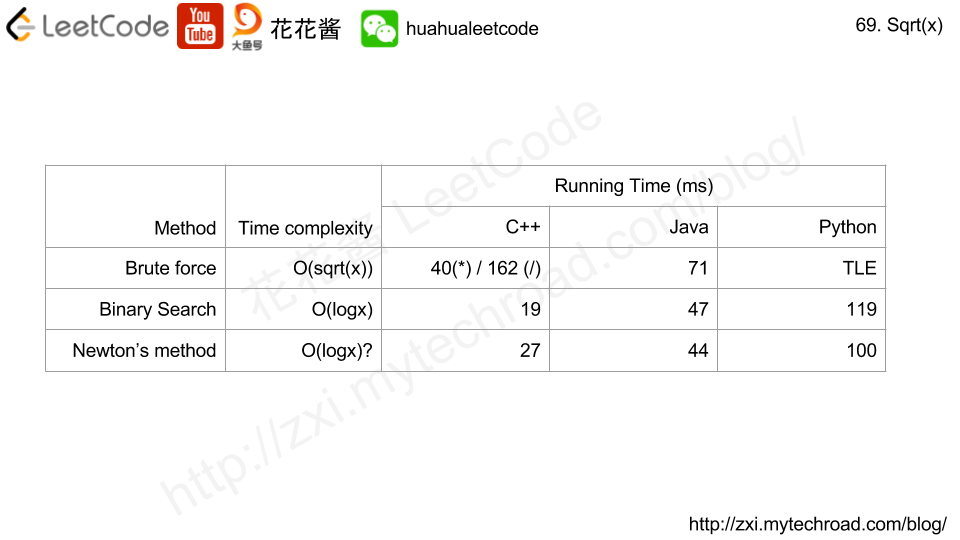
Solution 1: Brute force

Time complexity: sqrt(x)

C++

// Author: Huahua

// Running time: 40 ms

class Solution {

public:

int mySqrt(int x) {

if (x <= 1) return x;

for (long long s = 1; s <= x; ++s)

if (s * s > x) return s - 1;

return -1;

}

};

C++ div

// Author: Huahua

// Running time: 162 ms

class Solution {

public:

int mySqrt(int x) {

if (x <= 1) return x;

for (int s = 1; s <= x; ++s)

if (s > x / s) return s - 1;

return -1;

}

};

Java

// Author: Huahua

// Running time: 71 ms

class Solution {

public int mySqrt(int x) {

if (x <= 1) return x;

for (long s = 1; s <= x; ++s)

if (s * s > x) return (int)s - 1;

return -1;

}

Python3 TLE

"""

Author: Huahua

TLE: 602 / 1017 test cases passed.

"""

class Solution:

def mySqrt(self, x):

if x <= 1: return x

s = 1

while True:

if s*s > x: return s - 1

s += 1

return -1

Solution 2: Binary search

Time complexity: O(logn)

C++

// Author: Huahua

// Running time: 12 ms

class Solution {

public:

int mySqrt(int x) {

long l = 1;

long r = static_cast<long>(x) + 1;

while (l < r) {

long m = l + (r - l) / 2;

if (m * m > x) {

r = m;

} else {

l = m + 1;

}

// l: smallest number such that l * l > x

return l - 1;

}

};

Java

// Author: Huahua

// Running time: 47 ms

class Solution {

public int mySqrt(int x) {

int l = 1;

int r = x;

while (l <= r) {

int m = l + (r - l) / 2;

if (m > x / m) {

r = m - 1;

} else {

l = m + 1;

}

return r;

}

Python3

"""

Author: Huahua

Running time: 119 ms

"""

class Solution:

def mySqrt(self, a):

l = 1

r = a

while l <= r:

m = l + (r - l) // 2

if m * m > a:

r = m - 1

else:

l = m + 1

return r;

Solution 3: Newton’s method

C++ / float

// Author: Huahua

// Running time: 28 ms

class Solution {

public:

int mySqrt(int a) {

constexpr double epsilon = 1e-2;

double x = a;

while (x * x - a > epsilon) {

x = (x + a / x) / 2.0;

}

return x;

}

};

C++ / int

// Author: Huahua

// Running time: 27 ms

class Solution {

public:

int mySqrt(int a) {

// f(x) = x^2 - a, find root of f(x)

// Newton's method

// f'(x) = 2x

// x' = x - f(x) / f'(x) = x - (1/2*x - a/(2*x))

// = (x + a / x) / 2

int x = a;

while (x > a / x)

x = (x + a / x) / 2;

return x;

}

};

Java

// Author: Huahua

// Running time: 44 ms

class Solution {

public int mySqrt(int a) {

long x = a;

while (x * x > a)

x = (x + a / x) / 2;

return (int)x;

}

Python3

"""

Author: Huahua

Running time: 100 ms

"""

class Solution:

def mySqrt(self, a):

x = a

while x * x > a:

x = (x + a // x) // 2

return x

花花酱 LeetCode 754. Reach a Number

By zxi on January 1, 2018

题目大意：第i时刻可以移动+i,-i单位距离。初始在原点，问最少对少时间可以移动到target坐标。

Problem:

You are standing at position 0 on an infinite number line. There is a goal at position target.

On each move, you can either go left or right. During the n-th move (starting from 1), you take n steps.

Return the minimum number of steps required to reach the destination.

Example 1:

Input: target = 3

Output: 2

Explanation:

On the first move we step from 0 to 1.

On the second step we step from 1 to 3.

Example 2:

Input: target = 2

Output: 3

Explanation:

On the first move we step from 0 to 1.

On the second move we step from 1 to -1.

On the third move we step from -1 to 2.

Note:

target will be a non-zero integer in the range [-10^9, 10^9].

Idea:

Math

Time complexity: O(sqrt(target))

Space complexity: O(1)

// Author: Huahua

// Running time: 3 ms

class Solution {

public:

int reachNumber(int target) {

target = std::abs(target);

int k = 0;

int sum = 0;

while (sum < target) sum += (++k);

const int d = sum - target;

if (d % 2 == 0) return k;

return k + 1 + (k % 2);

}

};

O(1)

// Author: Huahua

// Running time: 3 ms

class Solution {

public:

int reachNumber(int target) {

target = std::abs(target);

int k = sqrt(target * 2);

while (sum(k) < target) ++k;

int d = sum(k) - target;

if (d % 2 == 0) return k;

return k + 1 + (k % 2);

}

private:

int sum(int k) {

return k * (k + 1) / 2;

}

};

花花酱 LeetCode 204. Count Primes

By zxi on September 9, 2017

Problem:

Count the number of prime numbers less than a non-negative number, n.

Idea:

Sieve of Eratosthenes

Time Complexity:

O(nloglogn)

Space Complexity:

O(n)

Solution:

C++

// Author: Huahua

class Solution {

public:

int countPrimes(int n) {

if (n < 3) return 0;

vector<unsigned char> f(n, 1);

f[0] = f[1] = 0;

for(long i=2;i<=sqrt(n);++i) {

if(!f[i]) continue;

for(long j=i*i;j<n;j+=i)

f[j] = 0;

}

int ans = accumulate(f.begin(), f.end(), 0);

return ans;

}

};

Java

// Author: Huahua

// Running time: 16 ms

class Solution {

public int countPrimes(int n) {

int ans = 0;

boolean[] isPrime = new boolean[n + 1];

Arrays.fill(isPrime, true);

isPrime[0] = false;

if (n > 0) isPrime[1] = false;

for (int i = 2; i < n; ++i) {

if (!isPrime[i]) continue;

++ans;

for (int j = 2 * i; j < n; j += i)

isPrime[j] = false;

}

return ans;

}

Python3

"""

Author: Huahua

Running time: 800 ms

"""

class Solution:

def countPrimes(self, n):

if n < 3: return 0

isPrime = [True] * (n + 1)

isPrime[0] = False

isPrime[1] = False

ans = 0

for i in range(2, n):

if not isPrime[i]: continue

ans += 1

for j in range(2 * i, n, i):

isPrime[j] = False

return ans

花花酱 LeetCode 241. Different Ways to Add Parentheses

By zxi on September 3, 2017

Given a string of numbers and operators, return all possible results from computing all the different possible ways to group numbers and operators. The valid operators are +, - and *.

Example 1:

Input: "2-1-1".

1 2	((2-1)-1) = 0 (2-(1-1)) = 2

Output: [0, 2]

Example 2:

Input: "2*3-4*5"

(2*(3-(4*5))) = -34

((2*3)-(4*5)) = -14

((2*(3-4))*5) = -10

(2*((3-4)*5)) = -10

(((2*3)-4)*5) = 10

Output: [-34, -14, -10, -10, 10]

Solution:

Running time: 3ms

C++

// Author: Huahua

namespace huahua {

int add(int a, int b) { return a+b; }

int minus(int a, int b) { return a-b; }

int multiply(int a, int b) { return a*b; }

} // namespace huahua

class Solution {

public:

vector<int> diffWaysToCompute(string input) {

return ways(input);

}

private:

const vector<int>& ways(const string& input) {

// Already solved, return the answer

if(m_.count(input)) return m_[input];

// Array for answer of input

vector<int> ans;

// Break the expression at every operator

for(int i=0;i<input.length();++i) {

char op = input[i];

// Split the input by an op

if(op=='+' || op=='-' || op=='*') {

const string left = input.substr(0, i);

const string right = input.substr(i+1);

// Get the solution of left/right sub-expressions

const vector<int>& l = ways(left);

const vector<int>& r = ways(right);

std::function<int(int,int)> f;

switch(op) {

case '+': f = huahua::add; break;

case '-': f = huahua::minus; break;

case '*': f = huahua::multiply; break;

}

// Combine the solution

for(int a : l)

for(int b : r)

ans.push_back(f(a,b));

}

// Single number, e.g. s = "3"

if(ans.empty())

ans.push_back(std::stoi(input));

// memorize the answer for input

m_[input].swap(ans);

return m_[input];

}

unordered_map<string, vector<int>> m_;

};

Python3

# Author: Huahua, 44 ms

class Solution:

def diffWaysToCompute(self, input):

ops = {'+': lambda x, y: x + y,

'-': lambda x, y: x - y,

'*': lambda x, y: x * y}

def ways(s):

ans = []

for i in range(len(s)):

if s[i] in "+-*":

ans += [ops[s[i]](l, r) for l, r in itertools.product(ways(s[0:i]), ways(s[i+1:]))]

if not ans: ans.append(int(s))

return ans

return ways(input)