Posts tagged as “medium”

花花酱 LeetCode 2055. Plates Between Candles

By zxi on November 3, 2021

There is a long table with a line of plates and candles arranged on top of it. You are given a 0-indexed string s consisting of characters '*' and '|' only, where a '*' represents a plate and a '|' represents a candle.

You are also given a 0-indexed 2D integer array queries where queries[i] = [left_i, right_i] denotes the substring s[left_i...right_i] (inclusive). For each query, you need to find the number of plates between candles that are in the substring. A plate is considered between candles if there is at least one candle to its left and at least one candle to its right in the substring.

For example, s = "||**||**|*", and a query [3, 8] denotes the substring "*||**|". The number of plates between candles in this substring is 2, as each of the two plates has at least one candle in the substring to its left and right.

Return an integer array answer where answer[i] is the answer to the i^th query.

Example 1:

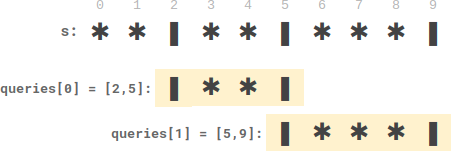
Input: s = "**|**|***|", queries = [[2,5],[5,9]]
Output: [2,3]
Explanation:
- queries[0] has two plates between candles.
- queries[1] has three plates between candles.

Example 2:

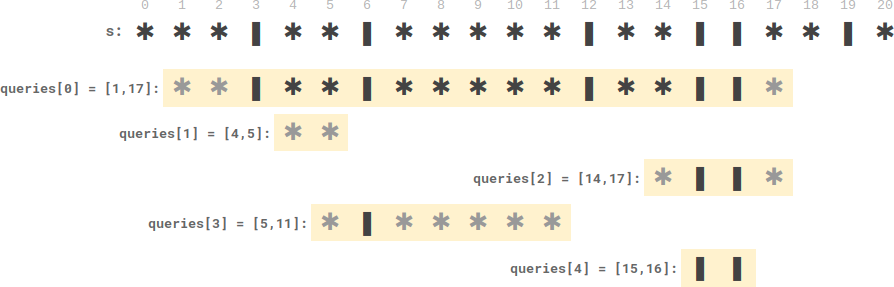
Input: s = "***|**|*****|**||**|*", queries = [[1,17],[4,5],[14,17],[5,11],[15,16]]
Output: [9,0,0,0,0]
Explanation:
- queries[0] has nine plates between candles.
- The other queries have zero plates between candles.

Constraints:

3 <= s.length <= 10⁵
s consists of '*' and '|' characters.
1 <= queries.length <= 10⁵
queries[i].length == 2
0 <= left_i <= right_i < s.length

Solution: Binary Search

Store the indices of all candles into an array idx.

For each query q:
1. Find the left most candle whose index is greater or equal to left as l.
2. Find the left most candle whose index is greater than right, choose the previous candle as r.

[idx[l], idx[r]] is the range that are elements between two candles , there are (idx[r] – idx[l] + 1) elements in total and there are (r – l + 1) candles in the range. So the number of plates is (idx[r] – idx[l] + 1) – (r – l + 1) or (idx[r] – idx[l]) – (r – l)

Time complexity: O(qlogn)
Space complexity: O(n)

C++

// Author: huahua

class Solution {

public:

vector<int> platesBetweenCandles(string s, vector<vector<int>>& queries) {

vector<int> idx;

for (size_t i = 0; i < s.size(); ++i)

if (s[i] == '|') idx.push_back(i);

vector<int> ans;

for (const auto& q : queries) {

const int l = lower_bound(begin(idx), end(idx), q[0]) - begin(idx);

const int r = upper_bound(begin(idx), end(idx), q[1]) - begin(idx) - 1;

ans.push_back(l >= r ? 0 : (idx[r] - idx[l]) - (r - l));

}

return ans;

}

};

花花酱 LeetCode 2054. Two Best Non-Overlapping Events

By zxi on November 1, 2021

You are given a 0-indexed 2D integer array of events where events[i] = [startTime_i, endTime_i, value_i]. The i^th event starts at startTime_iand ends at endTime_i, and if you attend this event, you will receive a value of value_i. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.

Return this maximum sum.

Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.

Example 1:

Input: events = [[1,3,2],[4,5,2],[2,4,3]]
Output: 4
Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.

Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]]
Output: 5
Explanation: Choose event 2 for a sum of 5.

Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]
Output: 8
Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.

Constraints:

2 <= events.length <= 10⁵
events[i].length == 3
1 <= startTime_i <= endTime_i <= 10⁹
1 <= value_i <= 10⁶

Solution: Sort + Heap

Sort events by start time, process them from left to right.

Use a min heap to store the events processed so far, a variable cur to track the max value of a non-overlapping event.

For a given event, pop all non-overlapping events whose end time is smaller than its start time and update cur.

ans = max(val + cur)

Time complexity: O(nlogn)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int maxTwoEvents(vector<vector<int>>& events) {

using E = pair<int,int>;

sort(begin(events), end(events));

priority_queue<E, vector<E>, greater<E>> q; // (end_time, val)

int ans = 0;

int cur = 0;

for (const auto& e : events) {

while (!q.empty() && q.top().first < e[0]) {

cur = max(cur, q.top().second);

q.pop();

}

ans = max(ans, cur + e[2]);

q.emplace(e[1], e[2]);

}

return ans;

}

};

花花酱 LeetCode 2049. Count Nodes With the Highest Score

By zxi on October 26, 2021

There is a binary tree rooted at 0 consisting of n nodes. The nodes are labeled from 0 to n - 1. You are given a 0-indexed integer array parents representing the tree, where parents[i] is the parent of node i. Since node 0 is the root, parents[0] == -1.

Each node has a score. To find the score of a node, consider if the node and the edges connected to it were removed. The tree would become one or more non-empty subtrees. The size of a subtree is the number of the nodes in it. The score of the node is the product of the sizes of all those subtrees.

Return the number of nodes that have the highest score.

Example 1:

Input: parents = [-1,2,0,2,0]
Output: 3
Explanation:
- The score of node 0 is: 3 * 1 = 3
- The score of node 1 is: 4 = 4
- The score of node 2 is: 1 * 1 * 2 = 2
- The score of node 3 is: 4 = 4
- The score of node 4 is: 4 = 4
The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.

Example 2:

Input: parents = [-1,2,0]
Output: 2
Explanation:
- The score of node 0 is: 2 = 2
- The score of node 1 is: 2 = 2
- The score of node 2 is: 1 * 1 = 1
The highest score is 2, and two nodes (node 0 and node 1) have the highest score.

Constraints:

n == parents.length
2 <= n <= 10⁵
parents[0] == -1
0 <= parents[i] <= n - 1 for i != 0
parents represents a valid binary tree.

Solution: Recursion

Write a function that returns the element of a subtree rooted at node.

We can compute the score based on:
1. size of the subtree(s)
2. # of children

Root is a special case whose score is max(c[0], 1) * max(c[1], 1).

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

int countHighestScoreNodes(vector<int>& parents) {

const int n = parents.size();

long high = 0;

int ans = 0;

vector<vector<int>> tree(n);

for (int i = 1; i < n; ++i)

tree[parents[i]].push_back(i);

function<int(int)> dfs = [&](int node) -> int {

long c[2] = {0, 0};

for (int i = 0; i < tree[node].size(); ++i)

c[i] = dfs(tree[node][i]);

long score = 0;

if (node == 0) // case #1: root

score = max(c[0], 1l) * max(c[1], 1l);

else if (tree[node].size() == 0) // case #2: leaf

score = n - 1;

else if (tree[node].size() == 1) // case #3: one child

score = c[0] * (n - c[0] - 1);

else // case #4: two children

score = c[0] * c[1] * (n - c[0] - c[1] - 1);

if (score > high) {

high = score;

ans = 1;

} else if (score == high) {

++ans;

}

return 1 + c[0] + c[1];

};

dfs(0);

return ans;

}

};

花花酱 LeetCode 2048. Next Greater Numerically Balanced Number

By zxi on October 25, 2021

An integer x is numerically balanced if for every digit d in the number x, there are exactly d occurrences of that digit in x.

Given an integer n, return the smallest numerically balanced number strictly greater than n.

Example 1:

Input: n = 1
Output: 22
Explanation: 
22 is numerically balanced since:
- The digit 2 occurs 2 times. 
It is also the smallest numerically balanced number strictly greater than 1.

Example 2:

Input: n = 1000
Output: 1333
Explanation: 
1333 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times. 
It is also the smallest numerically balanced number strictly greater than 1000.
Note that 1022 cannot be the answer because 0 appeared more than 0 times.

Example 3:

Input: n = 3000
Output: 3133
Explanation: 
3133 is numerically balanced since:
- The digit 1 occurs 1 time.
- The digit 3 occurs 3 times.
It is also the smallest numerically balanced number strictly greater than 3000.

Constraints:

0 <= n <= 10⁶

Solution: Permutation

Time complexity: O(log(n)!)
Space complexity: O(log(n)) ?

C++

// Author: Huahua

class Solution {

public:

int nextBeautifulNumber(int n) {

const string t = to_string(n);

vector<int> nums{1,

22,

122, 333,

1333, 4444,

14444, 22333, 55555,

122333, 155555, 224444, 666666};

int ans = 1224444;

for (int num : nums) {

string s = to_string(num);

if (s.size() < t.size()) continue;

else if (s.size() > t.size()) {

ans = min(ans, num);

} else { // same length

do {

if (s > t) ans = min(ans, stoi(s));

} while (next_permutation(begin(s), end(s)));

}

return ans;

}

};

LeetCode 2033. Minimum Operations to Make a Uni-Value Grid

By zxi on October 21, 2021

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

Example 1:

Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.

Example 2:

Input: grid = [[1,5],[2,3]], x = 1
Output: 5
Explanation: We can make every element equal to 3.

Example 3:

Input: grid = [[1,2],[3,4]], x = 2
Output: -1
Explanation: It is impossible to make every element equal.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
1 <= x, grid[i][j] <= 10⁴

Solution: Median

To achieve minimum operations, the uni-value must be the median of the array.

Time complexity: O(m*n)
Space complexity: O(m*n)

C++

// Author; Huahua

class Solution {

public:

int minOperations(vector<vector<int>>& grid, int x) {

const int mn = grid.size() * grid[0].size();

vector<int> nums;

nums.reserve(mn);

for (const auto& row : grid)

nums.insert(end(nums), begin(row), end(row));

nth_element(begin(nums), begin(nums) + mn / 2, end(nums));

const int median = nums[mn / 2];

int ans = 0;

for (int v : nums) {

if (abs(v - median) % x) return -1;

ans += abs(v - median) / x;

}

return ans;

}

};