There is a binary tree rooted at 0 consisting of n nodes. The nodes are labeled from 0 to n - 1. You are given a 0-indexed integer array parents representing the tree, where parents[i] is the parent of node i. Since node 0 is the root, parents[0] == -1.
Each node has a score. To find the score of a node, consider if the node and the edges connected to it were removed. The tree would become one or more non-empty subtrees. The size of a subtree is the number of the nodes in it. The score of the node is the product of the sizes of all those subtrees.
Return the number of nodes that have the highest score.
Example 1:
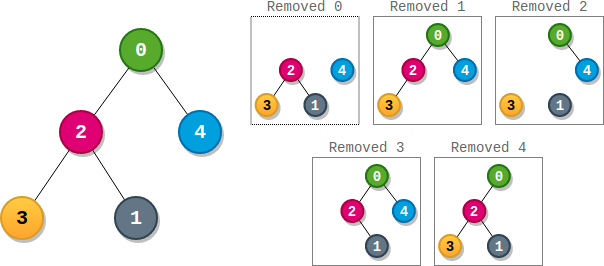
Input: parents = [-1,2,0,2,0] Output: 3 Explanation: - The score of node 0 is: 3 * 1 = 3 - The score of node 1 is: 4 = 4 - The score of node 2 is: 1 * 1 * 2 = 2 - The score of node 3 is: 4 = 4 - The score of node 4 is: 4 = 4 The highest score is 4, and three nodes (node 1, node 3, and node 4) have the highest score.
Example 2:
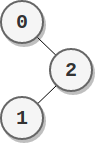
Input: parents = [-1,2,0] Output: 2 Explanation: - The score of node 0 is: 2 = 2 - The score of node 1 is: 2 = 2 - The score of node 2 is: 1 * 1 = 1 The highest score is 2, and two nodes (node 0 and node 1) have the highest score.
Constraints:
n == parents.length2 <= n <= 105parents[0] == -10 <= parents[i] <= n - 1fori != 0parentsrepresents a valid binary tree.
Solution: Recursion
Write a function that returns the element of a subtree rooted at node.
We can compute the score based on:
1. size of the subtree(s)
2. # of children
Root is a special case whose score is max(c[0], 1) * max(c[1], 1).
Time complexity: O(n)
Space complexity: O(n)
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
// Author: Huahua class Solution { public: int countHighestScoreNodes(vector<int>& parents) { const int n = parents.size(); long high = 0; int ans = 0; vector<vector<int>> tree(n); for (int i = 1; i < n; ++i) tree[parents[i]].push_back(i); function<int(int)> dfs = [&](int node) -> int { long c[2] = {0, 0}; for (int i = 0; i < tree[node].size(); ++i) c[i] = dfs(tree[node][i]); long score = 0; if (node == 0) // case #1: root score = max(c[0], 1l) * max(c[1], 1l); else if (tree[node].size() == 0) // case #2: leaf score = n - 1; else if (tree[node].size() == 1) // case #3: one child score = c[0] * (n - c[0] - 1); else // case #4: two children score = c[0] * c[1] * (n - c[0] - c[1] - 1); if (score > high) { high = score; ans = 1; } else if (score == high) { ++ans; } return 1 + c[0] + c[1]; }; dfs(0); return ans; } }; |
请尊重作者的劳动成果,转载请注明出处!花花保留对文章/视频的所有权利。
如果您喜欢这篇文章/视频,欢迎您捐赠花花。
If you like my articles / videos, donations are welcome.



Be First to Comment