Posts tagged as “probability”

花花酱 LeetCode 1467. Probability of a Two Boxes Having The Same Number of Distinct Balls

By zxi on June 3, 2020

Given 2n balls of k distinct colors. You will be given an integer array balls of size k where balls[i] is the number of balls of color i.

All the balls will be shuffled uniformly at random, then we will distribute the first n balls to the first box and the remaining n balls to the other box (Please read the explanation of the second example carefully).

Please note that the two boxes are considered different. For example, if we have two balls of colors a and b, and two boxes [] and (), then the distribution [a] (b) is considered different than the distribution [b] (a) (Please read the explanation of the first example carefully).

We want to calculate the probability that the two boxes have the same number of distinct balls.

Example 1:

Input: balls = [1,1]
Output: 1.00000
Explanation: Only 2 ways to divide the balls equally:
- A ball of color 1 to box 1 and a ball of color 2 to box 2
- A ball of color 2 to box 1 and a ball of color 1 to box 2
In both ways, the number of distinct colors in each box is equal. The probability is 2/2 = 1

Example 2:

Input: balls = [2,1,1]
Output: 0.66667
Explanation: We have the set of balls [1, 1, 2, 3]
This set of balls will be shuffled randomly and we may have one of the 12 distinct shuffles with equale probability (i.e. 1/12):
[1,1 / 2,3], [1,1 / 3,2], [1,2 / 1,3], [1,2 / 3,1], [1,3 / 1,2], [1,3 / 2,1], [2,1 / 1,3], [2,1 / 3,1], [2,3 / 1,1], [3,1 / 1,2], [3,1 / 2,1], [3,2 / 1,1]
After that we add the first two balls to the first box and the second two balls to the second box.
We can see that 8 of these 12 possible random distributions have the same number of distinct colors of balls in each box.
Probability is 8/12 = 0.66667

Example 3:

Input: balls = [1,2,1,2]
Output: 0.60000
Explanation: The set of balls is [1, 2, 2, 3, 4, 4]. It is hard to display all the 180 possible random shuffles of this set but it is easy to check that 108 of them will have the same number of distinct colors in each box.
Probability = 108 / 180 = 0.6

Example 4:

Input: balls = [3,2,1]
Output: 0.30000
Explanation: The set of balls is [1, 1, 1, 2, 2, 3]. It is hard to display all the 60 possible random shuffles of this set but it is easy to check that 18 of them will have the same number of distinct colors in each box.
Probability = 18 / 60 = 0.3

Example 5:

Input: balls = [6,6,6,6,6,6]
Output: 0.90327

Constraints:

1 <= balls.length <= 8
1 <= balls[i] <= 6
sum(balls) is even.
Answers within 10^-5 of the actual value will be accepted as correct.

Solution 0: Permutation (TLE)

Enumerate all permutations of the balls, count valid ones and divide that by the total.

Time complexity: O((8*6)!) = O(48!)
After deduplication: O(48!/(6!)^8) ~ 1.7e38
Space complexity: O(8*6)

C++

// Author: Huahua, TLE 4/21 passed

class Solution {

public:

double getProbability(vector<int>& balls) {

const int k = balls.size();

vector<int> bs;

for (int i = 0; i < k; ++i)

for (int j = 0; j < balls[i]; ++j)

bs.push_back(i);

const int n = bs.size();

double total = 0.0;

double valid = 0.0;

// d : depth

// used : bitmap of bs's usage

// c1: bitmap of colors of box1

// c2: bitmap of colors of box1

function<void(int, long, int, int)> dfs = [&](int d, long used, int c1, int c2) {

if (d == n) {

total += 1;

valid += __builtin_popcount(c1) == __builtin_popcount(c2);

return;

}

for (int i = 0; i < n; ++i) {

if (used & (1L << i)) continue;

// Deduplication.

if (i > 0 && bs[i] == bs[i - 1] && !(used & (1L << (i - 1)))) continue;

int tc1 = (d < n / 2) ? (c1 | (1 << bs[i])) : c1;

int tc2 = (d < n / 2) ? c2 : (c2 | (1 << bs[i]));

dfs(d + 1, used | (1L << i), tc1, tc2);

}

};

dfs(0, 0, 0, 0);

return valid / total;

}

};

Solution 1: Combination

For each color, put n_i balls into box1, the left t_i – n_i balls go to box2.
permutations = fact(n//2) / PROD(fact(n_i)) * fact(n//2) * PROD(fact(t_i – n_i))
E.g
balls = [1×2, 2×6, 3×4]
One possible combination:
box1: 1 22 333
box2: 1 2222 3
permutations = 6! / (1! * 2! * 3!) * 6! / (1! * 4! * 1!) = 1800

Time complexity: O((t+1)^k) = O(7^8)
Space complexity: O(k + (t*k)) = O(8 + 48)

C++

// Author: Huahua

class Solution {

public:

double getProbability(vector<int>& balls) {

const int n = accumulate(begin(balls), end(balls), 0);

const int k = balls.size();

double total = 0.0;

double valid = 0.0;

vector<double> fact(50, 1.0);

for (int i = 1; i < fact.size(); ++i)

fact[i] = fact[i - 1] * i;

// d: depth

// b1, b2: # of balls in box1, box2

// c1, c2: # of distinct colors in box1, box2

// p1, p2: # permutations of duplicate balls in box1, box2

function<void(int, int, int, int, int, double, double)> dfs = [&]

(int d, int b1, int b2, int c1, int c2, double p1, double p2) {

if (b1 > n / 2 || b2 > n / 2) return;

if (d == k) {

const double count = fact[b1] / p1 * fact[b2] / p2;

total += count;

valid += count * (c1 == c2);

return;

}

for (int s1 = 0; s1 <= balls[d]; ++s1) {

const int s2 = balls[d] - s1;

dfs(d + 1,

b1 + s1,

b2 + s2,

c1 + (s1 > 0),

c2 + (s2 > 0),

p1 * fact[s1],

p2 * fact[s2]);

}

};

dfs(0, 0, 0, 0, 0, 1.0, 1.0);

return valid / total;

}

};

vector version

C++

// Author: Huahua

class Solution {

public:

double getProbability(vector<int>& balls) {

const int k = balls.size();

const int n = accumulate(begin(balls), end(balls), 0);

vector<double> fact(49, 1.0);

for (int i = 1; i < fact.size(); ++i)

fact[i] = fact[i - 1] * i;

auto perms = [&](const vector<int>& bs, int n) -> double {

double p = fact[n];

for (int b : bs) p /= fact[b];

return p;

};

vector<int> box1, box2;

function<double(int)> dfs = [&](int d) -> double {

const int n1 = accumulate(begin(box1), end(box1), 0);

const int n2 = accumulate(begin(box2), end(box2), 0);

if (n1 > n / 2 || n2 > n / 2) return 0;

if (d == k)

return (box1.size() == box2.size()) * perms(box1, n1) * perms(box2, n2);

double total = 0;

for (int s1 = 0; s1 <= balls[d]; ++s1) {

const int s2 = balls[d] - s1;

if (s1) box1.push_back(s1);

if (s2) box2.push_back(s2);

total += dfs(d + 1);

if (s1) box1.pop_back();

if (s2) box2.pop_back();

}

return total;

};

return dfs(0) / perms(balls, n);

}

};

花花酱 LeetCode 1377. Frog Position After T Seconds

By zxi on March 8, 2020

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [from_i, to_i] means that exists an edge connecting directly the vertices from_i and to_i.

Return the probability that after t seconds the frog is on the vertex target.

Example 1:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.

Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.

Example 3:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

1 <= n <= 100
edges.length == n-1
edges[i].length == 2
1 <= edges[i][0], edges[i][1] <= n
1 <= t <= 50
1 <= target <= n
Answers within 10^-5 of the actual value will be accepted as correct.

Solution: BFS

key: if a node has children, the fog jumps to to children so the probability at current node will become 0.

Time complexity: O(n)
Space complexity: O(n)

C++

// Author: Huahua

class Solution {

public:

double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {

vector<double> p(n + 1);

p[1] = 1.0;

vector<vector<int>> g(n + 1);

for (const auto& e : edges) {

g[e[0]].push_back(e[1]);

g[e[1]].push_back(e[0]);

}

vector<int> seen(n + 1);

seen[1] = 1;

queue<int> q{{1}};

while (t--) {

int size = q.size();

while (size--) {

int cur = q.front(); q.pop();

int children = 0;

for (int nxt : g[cur])

if (!seen[nxt]) ++children;

for (int nxt : g[cur])

if (!seen[nxt]++) {

q.push(nxt);

p[nxt] += p[cur] / children;

}

// key: fog jumps this node has children

if (children > 0) p[cur] = 0.0;

}

return p[target];

}

};

python3

class Solution:

def frogPosition(self, n: int, edges: List[List[int]],

t: int, target: int) -> float:

p = [0] + [1] + [0] * (n - 1)

seen = [False] + [True] + [False] * (n - 1)

q = [1]

g = [[] for _ in range(n + 1)]

for i, j in edges:

g[i].append(j)

g[j].append(i)

for _ in range(t):

q2 = []

for cur in q:

children = sum([not seen[nxt] for nxt in g[cur]])

for nxt in g[cur]:

if seen[nxt]: continue

seen[nxt] = True

q2.append(nxt)

p[nxt] = p[cur] / children

if children > 0: p[cur] = 0

q = q2

return p[target]

花花酱 LeetCode 470. Implement Rand10() Using Rand7()

By zxi on October 15, 2018

Problem

Given a function rand7 which generates a uniform random integer in the range 1 to 7, write a function rand10 which generates a uniform random integer in the range 1 to 10.

Do NOT use system’s Math.random().

Example 1:

Input: 1
Output: [7]

Example 2:

Input: 2
Output: [8,4]

Example 3:

Input: 3
Output: [8,1,10]

Note:

rand7 is predefined.
Each testcase has one argument: n, the number of times that rand10 is called.

Follow up:

What is the expected value for the number of calls to rand7() function?
Could you minimize the number of calls to rand7()?

Solution:

Time complexity: O(1)

Space complexity: O(1)

C++

// Author: Huahua

class Solution {

public:

int rand10() {

int index = INT_MAX;

while (index >= 40)

index = 7 * (rand7() - 1) + (rand7() - 1);

return index % 10 + 1;

}

};

花花酱 LeetCode 808. Soup Servings

By zxi on August 1, 2018

Problem

There are two types of soup: type A and type B. Initially we have N ml of each type of soup. There are four kinds of operations:

Serve 100 ml of soup A and 0 ml of soup B
Serve 75 ml of soup A and 25 ml of soup B
Serve 50 ml of soup A and 50 ml of soup B
Serve 25 ml of soup A and 75 ml of soup B

When we serve some soup, we give it to someone and we no longer have it. Each turn, we will choose from the four operations with equal probability 0.25. If the remaining volume of soup is not enough to complete the operation, we will serve as much as we can. We stop once we no longer have some quantity of both types of soup.

Note that we do not have the operation where all 100 ml’s of soup B are used first.

Return the probability that soup A will be empty first, plus half the probability that A and B become empty at the same time.

Example:
Input: N = 50
Output: 0.625
Explanation: 
If we choose the first two operations, A will become empty first. For the third operation, A and B will become empty at the same time. For the fourth operation, B will become empty first. So the total probability of A becoming empty first plus half the probability that A and B become empty at the same time, is 0.25 * (1 + 1 + 0.5 + 0) = 0.625.

Notes:

0 <= N <= 10^9.
Answers within 10^-6 of the true value will be accepted as correct.

Solution 1: Recursion with Memorization

Time complexity: O(N^2) N ~ 5000 / 25 = 200

Space complexity: O(N^2)

C++

// Author: Huahua

// Running time: 4 ms

class Solution {

public:

double soupServings(int N) {

if (N >= 5000) return 1.0;

return prob(N, N);

}

private:

unordered_map<int, unordered_map<int, double>> m_;

double prob(int A, int B) {

static int ops[][2] = {{100, 0}, {75, 25}, {50, 50}, {25, 75}};

if (A <= 0 && B <= 0) return 0.5;

if (A <= 0) return 1.0;

if (B <= 0) return 0.0;

if (m_.count(A) && m_[A].count(B)) return m_[A][B];

m_[A][B] = 0.0;

for (int i = 0; i < 4; ++i)

m_[A][B] += 0.25 * prob(A - ops[i][0], B - ops[i][1]);

return m_[A][B];

}

};

花花酱 688. Knight Probability in Chessboard

By zxi on October 1, 2017

https://leetcode.com/problems/knight-probability-in-chessboard/description/

Problem:

On an NxN chessboard, a knight starts at the r-th row and c-th column and attempts to make exactly Kmoves. The rows and columns are 0 indexed, so the top-left square is (0, 0), and the bottom-right square is (N-1, N-1).

A chess knight has 8 possible moves it can make, as illustrated below. Each move is two squares in a cardinal direction, then one square in an orthogonal direction.

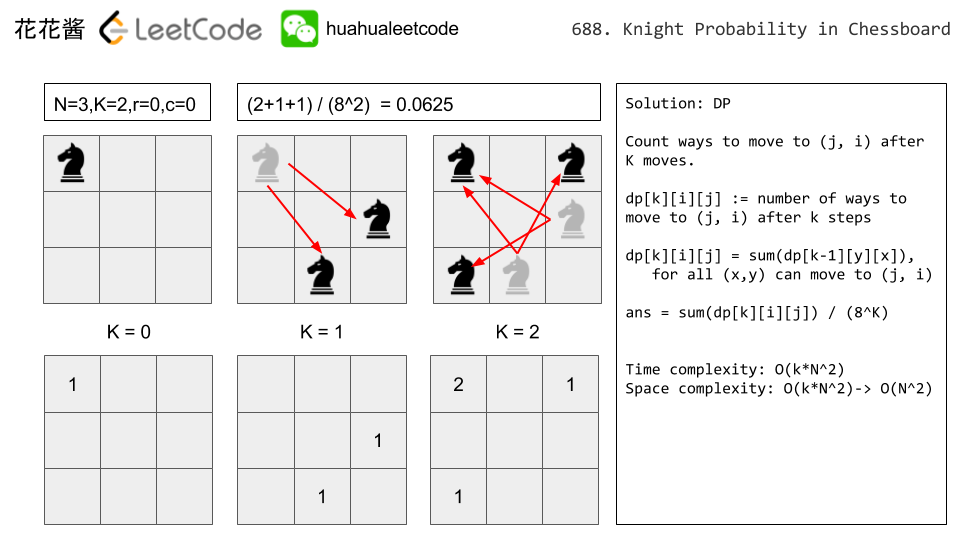
Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.

The knight continues moving until it has made exactly K moves or has moved off the chessboard. Return the probability that the knight remains on the board after it has stopped moving.

Example:

Input: 3, 2, 0, 0

Output: 0.0625

Explanation: There are two moves (to (1,2), (2,1)) that will keep the knight on the board.

From each of those positions, there are also two moves that will keep the knight on

the board. The total probability the knight stays on the board is 0.0625.

Note:

N will be between 1 and 25.
K will be between 0 and 100.
The knight always initially starts on the board.

Idea:

Dynamic programming

Count the ways to reach (x, y) after k moves from start.

Time Complexity: O(k*n^2)

Space Complexity: O(n^2)

Solution:

// Author: Huahua

// Runtime: 6 ms

class Solution {

public:

double knightProbability(int N, int K, int r, int c) {

vector<vector<double>> dp0(N, vector<double>(N, 0.0));

dp0[r][c] = 1.0;

int dirs[8][2] = {{1, 2}, {-1, -2}, {1, -2}, {-1, 2},

{2, 1}, {-2, -1}, {2, -1}, {-2, 1}};

for (int k = 0; k < K; ++k) {

vector<vector<double>> dp1(N, vector<double>(N, 0.0));

for (int i = 0; i < N; ++i)

for (int j = 0; j < N; ++j)

for (int m = 0; m < 8; ++m) {

int x = j + dirs[m][0];

int y = i + dirs[m][1];

if (x < 0 || y < 0 || x >= N || y >= N) continue;

dp1[i][j] += dp0[y][x];

}

std::swap(dp0, dp1);

}

double total = 0;

for (int i = 0; i < N; ++i)

for (int j = 0; j < N; ++j)

total += dp0[i][j];

return total / pow(8, K);

}

};

Related problems: